偏波
|
|
|
- つかさ さんきち
- 5 years ago
- Views:
Transcription
1 の基礎. の表現方法 とは, 図.に示すように空間のある定まった位置で, 単一周波数の電波を進行方向の後ろ側から眺めたとき, 時間と共に電界ベクトルの先端が描く軌跡のことである. 電界ベクトルの先端の軌跡は, 一般的にだ円形となることが知られている. だ円の中には扁平なだ円, 円に近いだ円, 傾いただ円など様々なものが含まれる. 扁平の極限として直線や円がある. また, 軌跡の回転方向もある. これら種々のだ円を表わすのに,ellipticit angle,tilt angle,size, 相対位相, 比, ストークスパラメータ, ポアンカレ球 (Poincare Sphere) などが用いられている. この節では, だ円を表現する際に使われるいくつかの記号と, その定義およびそれらの関係を紹介する. 重複になるが, は電界ベクトルそのものではなく, ベクトル先端の軌跡である. だ円形の電界ベクトル? というような間違いをしないように注意が必要である. 電界ベクトル先端の軌跡 進行方向 瞬時電界の向き 軌跡 拡大 Transverse 面 Transverse 面で見えるいろいろな軌跡 状態 図. 電界の先端の軌跡. 一般的数式表現 平面波の電界は, 横断面 (Transverse 面 ) 内で つの直交成分に分解できる. この波が +z 方向に伝搬す ると仮定して,-の直交成分に分解してみよう.z 方向に伝搬する場合, 電界のz 方向成分は存在しない. 瞬時電界ベクトルε ( z, t ) は実数であり, 次のように書くことができる. ε ( z, t ) ε ( z, t ) ε ( z, t ) cos ( ω t - k z + φ ) cos ( ω t - k z + φ ) (.) ここで,, は振幅,φ,φ は絶対位相を表わす. の定義に従って z の定位置で観測した とすると, 式 (.) は ε (, t ) ε ( t ) として ε ( t ) ε ( t ) ε ( t ) cos ( ω t + φ ) cos ( ω t + φ ) (.) /
2 となる. 各成分は ε ( t ) cos (ω t + φ ) cos ω t cos φ - sin ω t sin φ ε ( t ) cos (ω t + φ ) cos ω t cos φ - sin ω t sin φ (.3) である. 相対位相差を δ φ - φ (.4) とおいて, 式 (.3) を変形すると ε (t) cos φ ε (t) cos φ sin δ sin ω t ε (t) sin φ ε (t) sin φ sin δ cos ω t (.5) が得られる. これから sin ω t + cos ω t を使って時間因子 ω t の項を消去すると次式が得られる. ε (t) ε (t) ε (t) cos δ + ε (t) sin δ (.6) この式は傾きをもつだ円の方程式である.δ が特別の値のときは分かり易い式に帰着する. 例えば, a, b, ε (t), ε (t) とおくと, 次の方程式になる. a a b cos δ + b sin δ δ ± π のとき a + : 傾きのないだ円の方程式 b さらに a b なら + a : 円の方程式 δ, π のとき a + a b + b a + b, ± b a : 直線の方程式 それゆえ, 瞬時電界ベクトル ε ( t ) は, 図. に示すようなだ円の軌跡を描くことがわかる. 電界ベクトル ε ( t ) の回転方向は位相の時間変化によって分かる. 図. のように 軸と ε ( t ) のなす角を ψ とすると ε ε ( t) Ψ z ε 図. 電界ベクトル先端の軌跡 /
3 その時間変化は微分操作より, tan ψ ε (t) ε (t) (.7) dψ dt ω sin δ ω sin δ (.8) E cos ω t + φ + E cos ω t + φ ε これより, 図. を参照して < δ < π に対して π < δ < に対して dψ dt dψ dt < ( 時計回り ) (.9a) > ( 反時計回り ) (.9b) となる. 図.3に時間と共に変化する位相角の方向を示す. 図.3(a) と図.の直角座標系 - 平面では,z 軸は紙面から読者側に向き, 電波は正のz 方向に進むと仮定しているので, 電波の到来方向から見ていることになる. また, 図.3(b) は後ろ側から見た図である. d Ψ dt < d Ψ dt < (a) 到来方向から見た図 (b) 進行方向後ろから見た図 図.3 回転の方向 ( 左回り ) 回転方向の定義は, 伝搬方向の後ろ側から電界ベクトルの先端を見たときに, 時間の経過と共にどちらの方向に回るかで決めている.IEEE Standard [7] によれば,z 一定の面内で, 時間と共に時計回りに回転するものを 右回り と定義し, 反時計回りに回転するものを 左回り と定義している. 図.3(a) のように 到来方向から見た場合は, dψ dt < は時計回りで, 一見すると右回りに思えるが, 電波を見る方向が逆なの で, 図.3(b) のように左回りである. また, dψ > dt の場合が右回りである. 以上のことから, 電界の回転方向は相対位相 δ φ - φ の符号によって区別できる. < δ < π ならば左回り (Left handed rotation sense) π < δ < ならば右回り (Right handed rotation sense) 図.4 に δ と共に一般的なだ円を示した. 状態を表す電界の具体的表現は次のようになる. 簡単のた めに,φ とおき,δ φ - φ φ としている. 一般形 ε ( z, t ) cos ( ω t - k z ) ε ( z, t ) cos ( ω t - k z + δ ), ならば水平 ε ( z, t ) cos ( ω t - k z ) ε ( z, t ) 3/
4 left handed rotation π > δ > π δ π π > δ > δ φ φ z z δ ± π δ π < δ < π δ π π < δ < right handed rotation 図.4 一般的なだ円, ならば垂直 ε ( z, t ) ε ( z, t ) cos ( ω t - k z + δ ), の場合, δ δ π ならば ε ( z, t ) と ε ( z, t ) が同相なので, 正に傾いた直線 ならば ε ( z, t ) と ε ( z, t ) が逆相なので, 負に傾いた直線 < δ < π は左回りだ円 さらに, もし δ π, ならば, 左回り円 ε ( z, t ) cos ( ω t - k z ) ε ( z, t ) sin ( ω t k z ) ψѱ ω t π < δ < は右回りだ円 さらに, もし δ π, ならば, 右回り円 ε ( z, t ) cos ( ω t - k z ) ε ( z, t ) sin ( ω t k z ) ψѱ ω t したがって, 直線も円も, だ円の中の特別な状態であることが分かる. 4/
5 . 幾何学的パラメータによる表現 だ円を表現するのには, 幾何学的パラメータ ( τ, ε, A ) を使うほうが直観的に分かりやすい. 幾何学的パラ メータは,ellipticit angle ε, 傾き角 (tilt angle) τ,size A である. はだ円を図.5 の目玉のように後 ろ側から見ることになっており, ε と τ は図.5, 図.6 に示す角度である. ε + ε τ z 図.5 座標系と幾何学的パラメータ ( τ, ε, A ) η A ε ξ b τ a z 図.6 だ円を表すパラメータ ( τ, ε, A ) Ellipticit angle ε ε tan - b a, tan ε b a π 4 ε π 4 (.) a はだ円の長軸,b はだ円の短軸の長さである.Ellipticit はだ円の膨らみ具合を表しており,tan ε はアンテ ナ工学で使う 軸比 の逆数である.a b では ε ± π 4 となって完全な円を表し,b では ε となるの 5/
6 で直線となる. 符号は回転の向きに対応しており, 左回りだ円に対しては ε >, 右回りだ円に対しては ε < となる. 後述の式 (.9) を参照. なお,ellipticit angle の記号 ε は頭文字に対応して採用した [4], [5], [9]. 誘電率と同じ記号なので混同しやすい面もあるが, 以後は特に断らない限り,ε をellipticit angleとして表すものする. Tilt angle ( 傾き角 ) τ は, だ円の長軸と 軸のなす角度であり, だ円の傾きを表す. その範囲は ( π τ π ) である. なお,Tilt angleの頭文字に対応して,τ の記号を採用しているが, 書物や文献によっては別の記号を使用したり,Orientation Angleと呼ぶことも多い. だ円の大きさは A a + b (.) によって与えられる.A は電力の大きさを表し, 情報とは直接関係しない. だ円は, 幾何学的パラメータ (Tilt angle, Ellipticit angle) によって図.7 のように一覧表で表現す ることができる.ε ± π 4 では, τ がどのような値になっても円である. 左回り 直線 右回り Tilt Angle (degree) 図.7 幾何学的パラメータによるだ円の表現 次に, 数式的なパラメータ (,, φ, φ ) と幾何学的パラメータ ( A, ε, τ ) の関係を求めてみよ う. 図.8において,ξ 軸とη 軸をそれぞれ長軸と短軸方向に選ぶ. この新しい座標系で, だ円は傾きのな い正規のだ円となる. この座標で電界の各成分は と書くことができる. ε ξ ε η a cos ω t + φ ξ b cos ω t + φ η (.a) 6/
7 η ε (t) ξ b φξ τ ε a ε ξ a 図.8 だ円の座標軸と電界成分 だ円の方程式 (.6) からも分かるように,ξ -η 軸に沿った正規のだ円では位相的には δ φ η φ ξ π となり, cos ωt + φ η sin ωt + φ ξ から次のように変形される. ただし,φ ξ は絶対位相であり, 図.8 に示すように 大きさの関係から a cos φ ξ ε ξ となる. ε ξ ε η a cos ω t + φ ξ b sin ω t + φ ξ (.b) 新しい ξ -η 軸は - 軸を τ だけ回転して得られるので, 電界は次のように変換できる. ε ξ ε η cos τ sin τ - sin τ cos τ ε ε (.3) 式 (.),(.) を式 (.3) に代入することによって a cos ω t + φ ξ cos ω t + φ cos τ + cos ω t + φ sin τ b sin ω t + φ ξ cos ω t + φ sin τ cos ω t + φ cos τ sin, cos 関数を展開し,sin ω t,cos ω t の係数を比較すれば a cos φ ξ cos φ cos τ + cos φ sin τ a sin φ ξ sin φ cos τ + sin φ sin τ b sin φ ξ cos φ sin τ cos φ cos τ b cos φ ξ sin φ sin τ sin φ cos τ (.4) 相対位相 δ φ φ を代入して整理すると, 次の関係式が得られる. 7/
8 a + b + ( エネルギ一定 ) (.5) ab sin φ φ sin δ (.6) sin τ cos τ cos δ (.7) したがって, 幾何学的パラメータとの関係は tan τ cos δ (.8) sin ε sin ε cos ε ab a + b sin δ (.9) + となる. また,(.b) から, ε ξ ε η a cos ω t + φ ξ a + b b sin ω t + φ ξ a a + b cos ω t + φ ξ b a + b sin ω t + φ ξ (.) (.3) より, A ε ε cos ε cos ω t + φ ξ sin ε sin ω t + φ ξ Re A cos τ sin τ sin τ cos τ ε ξ ε η Re A cos ε sin ε ep ω t + φ ξ cos τ sin τ sin τ cos τ cos ε sin ε ep ω t + φ ξ ε ε Re e φ e φ ep ω t だから,(,, φ, φ ) と ( A, ε, τ ) の関係は次のように なる. e φ e φ A cos τ sin τ sin τ cos τ cos ε sin ε e φ ξ (.) この式からベクトル cos ε sin ε e φ ξ を τ だけ回転させたものに等しいと解釈できる. ここで,(.) の位相関係を調べておこう.φ φ ξ φ とおいて変形すると e δ A cos τ sin τ sin τ cos τ cos ε sin ε e φ ξ φ A cos τ cos ε sinτ sin ε sinτ cos ε + cos τ sin ε e φ このベクトルの 行目は実数なので, その位相は とおくことができる. Arg cos τ cos ε sinτ sin ε + φ (.) したがって φ tan tan τ tan ε (.3) 8/
9 それゆえ, e δ A cos τ sin τ sin τ cos τ cos ε sin ε e tan tan τ tan ε (.4) と書くこともできる..3 ジョーンズベクトルによる表現 ここではフェーザを用いたベクトルで電界を表現する. 式 (.) のように E は複素振幅をもつ二次元ベク トルであり, 次の形で書ける. E e φ e φ (.5) このベクトルは " ジョーンズ (Jones) ベクトル " と呼ばれている. 成分を実数化するように相対位相を使うと (.4) の形になる. E e δ (.6) ジョーンズベクトルによるいくつかの状態を図.9 に示す. H τ ε z H V τ π ε V cos θ sin θ θ z τ θ ε 水平垂直傾いた直線 τ θ + π ε - sin θ cos θ z z π < τ < π ε π 4 π < τ < π ε π 4 直交する直線左回り円右回り円 9/
10 z τ θ τ θ + π ' ' z < ε < π 4 π 4 < ε < 左回りだ円 直交する右回りだ円 図.9 ジョーンズベクトルによるいくつかの状態 注意点として, ジョーンズベクトル表現には波の伝搬方向が含まれていないことがある. 通常は右手座標系を仮定しているので普通のベクトル表現と同じであるが, 波の後側から見る場合には座標軸の方向に注意が必要である. 比 ρ によるジョーンズベクトル表現 ベクトル成分の数式表現として一般に直角座標成分が用いられる. しかし, 直線基底 ( 直角座標系 ) だけでなく, 円, だ円などの直交基底 ( 座標系 ) もある. 直角座標成分だけでなく, 他の座標成分で表現しなければならない場合もでてくるので, ここでは座標系を考慮した比によるベクトル表現を考えよう. 基底に対応して表現方法も変わるので, まず任意の基底 ( 座標系 ) で表すことを考える. 互いに直交する単位ベクトル a, bをもつ基底 ABに対して, その電界ベクトルは次のように書くことができる. E ( AB ) E A a + E B b (.7) ここで,E A と E B はベクトルの成分で, 一般には複素数である.(AB) は基底を明示するために付けている. これを使って比は次のように定義される. ρ AB E B E A E B E A e (φ B - φ A) ρ AB e δ AB (.8) δ AB φ B - φ A は E A と E B の位相差である. この比 ρ AB によって電界をジョーンズベクトル表現すると E ( AB ) E A E B E A e φ A ρ AB E A e φ A + E B E B E A E A + E B E B E A E A ρ AB E e φ A + ρ AB ρ AB ρ AB (.9) ただし, E E A E A + E B E B (.3) /
11 比を使ったこの表現方法も状態のつの表し方であり, コヒーレント波の解析でよく用いられる. 任意の基底変換とベクトル変換については付録.3に述べることとし, ここでは最もよく使われる直線基底 (HV) の比 ρ HV によるジョーンズベクトルを考察しておく. 直線基底 (HV) で電界ベクトルは E ( HV ) H + E V V (.3) であるので, 比 ρ HV は ρ HV E V E V e (φ V - φ H ) tan γ HV e δ HV (.3) ここで γ HV は図. に定義される角度である. (V) + E V cos γ HV E V + E V sin γ HV (.33) E 例えば振幅が の水平の場合,E V となるので ρ HV となり γ HV (H) E ( HV ) H + V + (.34a) 図.. 電界成分と角度 45 傾いた直線は ρ HV E ( HV ) + (.34b) である. また, 左回り円 L を表現しようとする場合,IEEE の定義では, E V, δ HV φ V - φ H π, ρ HV なので L ( HV ) LHC + ( ) ( ) (.34c) 同様に右回り円では,ρ HV になるので R ( HV ) + ( - ) (.34d) となる. しかし, 本文では基底変換の性質も含めて, 右回り円 (RHC) に対しては以下の表現を使う. R ( HV ) RHC (.34e) なお,IEEEの定義[6] では,(.34c),(.34d) のジョーンズベクトル表現で円が表現されており, 互いに複素共役の関係にある. そこまでは正しいが, それを使った基底変換ではユニタリ行列の行列式が +にならないのでLR 間の位相保持ができない. そのため位相を扱うレーダポーラリメトリでは大きな問題が生じてくる. /
12 物理的には同じ状態を表していても, 基底が異なると比は異なった値となり, ベクトルも変化する. 表.にいくつかの状態を示す. 表. 幾何学的パラメータ (ε, τ ), 比と Jones ベクトルによる代表的な状態の表現 Polarization Geometric HV basis LR basis Linear Horizontal (H) Linear Vertical (V) 45 deg. Linear 35 deg. Linear Left Handed Circular Right Handed Circular ε τ ρ HV E ρ LR E π π 4 π 4 π 4 π 4 - an an - ところで, 比 ρ となって発散してしまう場合には, 解析に不便なことがある. そのような場合, 以下のようにスピナーパラメータを使うことがある.(.) を変形すると瞬時ベクトルは次のようになる. ε ( z, t ) + Re cos γ sin γ e δ e ω t kz + α (.38) この [ ] で囲まれた項目はスピナーと呼ばれる. スピナーのパラメータ γ, δ は, ポアンカレ球上で状態 を指定するときにも使われる. また, 後述するようにベクトルとして p cos τ sin τ sin τ cos τ cos ε sin ε (.39) を直接使うこともある. これは式 (.) を用いることと同等であり, 幾何学的パラメータによってジョーンズベクトルを明示することが可能である. E ( HV ) A cos τ cos ε sinτ sin ε sinτ cos ε + cos τ sin ε (.4) /
13 .4 ストークスベクトルによる表現風に揺れている麦畑をレーダで観測している場合を想定してみる. レーダパルスの照射時間が長い場合 ( 例えば数ミリ秒の範囲 ), 麦は揺らいでいると考えられる. 反射波は, 麦畑中の数多くの散乱点からの反射波の合計となり, その合計位相は計測時間中でもランダムに変動する. 一方, 照射時間が短い場合 ( 例えば数ナノ秒の範囲 ), 麦畑は静止していると考えられ, 計測時間内で反射波の位相は一定と見なせる. 揺らぎの程度は計測時間とターゲットの揺らぐ速度の相対関係に依存する. 一般に計測時間が十分短ければターゲットは静止していると見なせるので, 反射波は位相のそろったコヒーレント波になり, 逆に計測時間が長い場合には揺らぎのために位相が不揃いなインコヒーレント波に近づく. したがって, レーダ反射波は位相の揃ったコヒーレント波と位相の揃っていないインコヒーレント波から成り立っていると考えることができる ( 図.を参照 ). コヒーレント波をCompletel polarized wave ( 完全 ) ともいう. 一方, インコヒーレント波を Completel unpolarized wave ( 完全無 ) ともいう. 両者が混ざり合っている波を部分 (Partiall polarized wave) という. 送信にはコヒーレント波を送るが, 揺らぎによってインコヒーレント波になることをde-polarizationという. 一方, 完全にした波がターゲットに当たって状態を変えた場合もdepolarizationという言葉を使うことがある. 例えば,H で送信してV が発生した場合,depolarizationと言われることがある. しかし, この場合,V が位相が揃っていれば ( コヒーレントであれば ) 波全体として完全のままである. 波の性質から考えて, 交差が発生する場合には "re-polarization" という言葉を使った方が適切と思われる [5]. この点も研究者によって統一されていない状況にある. Coherent wave scattered wave コヒーレント波 ( 位相が揃っている ) 完全 Completel Polarized wave 完全 repolarization depolarization ( 位相が不揃い ) インコヒーレント波 部分 Partiall Polarized wave していない波 Unpolarized wave 図. 散乱波位相の揃い具合と度合い 前項まで完全 (Completel polarized wave) について扱ってきた. 完全した波とは E A, E B, δ AB が観測時間中に定数であるか, あるいは少なくとも時間に関して非常にゆっくり変動する波で, 位相がそろっているコヒーレントな波と等価である. しかし, 観測時間中に位相がランダムに変わる波や部分的にした波を扱うのには今までの手法で取り扱うことはできない. 完全も含め, これらのすべての波を取り扱うにはストークスパラメータを用いなければならない. ストークスパラメータは85 年に Sir George Stokes によってつくられたものである. ストークスパラメータの利点は全ての要素が実数であり, 電力測定によって決定できることである. 特に光 ミリ波のような高い周波数領域では正確な位相測定が困難なため, 波の情報を得る際に威力を発揮する. 3/
14 (a) 完全に対するストークスベクトル ストークスベクトルは g で表され, その4 成分 g, g, g, g 3 一周波数の完全した平面波では次の関係がある. がストークスパラメータと呼ばれている. 単 g g g g g 3 + EV EV Re E V Im E V + EV EV E V cos δ E V sin δ A cos τ cos ε sin τ cos ε sin ε (.4), E V は, E V 成分の振幅,δ は相対位相である. 完全に対しては次の関係が成り立つ. g g + g + g 3 (.4) これらの成分は図.5に示したポアンカレ球の直角座標成分に対応している. また, これらの物理的な内容は以下のベクトル変換から了解される. 円と直線のベクトル成分の関係は付録.3 より これから次式が得られる. E L E V, E R + E V (.4) E L E L E L + E V + Im E V E R E R E R + E V Im E V E L E R E V + Re E V (.43) ストークスパラメータを円成分で表すと次のようになる. g + E V E L + E R g E V Im E L E R g Re E V g 3 Im E V Re E L E R E L E R (.44) 45, 35 回転した直線基底では E 45 + E V E 35 + E V (.45) なので, E 45 E 45 E 45 + E V + Re E V 4/
15 E 35 E 35 E 35 + E V Re E V E 45 E 35 + E V Im E V (.46) が得られ, ストークスパラメータに変換すると次式が得られる. g + E V E 45 + E 35 g E H E V Re E 45 E 35 g Re E V g 3 Im E V E 45 - E 35 Im E 45 E 35 (.47) したがって (.44) と (.47) を使ってストークスパラメータは表.のように表現することが可能である. この表より,g は全電力を表し基底に依存しない量であることが分かる.g は水平と垂直の電力差,g は45 と35 の直線電力差,g 3 は左回り円と右回り円の電力差を表わしていることが分かる. もし,g, g, g 3 のいずれかがでなければ, 完全した成分が存在することになる. 表. ストークスパラメータの表現 Stokes Parameter HV 45/35 Linear LR Geometric Parameter g + E V E 45 + E 35 E L + E R A g E V Re E 45 E 35 Im E L E R A cos ε cos τ g Re E V E 45 E 35 Re E L E R A cos ε sin τ g 3 Im E V Im E 45 E 35 E L E R A sin ε 一方, ストークスパラメータは幾何学的パラメータとも直結しており, ストークスパラメータを測定することによって状態を求めることができる. A g (.48) sin ε g 3 g tan τ g g (.49) (.5) 5/
16 (b) 部分に対するストークスベクトル インコヒーレント波 ( 位相の揃っていない波 ) や部分的にインコヒーレントな波を扱う際に集合平均が使われる. エルゴード性を仮定して時間平均あるいは空間集合平均をとってみる. 次のストークスベクトル表現では平均操作を示す. g g g g + E V E V Re E V g 3 Im E V (.59) これから g g + g + g 3 (.6) が成り立つことが分かる. 全電力の中にどの程度コヒーレントな成分が含まれているかを表す指標として度 (DoP:Degree of Polarization) が定義されている. Degree of Polarization DoP g + g + g 3 g (.6) Degree of Polarization による波の分類 DoP は完全 (completel polarized wave) といい, 完全にコヒーレントな波を表す. ストークスパラメータの間には次の関係式が成り立つ. g g + g + g 3 (.63) DoP を完全無 (completel unpolarized wave) といい, 完全にインコヒーレントな波となる. ストー クスパラメータは次のようになる. g g g g 3 (.64) DoP を部分という. 測定されるほとんどの波がこの範疇に入る. 部分した波はコヒーレント 波とインコヒーレント波の和であるので次のようにも書くことができる. g + g + g 3 q (.65) g g g g g 3 q g g g 3 + g - q polarized + unpolarized (.66) 6/
17 .5 パラメータとポアンカレ球 視覚的な表現方法としてポアンカレ球がある. 図.3にポアンカレ球を示す. 数学者ポアンカレ (Poincare) によって考案されたものである. 球面上の一点は, ある一つの状態を示しており, すべての状態と 対 の対応がある. 球面上の点によって状態が指定できる. LHC V H RHC 図.3 ポアンカレ球と状態 ( 上半球は左回り, 下半球は右回り ) 球面上の座標を指定するにはいくつかの方法がある. 今まで示したパラメータに角度 γ HV と δ HV, あるいは幾何学的パラメータ ε, τ がある. それらのパラメータの取り方を図.4に示す. なぜこのような出発点 Hとパラメータの取り方をするかは, 各パラメータ間の関係やストークスベクトルによる表現とも密接に関わっており, 結果的に非常にうまくできている. γ γ HV は, 赤道上の点 H( 水平を表す ) から球面上の点 Pまでの大圏行路距離 HPを表し, γ π の範囲で球の裏側までカバーする. また δ δ HV φ φ は, 点 Hにおいて赤道とHPのなす角度 ( π δ π ) である. 例えば,δ φ φ π / は左回り円 (LHC) であり,δ π / は右回り円 (RHC) になっている. 一方, 幾何学的パラメータ ( ε, τ ) については図.4 に示すように τ が OH 軸から測られる赤道上の角度 で, 経度 ( π τ π ) に対応する.+Y 軸に相当する角度は τ 9 なので,τ 45 の直線を表す. そ して点 H の裏側は τ 9 となり, この角度は垂直になっている. また,ε は赤道面と OP 軸のなす角度 で, 緯度 ( π/ ε π/ ) に対応している. 北極は ε 9 (ε 45 ) で LHC を表し, 南極は ε 9 (ε 45 ) で RHC を表す ( 図.6). したがって, 各パラメータの定義式と一致している. 7/
18 Z P γ H δ τ ε Y X 図.4 ポアンカレ球と幾何学的パラメータ スピナーパラメータ γ HV γ, δ HV δ は, 幾何学的パラメータ ε, τ と次の関係がある. 図.5 より sin ε sin γ sin δ (.67) 式 (.8) を使って tan τ tan γ cos δ tan γ cos δ (.68) tan γ また, 逆の関係として sin γ cos τ を両辺に掛けて整理すると tan δ sin ε sin γ + tan τ tan γ (.69) cos γ cos τ cos ε (.7) sin ε tan τ cos γ tan ε sin τ (.7) 式 (.67) から (.7) までの関係を図で書くと, 結果的に図.5 のようになっている. 最も特徴的なことは, ストークスベクトル成分 ( g, g, g 3 ) がポアンカレー球の直角座標軸成分になっていることである. 通常の球座標でX 軸が g,y 軸が g,z 軸が g 3 に対応する. また, 幾何学的パラメータ ( ε, τ ) は, 図.4のように緯度, 経度を表わしており,τ が球座標における ϕ 方向, π ε が θ 方向に相当する. 緯度 ε 経度 τ 式 (.4) から g g cos τ cos ε cos γ (.7) 8/
19 なので,cos γ はStokesベクトルgがX 軸となす角の方向余弦である. それゆえ, 点 Hから点 Pまでのアーク距離 ( 大圏行路距離 ) は,g とすれば, HP g (γ HV ) γ のように表せる. また, 角度 δ は赤道面と最大円 ( アーク距離方向 ) とのなす角度であり,XOY 面とXOP 面のなす角度に等しい. 点 PをYOZ 面に投影すれば,Y 軸と投影点 P から作られる角度 YOP' δ となる.YOZ 面で次式が成り立つことが分かる. tan δ tan YOP' g 3 g (.73) したがって, ポアンカレ球上の点 P は, 同じ場所でも状態の表現方法 ( γ, δ ), γ π, π δ π ( τ, ε ), π τ π, π 4 ε π 4 ( g, g, g 3 ), ( g, g, g 3 ) によって図.5 のように表されることが分かる. このうち, 最も分かり易いパラメータは ( τ, ε ) と ( g, g, g 3 ) であろう.( τ, ε ) は全体の表記の基本をなしている. Z g 3 P P' γ g g 3 X H g δ ε τ δ g g + g + g 3 g Y g O Q P τ, ε g τ+ π, ε 図.5 ポアンカレ球とストークスベクトル図.6 直交状態 (P と Q) 重要な点として, 図.6のようにポアンカレ球上にある点 Pを指定すると, 球の真裏の点 Q (anti-podal point) は直交した状態になっていることである. 例えば,Hの裏側はVであり,HとVは互いに直交している. また, 北極は左回り円 (LHC), 南極は右回り円 (RHC) で直交する. この直交性は球面上のどの点でも成り立っている. 9/
20 .6 ベクトルによる表現 ポアンカレ球の中心を貫く直線によって直交する状態が直観的にも理解できるので, 改めて式の上でも直交する状態を考えてみよう. 再度, 式 (.) をふり返ってみる. e φ e φ A cos τ sin τ sin τ cos τ cos ε sin ε e φ ξ (.) この式から位相 φ ξ を無視して ( 正確に測定することが難しいため ), ベクトル p を p p ( τ, ε ) cos τ sin τ sin τ cos τ cos ε sin ε (.74) とおく. これに直交する状態は, ポアンカレ球の裏側に配置しているので, τ τ + π (τ τ + π ) ε ε ( ε ε ) (.75) とすれば得られることになる. したがって, 直交するベクトル p は次式で与えられる ( 図.7). p p ( τ + π, ε ) sin τ cos τ cos τ sin τ cos ε sin ε (.76) τ + π τ 図.7 直交状態 例えば, 代表的な状態は式 (.74),(.76) のベクトルを使って以下のように表される. 水平 τ, ε p p (, ) (.77a) 直交 ( 垂直 ) p p ( π, ) (.77b) 左回り円 ε π 4 p p ( τ, π 4 ) cos τ sin τ sin τ cos τ e τ (.78) 直交円 ( 右回り ) p p ( τ + π, π 4 sin τ cos τ ) cos τ sin τ e τ (.79) /
21 これらの結果は表. のものと同じ表現であり, ジョーンズベクトルとも等価である. 円において e τ, e τ の項目は傾き角の回転を表し, 円を回転しても同じ円になるので意味をもたな い. もし,τ ととれば, 左回りと右回りのベクトルとして L R (.8) が得られる ( 注.4). ベクトルは次の直交 ( ユニタリ内積 ) 条件を満たしている. p p (.8).3 パラメータ間の関係 今まで, 電界の振幅, 位相から出発し, 各種パラメータによってだ円を表現してきた. 表現方法はいろいろあるが, 本質的に同じものを指している. 視覚的に状態を捉えるには, ポアンカレ球が最も優れている. これらのパラメータの相互関係を図.3.に示す. δ A + sin ε sin δ + tan τ cos δ g + g A + tan γ g cos δ g 3 sin δ A, ε, τ A, γ, δ tan τ tan γ cos δ sin ε sin γ sin δ g A g A cos τ cos ε g A sin τ cos ε g 3 A sin ε cos γ g g tan δ g 3 g g, g, g, g 3 図.3. だ円を表すパラメータの相互関係 /
22 なお, 比と幾何学的パラメータには次の関係が成り立つ. 電界表現 E V A cos τ sin τ sin τ cos τ cos ε sin ε (.3.) 比は ellipticit, tilt angle を使って表現できる. ρ E V したがって次の関係が導かれる. tan τ Re ρ ρ sinτ cosε + cosτ sinε cosτ cosε sinτ sinε tan τ + tan ε tan τ tan ε (.3.), sin ε Im ρ + ρ (.3.3) この関係は図.3. のように表すことができる. ρ E V ρ r + ρ i tanτ Re ρ ρ sin ε Im ρ + ρ ρ tan τ + tan ε tan τ tan ε τ, ε 図.3. 比と幾何学的パラメータの関係 /
平面波
 平面波 図.に示すように, 波源 ( 送信アンテナあるいは散乱点 ) から遠い位置で, 観測点 Pにおける波の状態を考えてみる. 遠いとは, 波長 λ に比べて距離 が十分大きいことを意味しており, 観測点 Pの近くでは, 等位相面が平面とみなせる状態にある. 平面波とは波の等位相面が平面になっている波のことである. 通信や計測を行うとき, 遠方における波の振舞いは平面波で近似できる. したがって平面波の性質を理解することが最も重要である.
平面波 図.に示すように, 波源 ( 送信アンテナあるいは散乱点 ) から遠い位置で, 観測点 Pにおける波の状態を考えてみる. 遠いとは, 波長 λ に比べて距離 が十分大きいことを意味しており, 観測点 Pの近くでは, 等位相面が平面とみなせる状態にある. 平面波とは波の等位相面が平面になっている波のことである. 通信や計測を行うとき, 遠方における波の振舞いは平面波で近似できる. したがって平面波の性質を理解することが最も重要である.
PowerPoint Presentation
 付録 2 2 次元アフィン変換 直交変換 たたみ込み 1.2 次元のアフィン変換 座標 (x,y ) を (x,y) に移すことを 2 次元での変換. 特に, 変換が と書けるとき, アフィン変換, アフィン変換は, その 1 次の項による変換 と 0 次の項による変換 アフィン変換 0 次の項は平行移動 1 次の項は座標 (x, y ) をベクトルと考えて とすれば このようなもの 2 次元ベクトルの線形写像
付録 2 2 次元アフィン変換 直交変換 たたみ込み 1.2 次元のアフィン変換 座標 (x,y ) を (x,y) に移すことを 2 次元での変換. 特に, 変換が と書けるとき, アフィン変換, アフィン変換は, その 1 次の項による変換 と 0 次の項による変換 アフィン変換 0 次の項は平行移動 1 次の項は座標 (x, y ) をベクトルと考えて とすれば このようなもの 2 次元ベクトルの線形写像
座標系.rtf
 2 章座標系 場 空間は3 次元なので, ベクトルを表現するには少なくとも3 成分を指定する必要がある. そのために座標系が必要となる. 座標系として最も一般的なものは,,, 成分を使った直角座標系である. しかし, 他にも円柱座標, 球座標, だ円座標, 放物線座標など様々なものがある. 現在までに3 成分で変数分離可能な座標系は11 個あるといわれている (Moon & Spencer, Field
2 章座標系 場 空間は3 次元なので, ベクトルを表現するには少なくとも3 成分を指定する必要がある. そのために座標系が必要となる. 座標系として最も一般的なものは,,, 成分を使った直角座標系である. しかし, 他にも円柱座標, 球座標, だ円座標, 放物線座標など様々なものがある. 現在までに3 成分で変数分離可能な座標系は11 個あるといわれている (Moon & Spencer, Field
反射係数
 平面波の反射と透過 電磁波の性質として, 反射と透過は最も基礎的な現象である. 我々の生活している空間は, 各種の形状を持った媒質で構成されている. 人間から見れば, 空気, 水, 木, 土, 火, 金属, プラスチックなど, 全く異なるものに見えるが, 電磁波からすると誘電率, 透磁率, 導電率が異なるだけである. 磁性体を除く媒質は比透磁率がで, ほとんど媒質に当てはまるので, 実質的に我々の身の回りの媒質で,
平面波の反射と透過 電磁波の性質として, 反射と透過は最も基礎的な現象である. 我々の生活している空間は, 各種の形状を持った媒質で構成されている. 人間から見れば, 空気, 水, 木, 土, 火, 金属, プラスチックなど, 全く異なるものに見えるが, 電磁波からすると誘電率, 透磁率, 導電率が異なるだけである. 磁性体を除く媒質は比透磁率がで, ほとんど媒質に当てはまるので, 実質的に我々の身の回りの媒質で,
vecrot
 1. ベクトル ベクトル : 方向を持つ量 ベクトルには 1 方向 2 大きさ ( 長さ ) という 2 つの属性がある ベクトルの例 : 物体の移動速度 移動量電場 磁場の強さ風速力トルクなど 2. ベクトルの表現 2.1 矢印で表現される 矢印の長さ : ベクトルの大きさ 矢印の向き : ベクトルの方向 2.2 2 個の点を用いて表現する 始点 () と終点 () を結ぶ半直線の向き : ベクトルの方向
1. ベクトル ベクトル : 方向を持つ量 ベクトルには 1 方向 2 大きさ ( 長さ ) という 2 つの属性がある ベクトルの例 : 物体の移動速度 移動量電場 磁場の強さ風速力トルクなど 2. ベクトルの表現 2.1 矢印で表現される 矢印の長さ : ベクトルの大きさ 矢印の向き : ベクトルの方向 2.2 2 個の点を用いて表現する 始点 () と終点 () を結ぶ半直線の向き : ベクトルの方向
2011年度 筑波大・理系数学
 0 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ O を原点とするy 平面において, 直線 y= の を満たす部分をC とする () C 上に点 A( t, ) をとるとき, 線分 OA の垂直二等分線の方程式を求めよ () 点 A が C 全体を動くとき, 線分 OA の垂直二等分線が通過する範囲を求め, それ を図示せよ -- 0 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ
0 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ O を原点とするy 平面において, 直線 y= の を満たす部分をC とする () C 上に点 A( t, ) をとるとき, 線分 OA の垂直二等分線の方程式を求めよ () 点 A が C 全体を動くとき, 線分 OA の垂直二等分線が通過する範囲を求め, それ を図示せよ -- 0 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ
パソコンシミュレータの現状
 第 2 章微分 偏微分, 写像 豊橋技術科学大学森謙一郎 2. 連続関数と微分 工学において物理現象を支配する方程式は微分方程式で表されていることが多く, 有限要素法も微分方程式を解く数値解析法であり, 定式化においては微分 積分が一般的に用いられており. 数学の基礎知識が必要になる. 図 2. に示すように, 微分は連続な関数 f() の傾きを求めることであり, 微小な に対して傾きを表し, を無限に
第 2 章微分 偏微分, 写像 豊橋技術科学大学森謙一郎 2. 連続関数と微分 工学において物理現象を支配する方程式は微分方程式で表されていることが多く, 有限要素法も微分方程式を解く数値解析法であり, 定式化においては微分 積分が一般的に用いられており. 数学の基礎知識が必要になる. 図 2. に示すように, 微分は連続な関数 f() の傾きを求めることであり, 微小な に対して傾きを表し, を無限に
例 e 指数関数的に減衰する信号を h( a < + a a すると, それらのラプラス変換は, H ( ) { e } e インパルス応答が h( a < ( ただし a >, U( ) { } となるシステムにステップ信号 ( y( のラプラス変換 Y () は, Y ( ) H ( ) X (
 第 週ラプラス変換 教科書 p.34~ 目標ラプラス変換の定義と意味を理解する フーリエ変換や Z 変換と並ぶ 信号解析やシステム設計における重要なツール ラプラス変換は波動現象や電気回路など様々な分野で 微分方程式を解くために利用されてきた ラプラス変換を用いることで微分方程式は代数方程式に変換される また 工学上使われる主要な関数のラプラス変換は簡単な形の関数で表されるので これを ラプラス変換表
第 週ラプラス変換 教科書 p.34~ 目標ラプラス変換の定義と意味を理解する フーリエ変換や Z 変換と並ぶ 信号解析やシステム設計における重要なツール ラプラス変換は波動現象や電気回路など様々な分野で 微分方程式を解くために利用されてきた ラプラス変換を用いることで微分方程式は代数方程式に変換される また 工学上使われる主要な関数のラプラス変換は簡単な形の関数で表されるので これを ラプラス変換表
ベクトルの基礎.rtf
 章ベクトルの表現方法 ベクトルは大きさと方向を持つ量である. 図.に示すように始点 Pから終点 Qに向かう有向線分として で表現する. 大きさは矢印の長さに対応している. Q P 図. ベクトルの表現方法 文字を使ったベクトルの表記方法として, あるいは の表記が用いられるが, このテキストでは太字表示 を採用する. 専門書では太字で書く の表記が一般的であり, 矢印を付ける表記は用いない. なお,
章ベクトルの表現方法 ベクトルは大きさと方向を持つ量である. 図.に示すように始点 Pから終点 Qに向かう有向線分として で表現する. 大きさは矢印の長さに対応している. Q P 図. ベクトルの表現方法 文字を使ったベクトルの表記方法として, あるいは の表記が用いられるが, このテキストでは太字表示 を採用する. 専門書では太字で書く の表記が一般的であり, 矢印を付ける表記は用いない. なお,
ベクトル公式.rtf
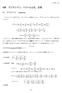 6 章ラプラシアン, ベクトル公式, 定理 6.1 ラプラシアン Laplacian φ はベクトル量である. そこでさらに発散をとると, φ はどういう形になるであろうか? φ = a + a + a φ a + a φ + a φ = φ + φ + φ = 2 φ + 2 φ 2 + 2 φ 2 2 φ = 2 φ 2 + 2 φ 2 + 2 φ 2 = 2 φ したがって,2 階の偏微分演算となる.
6 章ラプラシアン, ベクトル公式, 定理 6.1 ラプラシアン Laplacian φ はベクトル量である. そこでさらに発散をとると, φ はどういう形になるであろうか? φ = a + a + a φ a + a φ + a φ = φ + φ + φ = 2 φ + 2 φ 2 + 2 φ 2 2 φ = 2 φ 2 + 2 φ 2 + 2 φ 2 = 2 φ したがって,2 階の偏微分演算となる.
スライド タイトルなし
 線形代数 演習 (008 年度版 ) 008/5/6 線形代数 演習 Ⅰ コンピュータ グラフィックス, 次曲面と線形代数指南書第七の巻 直交行列, 実対称行列とその対角化, 次曲線池田勉龍谷大学理工学部数理情報学科 実行列, 正方行列, 実対称行列, 直交行列 a a N A am a MN 実行列 : すべての成分 a が実数である行列 ij ji ij 正方行列 : 行の数と列の数が等しい (
線形代数 演習 (008 年度版 ) 008/5/6 線形代数 演習 Ⅰ コンピュータ グラフィックス, 次曲面と線形代数指南書第七の巻 直交行列, 実対称行列とその対角化, 次曲線池田勉龍谷大学理工学部数理情報学科 実行列, 正方行列, 実対称行列, 直交行列 a a N A am a MN 実行列 : すべての成分 a が実数である行列 ij ji ij 正方行列 : 行の数と列の数が等しい (
第 4 週コンボリューションその 2, 正弦波による分解 教科書 p. 16~ 目標コンボリューションの演習. 正弦波による信号の分解の考え方の理解. 正弦波の複素表現を学ぶ. 演習問題 問 1. 以下の図にならって,1 と 2 の δ 関数を図示せよ δ (t) 2
 第 4 週コンボリューションその, 正弦波による分解 教科書 p. 6~ 目標コンボリューションの演習. 正弦波による信号の分解の考え方の理解. 正弦波の複素表現を学ぶ. 演習問題 問. 以下の図にならって, と の δ 関数を図示せよ. - - - δ () δ ( ) - - - 図 δ 関数の図示の例 δ ( ) δ ( ) δ ( ) δ ( ) δ ( ) - - - - - - - -
第 4 週コンボリューションその, 正弦波による分解 教科書 p. 6~ 目標コンボリューションの演習. 正弦波による信号の分解の考え方の理解. 正弦波の複素表現を学ぶ. 演習問題 問. 以下の図にならって, と の δ 関数を図示せよ. - - - δ () δ ( ) - - - 図 δ 関数の図示の例 δ ( ) δ ( ) δ ( ) δ ( ) δ ( ) - - - - - - - -
<4D F736F F D20824F F6490CF95AA82C696CA90CF95AA2E646F63>
 1/15 平成 3 年 3 月 4 日午後 6 時 49 分 5 ベクトルの 重積分と面積分 5 重積分と面積分 Ⅰ. 重積分 と で 回積分することを 重積分 といいます この 重積分は何を意味しているのでしょう? 通常の積分 (1 重積分 ) では C d 図 1a 1 f d (5.1) 1 f d f ( ) は 図形的には図 1a のように面積を表しています つまり 1 f ( ) を高さとしてプロットすると図
1/15 平成 3 年 3 月 4 日午後 6 時 49 分 5 ベクトルの 重積分と面積分 5 重積分と面積分 Ⅰ. 重積分 と で 回積分することを 重積分 といいます この 重積分は何を意味しているのでしょう? 通常の積分 (1 重積分 ) では C d 図 1a 1 f d (5.1) 1 f d f ( ) は 図形的には図 1a のように面積を表しています つまり 1 f ( ) を高さとしてプロットすると図
Microsoft PowerPoint - 10.pptx
 m u. 固有値とその応用 8/7/( 水 ). 固有値とその応用 固有値と固有ベクトル 行列による写像から固有ベクトルへ m m 行列 によって線形写像 f : R R が表せることを見てきた ここでは 次元平面の行列による写像を調べる とし 写像 f : を考える R R まず 単位ベクトルの像 u y y f : R R u u, u この事から 線形写像の性質を用いると 次の格子上の点全ての写像先が求まる
m u. 固有値とその応用 8/7/( 水 ). 固有値とその応用 固有値と固有ベクトル 行列による写像から固有ベクトルへ m m 行列 によって線形写像 f : R R が表せることを見てきた ここでは 次元平面の行列による写像を調べる とし 写像 f : を考える R R まず 単位ベクトルの像 u y y f : R R u u, u この事から 線形写像の性質を用いると 次の格子上の点全ての写像先が求まる
補足 中学で学習したフレミング左手の法則 ( 電 磁 力 ) と関連付けると覚えやすい 電磁力は電流と磁界の外積で表される 力 F 磁 電磁力 F li 右ねじの回転の向き電 li ( l は導線の長さ ) 補足 有向線分とベクトル有向線分 : 矢印の位
 http://totemt.sur.ne.p 外積 ( ベクトル積 ) の活用 ( 面積, 法線ベクトル, 平面の方程式 ) 3 次元空間の つのベクトルの積が つのベクトルを与えるようなベクトルの掛け算 ベクトルの積がベクトルを与えることからベクトル積とも呼ばれる これに対し内積は符号と大きさをもつ量 ( スカラー量 ) を与えるので, スカラー積とも呼ばれる 外積を使うと, 平行四辺形や三角形の面積,
http://totemt.sur.ne.p 外積 ( ベクトル積 ) の活用 ( 面積, 法線ベクトル, 平面の方程式 ) 3 次元空間の つのベクトルの積が つのベクトルを与えるようなベクトルの掛け算 ベクトルの積がベクトルを与えることからベクトル積とも呼ばれる これに対し内積は符号と大きさをもつ量 ( スカラー量 ) を与えるので, スカラー積とも呼ばれる 外積を使うと, 平行四辺形や三角形の面積,
Microsoft PowerPoint - H21生物計算化学2.ppt
 演算子の行列表現 > L いま 次元ベクトル空間の基底をケットと書くことにする この基底は完全系を成すとすると 空間内の任意のケットベクトルは > > > これより 一度基底を与えてしまえば 任意のベクトルはその基底についての成分で完全に記述することができる これらの成分を列行列の形に書くと M これをベクトル の基底 { >} による行列表現という ところで 行列 A の共役 dont 行列は A
演算子の行列表現 > L いま 次元ベクトル空間の基底をケットと書くことにする この基底は完全系を成すとすると 空間内の任意のケットベクトルは > > > これより 一度基底を与えてしまえば 任意のベクトルはその基底についての成分で完全に記述することができる これらの成分を列行列の形に書くと M これをベクトル の基底 { >} による行列表現という ところで 行列 A の共役 dont 行列は A
<4D F736F F D E682568FCD CC82B982F192668BAD9378>
 7. 組み合わせ応力 7.7. 応力の座標変換載荷 ( 要素 の上方右側にずれている位置での載荷を想定 図 ( この場合正 ( この場合負 応力の座標変換の知識は なぜ必要か? 例 土の二つの基本的せん断変形モード : - 三軸圧縮変形 - 単純せん断変形 一面せん断変形両者でのせん断強度の関連を理解するためには 応力の座標変換を理解する必要がある 例 粘着力のない土 ( 代表例 乾燥した砂 のせん断破壊は
7. 組み合わせ応力 7.7. 応力の座標変換載荷 ( 要素 の上方右側にずれている位置での載荷を想定 図 ( この場合正 ( この場合負 応力の座標変換の知識は なぜ必要か? 例 土の二つの基本的せん断変形モード : - 三軸圧縮変形 - 単純せん断変形 一面せん断変形両者でのせん断強度の関連を理解するためには 応力の座標変換を理解する必要がある 例 粘着力のない土 ( 代表例 乾燥した砂 のせん断破壊は
DVIOUT
 第 章 離散フーリエ変換 離散フーリエ変換 これまで 私たちは連続関数に対するフーリエ変換およびフーリエ積分 ( 逆フーリエ変換 ) について学んできました この節では フーリエ変換を離散化した離散フーリエ変換について学びましょう 自然現象 ( 音声 ) などを観測して得られる波 ( 信号値 ; 観測値 ) は 通常 電気信号による連続的な波として観測機器から出力されます しかしながら コンピュータはこの様な連続的な波を直接扱うことができないため
第 章 離散フーリエ変換 離散フーリエ変換 これまで 私たちは連続関数に対するフーリエ変換およびフーリエ積分 ( 逆フーリエ変換 ) について学んできました この節では フーリエ変換を離散化した離散フーリエ変換について学びましょう 自然現象 ( 音声 ) などを観測して得られる波 ( 信号値 ; 観測値 ) は 通常 電気信号による連続的な波として観測機器から出力されます しかしながら コンピュータはこの様な連続的な波を直接扱うことができないため
Microsoft Word - thesis.doc
 剛体の基礎理論 -. 剛体の基礎理論初めに本論文で大域的に使用する記号を定義する. 使用する記号トルク撃力力角運動量角速度姿勢対角化された慣性テンソル慣性テンソル運動量速度位置質量時間 J W f F P p .. 質点の並進運動 質点は位置 と速度 P を用いる. ニュートンの運動方程式 という状態を持つ. 但し ここでは速度ではなく運動量 F P F.... より質点の運動は既に明らかであり 質点の状態ベクトル
剛体の基礎理論 -. 剛体の基礎理論初めに本論文で大域的に使用する記号を定義する. 使用する記号トルク撃力力角運動量角速度姿勢対角化された慣性テンソル慣性テンソル運動量速度位置質量時間 J W f F P p .. 質点の並進運動 質点は位置 と速度 P を用いる. ニュートンの運動方程式 という状態を持つ. 但し ここでは速度ではなく運動量 F P F.... より質点の運動は既に明らかであり 質点の状態ベクトル
Microsoft Word - Chap11
 第 章 次元回転群とそのリー代数. SO のリー代数. 節でリー代数を定義したが 以下にその定義を再録する なお 多くの教科書に従って本章以降は ep t A の代わりに ep t と書くこととする 定義.. G を 次の線型リー群とすると 任意の実数 t に対して ep t G となる gl C の全体をGのリー代数 またはリー環 という 例えば ep t が 次の特殊直交群 SO の元であれば
第 章 次元回転群とそのリー代数. SO のリー代数. 節でリー代数を定義したが 以下にその定義を再録する なお 多くの教科書に従って本章以降は ep t A の代わりに ep t と書くこととする 定義.. G を 次の線型リー群とすると 任意の実数 t に対して ep t G となる gl C の全体をGのリー代数 またはリー環 という 例えば ep t が 次の特殊直交群 SO の元であれば
OCW-iダランベールの原理
 講義名連続体力学配布資料 OCW- 第 2 回ダランベールの原理 無機材料工学科准教授安田公一 1 はじめに今回の講義では, まず, 前半でダランベールの原理について説明する これを用いると, 動力学の問題を静力学の問題として解くことができ, さらに, 前回の仮想仕事の原理を適用すると動力学問題も簡単に解くことができるようになる また, 後半では, ダランベールの原理の応用として ラグランジュ方程式の導出を示す
講義名連続体力学配布資料 OCW- 第 2 回ダランベールの原理 無機材料工学科准教授安田公一 1 はじめに今回の講義では, まず, 前半でダランベールの原理について説明する これを用いると, 動力学の問題を静力学の問題として解くことができ, さらに, 前回の仮想仕事の原理を適用すると動力学問題も簡単に解くことができるようになる また, 後半では, ダランベールの原理の応用として ラグランジュ方程式の導出を示す
Microsoft PowerPoint - 第3回2.ppt
 講義内容 講義内容 次元ベクトル 関数の直交性フーリエ級数 次元代表的な対の諸性質コンボリューション たたみこみ積分 サンプリング定理 次元離散 次元空間周波数の概念 次元代表的な 次元対 次元離散 次元ベクトル 関数の直交性フーリエ級数 次元代表的な対の諸性質コンボリューション たたみこみ積分 サンプリング定理 次元離散 次元空間周波数の概念 次元代表的な 次元対 次元離散 ベクトルの直交性 3
講義内容 講義内容 次元ベクトル 関数の直交性フーリエ級数 次元代表的な対の諸性質コンボリューション たたみこみ積分 サンプリング定理 次元離散 次元空間周波数の概念 次元代表的な 次元対 次元離散 次元ベクトル 関数の直交性フーリエ級数 次元代表的な対の諸性質コンボリューション たたみこみ積分 サンプリング定理 次元離散 次元空間周波数の概念 次元代表的な 次元対 次元離散 ベクトルの直交性 3
PowerPoint プレゼンテーション
 電磁波工学 第 5 回平面波の媒質への垂直および射入射と透過 柴田幸司 Bounda Plan Rgon ε μ Rgon Mdum ( ガラスなど ε μ z 平面波の反射と透過 垂直入射の場合 左図に示す様に 平面波が境界面に対して垂直に入射する場合を考える この時の入射波を とすると 入射波は境界において 透過波 と とに分解される この時の透過量を 反射量を Γ とおくと 領域 における媒質の誘電率に対して透過量
電磁波工学 第 5 回平面波の媒質への垂直および射入射と透過 柴田幸司 Bounda Plan Rgon ε μ Rgon Mdum ( ガラスなど ε μ z 平面波の反射と透過 垂直入射の場合 左図に示す様に 平面波が境界面に対して垂直に入射する場合を考える この時の入射波を とすると 入射波は境界において 透過波 と とに分解される この時の透過量を 反射量を Γ とおくと 領域 における媒質の誘電率に対して透過量
2009 年 11 月 16 日版 ( 久家 ) 遠地 P 波の変位波形の作成 遠地 P 波の変位波形 ( 変位の時間関数 ) は 波線理論をもとに P U () t = S()* t E()* t P() t で近似的に計算できる * は畳み込み積分 (convolution) を表す ( 付録
 遠地 波の変位波形の作成 遠地 波の変位波形 ( 変位の時間関数 ) は 波線理論をもとに U () t S() t E() t () t で近似的に計算できる は畳み込み積分 (convolution) を表す ( 付録 参照 ) ここで St () は地震の断層運動によって決まる時間関数 1 E() t は地下構造によって生じる種々の波の到着を与える時間関数 ( ここでは 直達 波とともに 震源そばの地表での反射波や変換波を与える時間関数
遠地 波の変位波形の作成 遠地 波の変位波形 ( 変位の時間関数 ) は 波線理論をもとに U () t S() t E() t () t で近似的に計算できる は畳み込み積分 (convolution) を表す ( 付録 参照 ) ここで St () は地震の断層運動によって決まる時間関数 1 E() t は地下構造によって生じる種々の波の到着を与える時間関数 ( ここでは 直達 波とともに 震源そばの地表での反射波や変換波を与える時間関数
Microsoft Word - 付録1誘導機の2軸理論.doc
 NAOSIE: Nagaaki Univity' Ac itl パワーエレクトロニクスと電動機制御入門 Autho( 辻, 峰男 Citation パワーエレクトロニクスと電動機制御入門 ; 15 Iu Dat 15 U http://hl.hanl.nt/169/55 ight hi ocumnt i ownloa http://naoit.lb.nagaaki-u.ac.jp 付録 1 誘導機の
NAOSIE: Nagaaki Univity' Ac itl パワーエレクトロニクスと電動機制御入門 Autho( 辻, 峰男 Citation パワーエレクトロニクスと電動機制御入門 ; 15 Iu Dat 15 U http://hl.hanl.nt/169/55 ight hi ocumnt i ownloa http://naoit.lb.nagaaki-u.ac.jp 付録 1 誘導機の
線積分.indd
 線積分 線積分 ( n, n, n ) (ξ n, η n, ζ n ) ( n-, n-, n- ) (ξ k, η k, ζ k ) ( k, k, k ) ( k-, k-, k- ) 物体に力 を作用させて位置ベクトル A の点 A から位置ベクトル の点 まで曲線 に沿って物体を移動させたときの仕事 W は 次式で計算された A, A, W : d 6 d+ d+ d@,,, d+ d+
線積分 線積分 ( n, n, n ) (ξ n, η n, ζ n ) ( n-, n-, n- ) (ξ k, η k, ζ k ) ( k, k, k ) ( k-, k-, k- ) 物体に力 を作用させて位置ベクトル A の点 A から位置ベクトル の点 まで曲線 に沿って物体を移動させたときの仕事 W は 次式で計算された A, A, W : d 6 d+ d+ d@,,, d+ d+
Chap2.key
 . f( ) V (V V ) V e + V e V V V V ( ) V V ( ) E. - () V (0 ) () V (0 ) () V (0 ) (4) V ( ) E. - () V (0 ) () V (0 ) O r θ ( ) ( ) : (r θ) : { r cos θ r sn θ { r + () V (0 ) (4) V ( ) θ θ arg( ) : π π
. f( ) V (V V ) V e + V e V V V V ( ) V V ( ) E. - () V (0 ) () V (0 ) () V (0 ) (4) V ( ) E. - () V (0 ) () V (0 ) O r θ ( ) ( ) : (r θ) : { r cos θ r sn θ { r + () V (0 ) (4) V ( ) θ θ arg( ) : π π
2015-2017年度 2次数学セレクション(複素数)解答解説
 05 次数学セレクション解答解説 [ 筑波大 ] ( + より, 0 となり, + から, ( (,, よって, の描く図形 C は, 点 を中心とし半径が の円である すなわち, 原 点を通る円となる ( は虚数, は正の実数より, である さて, w ( ( とおくと, ( ( ( w ( ( ( ここで, w は純虚数より, は純虚数となる すると, の描く図形 L は, 点 を通り, 点 と点
05 次数学セレクション解答解説 [ 筑波大 ] ( + より, 0 となり, + から, ( (,, よって, の描く図形 C は, 点 を中心とし半径が の円である すなわち, 原 点を通る円となる ( は虚数, は正の実数より, である さて, w ( ( とおくと, ( ( ( w ( ( ( ここで, w は純虚数より, は純虚数となる すると, の描く図形 L は, 点 を通り, 点 と点
2 Hermite-Gaussian モード 2-1 Hermite-Gaussian モード 自由空間を伝搬するレーザ光は次のような Hermite-gaussian Modes を持つ光波として扱う ことができる ここで U lm (x, y, z) U l (x, z)u m (y, z) e
 Wavefront Sensor 法による三角共振器のミスアラインメント検出 齊藤高大 新潟大学大学院自然科学研究科電気情報工学専攻博士後期課程 2 年 214 年 8 月 6 日 1 はじめに Input Mode Cleaner(IMC) は Fig.1 に示すような三角共振器である 懸架鏡の共振などにより IMC を構成する各ミラーが角度変化を起こすと 入射光軸と共振器軸との間にずれが生じる
Wavefront Sensor 法による三角共振器のミスアラインメント検出 齊藤高大 新潟大学大学院自然科学研究科電気情報工学専攻博士後期課程 2 年 214 年 8 月 6 日 1 はじめに Input Mode Cleaner(IMC) は Fig.1 に示すような三角共振器である 懸架鏡の共振などにより IMC を構成する各ミラーが角度変化を起こすと 入射光軸と共振器軸との間にずれが生じる
数学 t t t t t 加法定理 t t t 倍角公式加法定理で α=β と置く. 三角関数
 . 三角関数 基本関係 t cot c sc c cot sc t 還元公式 t t t t t t cot t cot t 数学 数学 t t t t t 加法定理 t t t 倍角公式加法定理で α=β と置く. 三角関数 数学. 三角関数 5 積和公式 6 和積公式 数学. 三角関数 7 合成 t V v t V v t V V V V VV V V V t V v v 8 べき乗 5 6 6
. 三角関数 基本関係 t cot c sc c cot sc t 還元公式 t t t t t t cot t cot t 数学 数学 t t t t t 加法定理 t t t 倍角公式加法定理で α=β と置く. 三角関数 数学. 三角関数 5 積和公式 6 和積公式 数学. 三角関数 7 合成 t V v t V v t V V V V VV V V V t V v v 8 べき乗 5 6 6
重要例題113
 04_ 高校 数学 Ⅱ 必須基本公式 定理集 数学 Ⅱ 第 章式の計算と方程式 0 商と余り についての整式 A をについての整式 B で割ったときの商を Q, 余りを R とすると, ABQ+R (R の次数 ) > 0
04_ 高校 数学 Ⅱ 必須基本公式 定理集 数学 Ⅱ 第 章式の計算と方程式 0 商と余り についての整式 A をについての整式 B で割ったときの商を Q, 余りを R とすると, ABQ+R (R の次数 ) > 0
人間科学部研究年報平成 24 年 (1) (2) (3) (4) 式 (1) は, クーロン (Coulomb) の法則とも呼ばれる.ρは電荷密度を表し,ε 0 は真空の誘電率と呼ばれる定数である. 式 (2) は, 磁荷が存在しないことを表す式である. 式 (3) はファラデー (Faraday)
 複素振幅をもつ球面波の人間科学部研究年報 Maxwell 平成 24 方程式年 複素振幅をもつ球面波の Maxwell 方程式 Maxwell Equation of Spherical Wave with Complex Amplitude 戸上良弘 Yoshihiro TOGAMI Abstract 複素振幅をもつ球面波に関して, マクスウェル (Maxwell) 方程式との関係を考察した. 電気的な球面波としてのスカラーポテンシャルが与えられたとき,
複素振幅をもつ球面波の人間科学部研究年報 Maxwell 平成 24 方程式年 複素振幅をもつ球面波の Maxwell 方程式 Maxwell Equation of Spherical Wave with Complex Amplitude 戸上良弘 Yoshihiro TOGAMI Abstract 複素振幅をもつ球面波に関して, マクスウェル (Maxwell) 方程式との関係を考察した. 電気的な球面波としてのスカラーポテンシャルが与えられたとき,
Microsoft Word - 微分入門.doc
 基本公式 例題 0 定義式 f( ) 数 Ⅲ 微分入門 = の導関数を定義式にもとづいて計算しなさい 基本事項 ( f( ), g( ) が微分可能ならば ) y= f( ) g( ) のとき, y = y= f( ) g( ) h( ) のとき, y = ( f( ), g( ) が微分可能で, g( ) 0 ならば ) f( ) y = のとき, y = g ( ) とくに, y = のとき,
基本公式 例題 0 定義式 f( ) 数 Ⅲ 微分入門 = の導関数を定義式にもとづいて計算しなさい 基本事項 ( f( ), g( ) が微分可能ならば ) y= f( ) g( ) のとき, y = y= f( ) g( ) h( ) のとき, y = ( f( ), g( ) が微分可能で, g( ) 0 ならば ) f( ) y = のとき, y = g ( ) とくに, y = のとき,
相対性理論入門 1 Lorentz 変換 光がどのような座標系に対しても同一の速さ c で進むことから導かれる座標の一次変換である. (x, y, z, t ) の座標系が (x, y, z, t) の座標系に対して x 軸方向に w の速度で進んでいる場合, 座標系が一次変換で関係づけられるとする
 相対性理論入門 Lorentz 変換 光がどのような座標系に対しても同一の速さ で進むことから導かれる座標の一次変換である. x, y, z, t ) の座標系が x, y, z, t) の座標系に対して x 軸方向に w の速度で進んでいる場合, 座標系が一次変換で関係づけられるとすると, x A x wt) y y z z t Bx + Dt 弨弱弩弨弲弩弨弳弩弨弴弩 が成立する. 図 : 相対速度
相対性理論入門 Lorentz 変換 光がどのような座標系に対しても同一の速さ で進むことから導かれる座標の一次変換である. x, y, z, t ) の座標系が x, y, z, t) の座標系に対して x 軸方向に w の速度で進んでいる場合, 座標系が一次変換で関係づけられるとすると, x A x wt) y y z z t Bx + Dt 弨弱弩弨弲弩弨弳弩弨弴弩 が成立する. 図 : 相対速度
複素数平面への誘い
 いざな複素数平面への誘い GRS による複素数平面の表現 複素数平面への第一歩 - 複素数モード - 点と複素数 -3 複素数の四則演算 -4 絶対値と偏角, 共役複素数 -5 絶対値と偏角による複素数の表現 複素数平面の変換 4 - 回転移動と相似拡大 - 直線 に関する対称変換 -3 単位円に関する反転変換 -4 複素数平面の変換と曲線 3 入試問題に挑戦 6 3- 陰関数を利用した図形の表示
いざな複素数平面への誘い GRS による複素数平面の表現 複素数平面への第一歩 - 複素数モード - 点と複素数 -3 複素数の四則演算 -4 絶対値と偏角, 共役複素数 -5 絶対値と偏角による複素数の表現 複素数平面の変換 4 - 回転移動と相似拡大 - 直線 に関する対称変換 -3 単位円に関する反転変換 -4 複素数平面の変換と曲線 3 入試問題に挑戦 6 3- 陰関数を利用した図形の表示
以下 変数の上のドットは時間に関する微分を表わしている (ex. 2 dx d x x, x 2 dt dt ) 付録 E 非線形微分方程式の平衡点の安定性解析 E-1) 非線形方程式の線形近似特に言及してこなかったが これまでは線形微分方程式 ( x や x, x などがすべて 1 次で なおかつ
 以下 変数の上のドットは時間に関する微分を表わしている (e. d d, dt dt ) 付録 E 非線形微分方程式の平衡点の安定性解析 E-) 非線形方程式の線形近似特に言及してこなかったが これまでは線形微分方程式 ( や, などがすべて 次で なおかつそれらの係数が定数であるような微分方程式 ) に対して安定性の解析を行ってきた しかしながら 実際には非線形の微分方程式で記述される現象も多く存在する
以下 変数の上のドットは時間に関する微分を表わしている (e. d d, dt dt ) 付録 E 非線形微分方程式の平衡点の安定性解析 E-) 非線形方程式の線形近似特に言及してこなかったが これまでは線形微分方程式 ( や, などがすべて 次で なおかつそれらの係数が定数であるような微分方程式 ) に対して安定性の解析を行ってきた しかしながら 実際には非線形の微分方程式で記述される現象も多く存在する
横浜市環境科学研究所
 周期時系列の統計解析 単回帰分析 io 8 年 3 日 周期時系列に季節調整を行わないで単回帰分析を適用すると, 回帰係数には周期成分の影響が加わる. ここでは, 周期時系列をコサイン関数モデルで近似し単回帰分析によりモデルの回帰係数を求め, 周期成分の影響を検討した. また, その結果を気温時系列に当てはめ, 課題等について考察した. 気温時系列とコサイン関数モデル第 報の結果を利用するので, その一部を再掲する.
周期時系列の統計解析 単回帰分析 io 8 年 3 日 周期時系列に季節調整を行わないで単回帰分析を適用すると, 回帰係数には周期成分の影響が加わる. ここでは, 周期時系列をコサイン関数モデルで近似し単回帰分析によりモデルの回帰係数を求め, 周期成分の影響を検討した. また, その結果を気温時系列に当てはめ, 課題等について考察した. 気温時系列とコサイン関数モデル第 報の結果を利用するので, その一部を再掲する.
多次元レーザー分光で探る凝縮分子系の超高速動力学
 波動方程式と量子力学 谷村吉隆 京都大学理学研究科化学専攻 http:theochem.kuchem.kyoto-u.ac.jp TA: 岩元佑樹 iwamoto.y@kuchem.kyoto-u.ac.jp ベクトルと行列の作法 A 列ベクトル c = c c 行ベクトル A = [ c c c ] 転置ベクトル T A = [ c c c ] AA 内積 c AA = [ c c c ] c =
波動方程式と量子力学 谷村吉隆 京都大学理学研究科化学専攻 http:theochem.kuchem.kyoto-u.ac.jp TA: 岩元佑樹 iwamoto.y@kuchem.kyoto-u.ac.jp ベクトルと行列の作法 A 列ベクトル c = c c 行ベクトル A = [ c c c ] 転置ベクトル T A = [ c c c ] AA 内積 c AA = [ c c c ] c =
<4D F736F F D20824F B CC92E8979D814696CA90CF95AA82C691CC90CF95AA2E646F63>
 1/1 平成 23 年 3 月 24 日午後 6 時 52 分 6 ガウスの定理 : 面積分と体積分 6 ガウスの定理 : 面積分と体積分 Ⅰ. 直交座標系 ガウスの定理は 微分して すぐに積分すると元に戻るというルールを 3 次元積分に適用した定理になります よく知っているのは 簡単化のため 変数が1つの場合は dj ( d ( ににします全微分 = 偏微分 d = d = J ( + C d です
1/1 平成 23 年 3 月 24 日午後 6 時 52 分 6 ガウスの定理 : 面積分と体積分 6 ガウスの定理 : 面積分と体積分 Ⅰ. 直交座標系 ガウスの定理は 微分して すぐに積分すると元に戻るというルールを 3 次元積分に適用した定理になります よく知っているのは 簡単化のため 変数が1つの場合は dj ( d ( ににします全微分 = 偏微分 d = d = J ( + C d です
Chap2
 逆三角関数の微分 Arcsin の導関数を計算する Arcsin I. 初等関数の微積分 sin [, ], [π/, π/] cos sin / (Arcsin ) 計算力の体力をつけよう π/ π/ E. II- 次の関数の導関数を計算せよ () Arccos () Arctan E. I- の解答 不定積分あれこれ () Arccos n log C C (n ) n e e C log (log
逆三角関数の微分 Arcsin の導関数を計算する Arcsin I. 初等関数の微積分 sin [, ], [π/, π/] cos sin / (Arcsin ) 計算力の体力をつけよう π/ π/ E. II- 次の関数の導関数を計算せよ () Arccos () Arctan E. I- の解答 不定積分あれこれ () Arccos n log C C (n ) n e e C log (log
Microsoft PowerPoint - 10.pptx
 0. 固有値とその応用 固有値と固有ベクトル 2 行列による写像から固有ベクトルへ m n A : m n n m 行列によって線形写像 f R R A が表せることを見てきた ここでは 2 次元平面の行列による写像を調べる 2 = 2 A 2 2 とし 写像 まず 単位ベクトルの像を求める u 2 x = v 2 y f : R A R を考える u 2 2 u, 2 2 0 = = v 2 0
0. 固有値とその応用 固有値と固有ベクトル 2 行列による写像から固有ベクトルへ m n A : m n n m 行列によって線形写像 f R R A が表せることを見てきた ここでは 2 次元平面の行列による写像を調べる 2 = 2 A 2 2 とし 写像 まず 単位ベクトルの像を求める u 2 x = v 2 y f : R A R を考える u 2 2 u, 2 2 0 = = v 2 0
0 21 カラー反射率 slope aspect 図 2.9: 復元結果例 2.4 画像生成技術としての計算フォトグラフィ 3 次元情報を復元することにより, 画像生成 ( レンダリング ) に応用することが可能である. 近年, コンピュータにより, カメラで直接得られない画像を生成する技術分野が生
 0 21 カラー反射率 slope aspect 図 2.9: 復元結果例 2.4 画像生成技術としての計算フォトグラフィ 3 次元情報を復元することにより, 画像生成 ( レンダリング ) に応用することが可能である. 近年, コンピュータにより, カメラで直接得られない画像を生成する技術分野が生まれ, コンピューテーショナルフォトグラフィ ( 計算フォトグラフィ ) と呼ばれている.3 次元画像認識技術の計算フォトグラフィへの応用として,
0 21 カラー反射率 slope aspect 図 2.9: 復元結果例 2.4 画像生成技術としての計算フォトグラフィ 3 次元情報を復元することにより, 画像生成 ( レンダリング ) に応用することが可能である. 近年, コンピュータにより, カメラで直接得られない画像を生成する技術分野が生まれ, コンピューテーショナルフォトグラフィ ( 計算フォトグラフィ ) と呼ばれている.3 次元画像認識技術の計算フォトグラフィへの応用として,
回転.rtf
 ベクトルの回転の定義は A A rot A ΔS 0 n ΔS (5.) : ounter dl 図 5. ベクトルの回転 であり, 回転量を調べる演算子である. ローテーションA, カールA,Aの回転とも読む. 図 5.のように, 閉曲線 に沿ってベクトル Aの線積分を行うものとする. 線積分はベクトル Aと線素 dl の内積だから, ある大きさ ( スカラー量 ) が得られる. その大きさをもち,
ベクトルの回転の定義は A A rot A ΔS 0 n ΔS (5.) : ounter dl 図 5. ベクトルの回転 であり, 回転量を調べる演算子である. ローテーションA, カールA,Aの回転とも読む. 図 5.のように, 閉曲線 に沿ってベクトル Aの線積分を行うものとする. 線積分はベクトル Aと線素 dl の内積だから, ある大きさ ( スカラー量 ) が得られる. その大きさをもち,
Microsoft PowerPoint - H22制御工学I-10回.ppt
 制御工学 I 第 回 安定性 ラウス, フルビッツの安定判別 平成 年 6 月 日 /6/ 授業の予定 制御工学概論 ( 回 ) 制御技術は現在様々な工学分野において重要な基本技術となっている 工学における制御工学の位置づけと歴史について説明する さらに 制御システムの基本構成と種類を紹介する ラプラス変換 ( 回 ) 制御工学 特に古典制御ではラプラス変換が重要な役割を果たしている ラプラス変換と逆ラプラス変換の定義を紹介し
制御工学 I 第 回 安定性 ラウス, フルビッツの安定判別 平成 年 6 月 日 /6/ 授業の予定 制御工学概論 ( 回 ) 制御技術は現在様々な工学分野において重要な基本技術となっている 工学における制御工学の位置づけと歴史について説明する さらに 制御システムの基本構成と種類を紹介する ラプラス変換 ( 回 ) 制御工学 特に古典制御ではラプラス変換が重要な役割を果たしている ラプラス変換と逆ラプラス変換の定義を紹介し
Microsoft Word - H26mse-bese-exp_no1.docx
 実験 No 電気回路の応答 交流回路とインピーダンスの計測 平成 26 年 4 月 担当教員 : 三宅 T A : 許斐 (M2) 齋藤 (M) 目的 2 世紀の社会において 電気エネルギーの占める割合は増加の一途をたどっている このような電気エネルギーを制御して使いこなすには その基礎となる電気回路をまず理解する必要がある 本実験の目的は 電気回路の基礎特性について 実験 計測を通じて理解を深めることである
実験 No 電気回路の応答 交流回路とインピーダンスの計測 平成 26 年 4 月 担当教員 : 三宅 T A : 許斐 (M2) 齋藤 (M) 目的 2 世紀の社会において 電気エネルギーの占める割合は増加の一途をたどっている このような電気エネルギーを制御して使いこなすには その基礎となる電気回路をまず理解する必要がある 本実験の目的は 電気回路の基礎特性について 実験 計測を通じて理解を深めることである
<4D F736F F D EBF97CD8A B7982D189898F4B A95748E9197BF4E6F31312E646F63>
 土質力学 Ⅰ 及び演習 (B 班 : 小高担当 ) 配付資料 N.11 (6.1.1) モールの応力円 (1) モールの応力円を使う上での3つの約束 1 垂直応力は圧縮を正とし, 軸の右側を正の方向とする 反時計まわりのモーメントを起こさせるせん断応力 の組を正とする 3 物体内で着目する面が,θ だけ回転すると, モールの応力円上では θ 回転する 1とは物理的な実際の作用面とモールの応力円上との回転の方向を一致させるために都合の良い約束である
土質力学 Ⅰ 及び演習 (B 班 : 小高担当 ) 配付資料 N.11 (6.1.1) モールの応力円 (1) モールの応力円を使う上での3つの約束 1 垂直応力は圧縮を正とし, 軸の右側を正の方向とする 反時計まわりのモーメントを起こさせるせん断応力 の組を正とする 3 物体内で着目する面が,θ だけ回転すると, モールの応力円上では θ 回転する 1とは物理的な実際の作用面とモールの応力円上との回転の方向を一致させるために都合の良い約束である
発散.rtf
 4 章発散 発散は重要なベクトル演算の一つであり, 定義は A =diva = lim Δv 0 Δv A d (4.) である.Divergence( ダイバージェンス ) ともいう. この意味は, 微小体積 vを取り囲む全表面 ( 閉曲面という ) 上で, 外向きのベクトル法線成分をすべて加えあわせ, 全体としての量を調べるものである. ベクトルAはどのような向きでもかまわないが, 面ベクトルとの内積
4 章発散 発散は重要なベクトル演算の一つであり, 定義は A =diva = lim Δv 0 Δv A d (4.) である.Divergence( ダイバージェンス ) ともいう. この意味は, 微小体積 vを取り囲む全表面 ( 閉曲面という ) 上で, 外向きのベクトル法線成分をすべて加えあわせ, 全体としての量を調べるものである. ベクトルAはどのような向きでもかまわないが, 面ベクトルとの内積
DVIOUT
 第 3 章 フーリエ変換 3.1 フーリエ積分とフーリエ変換 第 章では 周期を持つ関数のフーリエ級数について学びました この章では 最初に 周期を持つ関数のフーリエ級数を拡張し 周期を持たない ( 一般的な ) 関数のフーリエ級数を導きましょう 具体的には 関数 f(x) を区間 L x L で考え この L を限りなく大きくするというアプローチを取ります (L ) なお ここで扱う関数 f(x)
第 3 章 フーリエ変換 3.1 フーリエ積分とフーリエ変換 第 章では 周期を持つ関数のフーリエ級数について学びました この章では 最初に 周期を持つ関数のフーリエ級数を拡張し 周期を持たない ( 一般的な ) 関数のフーリエ級数を導きましょう 具体的には 関数 f(x) を区間 L x L で考え この L を限りなく大きくするというアプローチを取ります (L ) なお ここで扱う関数 f(x)
平成 30 年度入学試験問題 数学 注意事項試験開始後, 問題冊子及び解答用紙のページを確かめ, 落丁, 乱丁あるいは印刷が不鮮明なものがあれば新しいものと交換するので挙手すること 1. 試験開始の合図があるまで問題冊子を聞かないこと 試験開始後は, すべての解答用紙に受験番号 氏名を記入すること
 平成 30 年度入学試験問題 数学 注意事項試験開始後, 問題冊子及び解答用紙のページを確かめ, 落丁, 乱丁あるいは印刷が不鮮明なものがあれば新しいものと交換するので挙手すること 1. 試験開始の合図があるまで問題冊子を聞かないこと 試験開始後は, すべての解答用紙に受験番号 氏名を記入すること 各志願者は, 下の表 に指示した問題を解答すること ただし, 教育学部に ついては志望するコース (
平成 30 年度入学試験問題 数学 注意事項試験開始後, 問題冊子及び解答用紙のページを確かめ, 落丁, 乱丁あるいは印刷が不鮮明なものがあれば新しいものと交換するので挙手すること 1. 試験開始の合図があるまで問題冊子を聞かないこと 試験開始後は, すべての解答用紙に受験番号 氏名を記入すること 各志願者は, 下の表 に指示した問題を解答すること ただし, 教育学部に ついては志望するコース (
学習指導要領
 (1) 数と式 ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 絶対値の意味を理解し適切な処理することができる 例題 1-3 の絶対値をはずせ 展開公式 ( a + b ) ( a - b ) = a 2 - b 2 を利用して根号を含む分数の分母を有理化することができる 例題 5 5 + 2 の分母を有理化せよ 実数の整数部分と小数部分の表し方を理解している
(1) 数と式 ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 絶対値の意味を理解し適切な処理することができる 例題 1-3 の絶対値をはずせ 展開公式 ( a + b ) ( a - b ) = a 2 - b 2 を利用して根号を含む分数の分母を有理化することができる 例題 5 5 + 2 の分母を有理化せよ 実数の整数部分と小数部分の表し方を理解している
数値計算で学ぶ物理学 4 放物運動と惑星運動 地上のように下向きに重力がはたらいているような場においては 物体を投げると放物運動をする 一方 中心星のまわりの重力場中では 惑星は 円 だ円 放物線または双曲線を描きながら運動する ここでは 放物運動と惑星運動を 運動方程式を導出したうえで 数値シミュ
 数値計算で学ぶ物理学 4 放物運動と惑星運動 地上のように下向きに重力がはたらいているような場においては 物体を投げると放物運動をする 一方 中心星のまわりの重力場中では 惑星は 円 だ円 放物線または双曲線を描きながら運動する ここでは 放物運動と惑星運動を 運動方程式を導出したうえで 数値シミュレーションによって計算してみる 4.1 放物運動一様な重力場における放物運動を考える 一般に質量の物体に作用する力をとすると運動方程式は
数値計算で学ぶ物理学 4 放物運動と惑星運動 地上のように下向きに重力がはたらいているような場においては 物体を投げると放物運動をする 一方 中心星のまわりの重力場中では 惑星は 円 だ円 放物線または双曲線を描きながら運動する ここでは 放物運動と惑星運動を 運動方程式を導出したうえで 数値シミュレーションによって計算してみる 4.1 放物運動一様な重力場における放物運動を考える 一般に質量の物体に作用する力をとすると運動方程式は
2018年度 筑波大・理系数学
 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ < < とする 放物線 上に 点 (, ), A (ta, ta ), B( - ta, ta ) をとる 三角形 AB の内心の 座標を p とし, 外心の 座標を q とする また, 正の実数 a に対して, 直線 a と放物線 で囲まれた図形の面積を S( a) で表す () p, q を cos を用いて表せ S( p) () S(
筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ < < とする 放物線 上に 点 (, ), A (ta, ta ), B( - ta, ta ) をとる 三角形 AB の内心の 座標を p とし, 外心の 座標を q とする また, 正の実数 a に対して, 直線 a と放物線 で囲まれた図形の面積を S( a) で表す () p, q を cos を用いて表せ S( p) () S(
平成 年 月 7 日 ( 土 第 75 回数学教育実践研究会アスティ 45 ビル F セミナールーム A 札幌医科大学 年 P ab, を正の定数とする 平面上において ( a, を中心とする円 Q 4 C と (, b を中心とする円 C が 原点 O で外接している また P を円 C 上の点と
 平成 年 月 7 日 ( 土 第 75 回数学教育実践研究会アスティ 45 ビル F セミナールーム 微分積分の拡張 変数関数問題へのアプローチ 予選決勝優勝法からラグランジュ未定乗数法 松本睦郎 ( 札幌北高等学校 変数関数の最大値 最小値に関する問題には多様なアプローチ法がある 文字を固定した 予選決勝優勝法, 計算のみで解法する 文字消去法, 微分積分を利用した ラグランジュ未定乗数法 がある
平成 年 月 7 日 ( 土 第 75 回数学教育実践研究会アスティ 45 ビル F セミナールーム 微分積分の拡張 変数関数問題へのアプローチ 予選決勝優勝法からラグランジュ未定乗数法 松本睦郎 ( 札幌北高等学校 変数関数の最大値 最小値に関する問題には多様なアプローチ法がある 文字を固定した 予選決勝優勝法, 計算のみで解法する 文字消去法, 微分積分を利用した ラグランジュ未定乗数法 がある
DVIOUT-17syoze
 平面の合同変換と相似変換 岩瀬順一 要約 : 平面の合同変換と相似変換を論じる いま大学で行列を学び始めている大学一年生を念頭に置いている 高等学校で行列や一次変換を学んでいなくてもよい 1. 写像 定義 1.1 X, Y を集合とする X の各元 x に対し Y のただ一つの元 y を対応させる規則 f を写像とよび,f : X! Y のように書く f によって x に対応する Y の元を f(x)
平面の合同変換と相似変換 岩瀬順一 要約 : 平面の合同変換と相似変換を論じる いま大学で行列を学び始めている大学一年生を念頭に置いている 高等学校で行列や一次変換を学んでいなくてもよい 1. 写像 定義 1.1 X, Y を集合とする X の各元 x に対し Y のただ一つの元 y を対応させる規則 f を写像とよび,f : X! Y のように書く f によって x に対応する Y の元を f(x)
学力スタンダード(様式1)
 (1) 数と式 学習指導要領ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 稔ヶ丘高校学力スタンダード 有理数 無理数の定義や実数の分類について理解し ている 絶対値の意味と記号表示を理解している 実数と直線上の点が一対一対応であることを理解 し 実数を数直線上に示すことができる 例 実数 (1) -.5 () π (3) 数直線上の点はどれか答えよ
(1) 数と式 学習指導要領ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 稔ヶ丘高校学力スタンダード 有理数 無理数の定義や実数の分類について理解し ている 絶対値の意味と記号表示を理解している 実数と直線上の点が一対一対応であることを理解 し 実数を数直線上に示すことができる 例 実数 (1) -.5 () π (3) 数直線上の点はどれか答えよ
Microsoft PowerPoint - 9.pptx
 9. 線形写像 ここでは 行列の積によって 写像を定義できることをみていく また 行列の積によって定義される写像の性質を調べていく 行列演算と写像 ( 次変換 3 拡大とスカラー倍 p ' = ( ', ' = ( k, kk p = (, k 倍 k 倍 拡大後 k 倍拡大の関係は スカラー倍を用いて次のように表現できる ' = k ' 拡大前 拡大 4 拡大と行列の積 p ' = ( ', '
9. 線形写像 ここでは 行列の積によって 写像を定義できることをみていく また 行列の積によって定義される写像の性質を調べていく 行列演算と写像 ( 次変換 3 拡大とスカラー倍 p ' = ( ', ' = ( k, kk p = (, k 倍 k 倍 拡大後 k 倍拡大の関係は スカラー倍を用いて次のように表現できる ' = k ' 拡大前 拡大 4 拡大と行列の積 p ' = ( ', '
<4D F736F F D F2095A F795AA B B A815B837D839382CC95FB92F68EAE2E646F63>
 1/8 平成 3 年 3 月 4 日午後 6 時 11 分 10 複素微分 : コーシー リーマンの方程式 10 複素微分 : コーシー リーマンの方程式 9 複素微分 : 正則関数 で 正則性は複素数 z の関数 f ( z) の性質として導き出しまし た 複素数 z は つの実数, で表され z i 数 u, v で表され f ( z) u i 複素数 z と つの実数, : z + i + です
1/8 平成 3 年 3 月 4 日午後 6 時 11 分 10 複素微分 : コーシー リーマンの方程式 10 複素微分 : コーシー リーマンの方程式 9 複素微分 : 正則関数 で 正則性は複素数 z の関数 f ( z) の性質として導き出しまし た 複素数 z は つの実数, で表され z i 数 u, v で表され f ( z) u i 複素数 z と つの実数, : z + i + です
受信機時計誤差項の が残ったままであるが これをも消去するのが 重位相差である. 重位相差ある時刻に 衛星 から送られてくる搬送波位相データを 台の受信機 でそれぞれ測定する このとき各受信機で測定された衛星 からの搬送波位相データを Φ Φ とし 同様に衛星 からの搬送波位相データを Φ Φ とす
 RTK-GPS 測位計算アルゴリズム -FLOT 解 - 東京海洋大学冨永貴樹. はじめに GPS 測量を行う際 実時間で測位結果を得ることが出来るのは今のところ RTK-GPS 測位のみである GPS 測量では GPS 衛星からの搬送波位相データを使用するため 整数値バイアスを決定しなければならず これが測位計算を複雑にしている所以である この整数値バイアスを決定するためのつの方法として FLOT
RTK-GPS 測位計算アルゴリズム -FLOT 解 - 東京海洋大学冨永貴樹. はじめに GPS 測量を行う際 実時間で測位結果を得ることが出来るのは今のところ RTK-GPS 測位のみである GPS 測量では GPS 衛星からの搬送波位相データを使用するため 整数値バイアスを決定しなければならず これが測位計算を複雑にしている所以である この整数値バイアスを決定するためのつの方法として FLOT
Microsoft Word - 1B2011.doc
 第 14 回モールの定理 ( 単純梁の場合 ) ( モールの定理とは何か?p.11) 例題 下記に示す単純梁の C 点のたわみ角 θ C と, たわみ δ C を求めよ ただし, 部材の曲げ 剛性は材軸に沿って一様で とする C D kn B 1.5m 0.5m 1.0m 解答 1 曲げモーメント図を描く,B 点の反力を求める kn kn 4 kn 曲げモーメント図を描く knm 先に得られた曲げモーメントの値を
第 14 回モールの定理 ( 単純梁の場合 ) ( モールの定理とは何か?p.11) 例題 下記に示す単純梁の C 点のたわみ角 θ C と, たわみ δ C を求めよ ただし, 部材の曲げ 剛性は材軸に沿って一様で とする C D kn B 1.5m 0.5m 1.0m 解答 1 曲げモーメント図を描く,B 点の反力を求める kn kn 4 kn 曲げモーメント図を描く knm 先に得られた曲げモーメントの値を
1/17 平成 29 年 3 月 25 日 ( 土 ) 午前 11 時 1 分量子力学とクライン ゴルドン方程式 ( 学部 3 年次秋学期向 ) 量子力学とクライン ゴルドン方程式 素粒子の満たす場 y ( x,t) の運動方程式 : クライン ゴルドン方程式 : æ 3 ö ç å è m= 0
 /7 平成 9 年 月 5 日 ( 土 午前 時 分量子力学とクライン ゴルドン方程式 ( 学部 年次秋学期向 量子力学とクライン ゴルドン方程式 素粒子の満たす場 (,t の運動方程式 : クライン ゴルドン方程式 : æ ö ç å è = 0 c + ( t =, 0 (. = 0 ì æ = = = ö æ ö æ ö ç ì =,,,,,,, ç 0 = ç Ñ 0 = ç Ñ 0 Ñ Ñ
/7 平成 9 年 月 5 日 ( 土 午前 時 分量子力学とクライン ゴルドン方程式 ( 学部 年次秋学期向 量子力学とクライン ゴルドン方程式 素粒子の満たす場 (,t の運動方程式 : クライン ゴルドン方程式 : æ ö ç å è = 0 c + ( t =, 0 (. = 0 ì æ = = = ö æ ö æ ö ç ì =,,,,,,, ç 0 = ç Ñ 0 = ç Ñ 0 Ñ Ñ
Microsoft Word - 201hyouka-tangen-1.doc
 数学 Ⅰ 評価規準の作成 ( 単元ごと ) 数学 Ⅰ の目標及び図形と計量について理解させ 基礎的な知識の習得と技能の習熟を図り それらを的確に活用する機能を伸ばすとともに 数学的な見方や考え方のよさを認識できるようにする 評価の観点の趣旨 式と不等式 二次関数及び図形と計量における考え方に関 心をもつとともに 数学的な見方や考え方のよさを認識し それらを事象の考察に活用しようとする 式と不等式 二次関数及び図形と計量における数学的な見
数学 Ⅰ 評価規準の作成 ( 単元ごと ) 数学 Ⅰ の目標及び図形と計量について理解させ 基礎的な知識の習得と技能の習熟を図り それらを的確に活用する機能を伸ばすとともに 数学的な見方や考え方のよさを認識できるようにする 評価の観点の趣旨 式と不等式 二次関数及び図形と計量における考え方に関 心をもつとともに 数学的な見方や考え方のよさを認識し それらを事象の考察に活用しようとする 式と不等式 二次関数及び図形と計量における数学的な見
2 図微小要素の流体の流入出 方向の断面の流体の流入出の収支断面 Ⅰ から微小要素に流入出する流体の流量 Q 断面 Ⅰ は 以下のように定式化できる Q 断面 Ⅰ 流量 密度 流速 断面 Ⅰ の面積 微小要素の断面 Ⅰ から だけ移動した断面 Ⅱ を流入出する流体の流量 Q 断面 Ⅱ は以下のように
 3 章 Web に Link 解説 連続式 微分表示 の誘導.64 *4. 連続式連続式は ある領域の内部にある流体の質量の収支が その表面からの流入出の合計と等しくなることを定式化したものであり 流体における質量保存則を示したものである 2. 連続式 微分表示 の誘導図のような微小要素 コントロールボリューム の領域内の流体の増減と外部からの流体の流入出を考えることで定式化できる 微小要素 流入
3 章 Web に Link 解説 連続式 微分表示 の誘導.64 *4. 連続式連続式は ある領域の内部にある流体の質量の収支が その表面からの流入出の合計と等しくなることを定式化したものであり 流体における質量保存則を示したものである 2. 連続式 微分表示 の誘導図のような微小要素 コントロールボリューム の領域内の流体の増減と外部からの流体の流入出を考えることで定式化できる 微小要素 流入
画像処理工学
 画像処理工学 画像の空間周波数解析とテクスチャ特徴 フーリエ変換の基本概念 信号波形のフーリエ変換 信号波形を周波数の異なる三角関数 ( 正弦波など ) に分解する 逆に, 周波数の異なる三角関数を重ねあわせることにより, 任意の信号波形を合成できる 正弦波の重ね合わせによる矩形波の表現 フーリエ変換の基本概念 フーリエ変換 次元信号 f (t) のフーリエ変換 変換 ( ω) ( ) ωt F f
画像処理工学 画像の空間周波数解析とテクスチャ特徴 フーリエ変換の基本概念 信号波形のフーリエ変換 信号波形を周波数の異なる三角関数 ( 正弦波など ) に分解する 逆に, 周波数の異なる三角関数を重ねあわせることにより, 任意の信号波形を合成できる 正弦波の重ね合わせによる矩形波の表現 フーリエ変換の基本概念 フーリエ変換 次元信号 f (t) のフーリエ変換 変換 ( ω) ( ) ωt F f
2018年度 東京大・理系数学
 08 東京大学 ( 理系 ) 前期日程問題 解答解説のページへ関数 f ( ) = + cos (0 < < ) の増減表をつくり, + 0, 0 のと sin きの極限を調べよ 08 東京大学 ( 理系 ) 前期日程問題 解答解説のページへ n+ 数列 a, a, を, Cn a n = ( n =,, ) で定める n! an qn () n とする を既約分数 an p として表したときの分母
08 東京大学 ( 理系 ) 前期日程問題 解答解説のページへ関数 f ( ) = + cos (0 < < ) の増減表をつくり, + 0, 0 のと sin きの極限を調べよ 08 東京大学 ( 理系 ) 前期日程問題 解答解説のページへ n+ 数列 a, a, を, Cn a n = ( n =,, ) で定める n! an qn () n とする を既約分数 an p として表したときの分母
Microsoft PowerPoint - ロボットの運動学forUpload'C5Q [互換モード]
![Microsoft PowerPoint - ロボットの運動学forUpload'C5Q [互換モード] Microsoft PowerPoint - ロボットの運動学forUpload'C5Q [互換モード]](/thumbs/104/163308363.jpg) ロボットの運動学 順運動学とは 座標系の回転と並進 同次座標変換行列 Denavit-Hartenberg の表記法 多関節ロボットの順運動学 レポート課題 & 中間試験について 逆運動学とは ヤコビアン行列 運動方程式 ( 微分方程式 ) ロボットの運動学 動力学 Equation of motion f ( ( t), ( t), ( t)) τ( t) 姿勢 ( 関節角の組合せ ) Posture
ロボットの運動学 順運動学とは 座標系の回転と並進 同次座標変換行列 Denavit-Hartenberg の表記法 多関節ロボットの順運動学 レポート課題 & 中間試験について 逆運動学とは ヤコビアン行列 運動方程式 ( 微分方程式 ) ロボットの運動学 動力学 Equation of motion f ( ( t), ( t), ( t)) τ( t) 姿勢 ( 関節角の組合せ ) Posture
1/30 平成 29 年 3 月 24 日 ( 金 ) 午前 11 時 25 分第三章フェルミ量子場 : スピノール場 ( 次元あり ) 第三章フェルミ量子場 : スピノール場 フェルミ型 ボーズ量子場のエネルギーは 第二章ボーズ量子場 : スカラー場 の (2.18) より ˆ dp 1 1 =
 / 平成 9 年 月 日 ( 金 午前 時 5 分第三章フェルミ量子場 : スピノール場 ( 次元あり 第三章フェルミ量子場 : スピノール場 フェルミ型 ボーズ量子場のエネルギーは 第二章ボーズ量子場 : スカラー場 の (.8 より ˆ ( ( ( q -, ( ( c ( H c c ë é ù û - Ü + c ( ( - に限る (. である 一方 フェルミ型は 成分をもち その成分を,,,,
/ 平成 9 年 月 日 ( 金 午前 時 5 分第三章フェルミ量子場 : スピノール場 ( 次元あり 第三章フェルミ量子場 : スピノール場 フェルミ型 ボーズ量子場のエネルギーは 第二章ボーズ量子場 : スカラー場 の (.8 より ˆ ( ( ( q -, ( ( c ( H c c ë é ù û - Ü + c ( ( - に限る (. である 一方 フェルミ型は 成分をもち その成分を,,,,
SPring-8ワークショップ_リガク伊藤
 GI SAXS. X X X X GI-SAXS : Grazing-incidence smallangle X-ray scattering. GI-SAXS GI-SAXS GI-SAXS X X X X X GI-SAXS Q Y : Q Z : Q Y - Q Z CCD Charge-coupled device X X APD Avalanche photo diode - cps 8
GI SAXS. X X X X GI-SAXS : Grazing-incidence smallangle X-ray scattering. GI-SAXS GI-SAXS GI-SAXS X X X X X GI-SAXS Q Y : Q Z : Q Y - Q Z CCD Charge-coupled device X X APD Avalanche photo diode - cps 8
線形代数とは
 線形代数とは 第一回ベクトル 教科書 エクササイズ線形代数 立花俊一 成田清正著 共立出版 必要最低限のことに限る 得意な人には物足りないかもしれません 線形代数とは何をするもの? 線形関係 y 直線 yもも 次式で登場する (( 次の形 ) 線形 ただし 次元の話世の中は 3 次元 [4[ 次元 ] 次元 3 次元 4 次元 はどうやって直線を表すの? ベクトルや行列の概念 y A ベクトルを使うと
線形代数とは 第一回ベクトル 教科書 エクササイズ線形代数 立花俊一 成田清正著 共立出版 必要最低限のことに限る 得意な人には物足りないかもしれません 線形代数とは何をするもの? 線形関係 y 直線 yもも 次式で登場する (( 次の形 ) 線形 ただし 次元の話世の中は 3 次元 [4[ 次元 ] 次元 3 次元 4 次元 はどうやって直線を表すの? ベクトルや行列の概念 y A ベクトルを使うと
スライド 1
 暫定版修正 加筆の可能性あり ( 付録 ) 電磁波 ( 光 ) の角運動量. 復習 : 電磁波 ( 光 ) のエネルギー. 運動量 角運動量 ( 実空間 ) 3. 軌道 スピン角運動量 4. 円偏光状態 5. 螺旋状態 付録 8 のアプローチ. 本付録では電磁波 ( 光 ) の軌道 スピン角運動量ついて古典的に扱う. スピン角運動量は直線偏光状態では零 円偏光状態では非零 右 左回りで大きさは同じ
暫定版修正 加筆の可能性あり ( 付録 ) 電磁波 ( 光 ) の角運動量. 復習 : 電磁波 ( 光 ) のエネルギー. 運動量 角運動量 ( 実空間 ) 3. 軌道 スピン角運動量 4. 円偏光状態 5. 螺旋状態 付録 8 のアプローチ. 本付録では電磁波 ( 光 ) の軌道 スピン角運動量ついて古典的に扱う. スピン角運動量は直線偏光状態では零 円偏光状態では非零 右 左回りで大きさは同じ
s とは何か 2011 年 2 月 5 日目次へ戻る 1 正弦波の微分 y=v m sin ωt を時間 t で微分します V m は正弦波の最大値です 合成関数の微分法を用い y=v m sin u u=ωt と置きますと dy dt dy du du dt d du V m sin u d dt
 とは何か 0 年 月 5 日目次へ戻る 正弦波の微分 y= in を時間 で微分します は正弦波の最大値です 合成関数の微分法を用い y= in u u= と置きますと y y in u in u (co u co になります in u の は定数なので 微分後も残ります 合成関数の微分法ですので 最後に u を に戻しています 0[ra] の co 値は [ra] の in 値と同じです その先の角
とは何か 0 年 月 5 日目次へ戻る 正弦波の微分 y= in を時間 で微分します は正弦波の最大値です 合成関数の微分法を用い y= in u u= と置きますと y y in u in u (co u co になります in u の は定数なので 微分後も残ります 合成関数の微分法ですので 最後に u を に戻しています 0[ra] の co 値は [ra] の in 値と同じです その先の角
Microsoft PowerPoint - 9.pptx
 9/7/8( 水 9. 線形写像 ここでは 行列の積によって 写像を定義できることをみていく また 行列の積によって定義される写像の性質を調べていく 拡大とスカラー倍 行列演算と写像 ( 次変換 拡大後 k 倍 k 倍 k 倍拡大の関係は スカラー倍を用いて次のように表現できる p = (, ' = k ' 拡大前 p ' = ( ', ' = ( k, k 拡大 4 拡大と行列の積 拡大後 k 倍
9/7/8( 水 9. 線形写像 ここでは 行列の積によって 写像を定義できることをみていく また 行列の積によって定義される写像の性質を調べていく 拡大とスカラー倍 行列演算と写像 ( 次変換 拡大後 k 倍 k 倍 k 倍拡大の関係は スカラー倍を用いて次のように表現できる p = (, ' = k ' 拡大前 p ' = ( ', ' = ( k, k 拡大 4 拡大と行列の積 拡大後 k 倍
学習指導要領
 (1 ) 数と式 ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 自然数 整数 有理数 無理数の包含関係など 実 数の構成を理解する ( 例 ) 次の空欄に適当な言葉をいれて, 数の集合を表しなさい 実数の絶対値が実数と対応する点と原点との距離で あることを理解する ( 例 ) 次の値を求めよ (1) () 6 置き換えなどを利用して 三項の無理数の乗法の計
(1 ) 数と式 ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 自然数 整数 有理数 無理数の包含関係など 実 数の構成を理解する ( 例 ) 次の空欄に適当な言葉をいれて, 数の集合を表しなさい 実数の絶対値が実数と対応する点と原点との距離で あることを理解する ( 例 ) 次の値を求めよ (1) () 6 置き換えなどを利用して 三項の無理数の乗法の計
Laplace2.rtf
 =0 ラプラスの方程式は 階の微分方程式で, 一般的に3つの座標変数をもつ. ここでは, 直角座標系, 円筒座標系, 球座標系におけるラプラスの方程式の解き方を説明しよう. 座標変数ごとに方程式を分離し, それを解いていく方法は変数分離法と呼ばれる. 変数分離解と固有関数展開法. 直角座標系における 3 次元の偏微分方程式 = x + y + z =0 (.) を解くために,x, y, z について互いに独立な関数の積で成り立っていると考え,
=0 ラプラスの方程式は 階の微分方程式で, 一般的に3つの座標変数をもつ. ここでは, 直角座標系, 円筒座標系, 球座標系におけるラプラスの方程式の解き方を説明しよう. 座標変数ごとに方程式を分離し, それを解いていく方法は変数分離法と呼ばれる. 変数分離解と固有関数展開法. 直角座標系における 3 次元の偏微分方程式 = x + y + z =0 (.) を解くために,x, y, z について互いに独立な関数の積で成り立っていると考え,
様々なミクロ計量モデル†
 担当 : 長倉大輔 ( ながくらだいすけ ) この資料は私の講義において使用するために作成した資料です WEB ページ上で公開しており 自由に参照して頂いて構いません ただし 内容について 一応検証してありますが もし間違いがあった場合でもそれによって生じるいかなる損害 不利益について責任を負いかねますのでご了承ください 間違いは発見次第 継続的に直していますが まだ存在する可能性があります 1 カウントデータモデル
担当 : 長倉大輔 ( ながくらだいすけ ) この資料は私の講義において使用するために作成した資料です WEB ページ上で公開しており 自由に参照して頂いて構いません ただし 内容について 一応検証してありますが もし間違いがあった場合でもそれによって生じるいかなる損害 不利益について責任を負いかねますのでご了承ください 間違いは発見次第 継続的に直していますが まだ存在する可能性があります 1 カウントデータモデル
Microsoft Word - Chap17
 第 7 章化学反応に対する磁場効果における三重項機構 その 7.. 節の訂正 年 7 月 日. 節 章の9ページ の赤枠に記載した説明は間違いであった事に気付いた 以下に訂正する しかし.. 式は 結果的には正しいので安心して下さい 磁場 の存在下でのT 状態のハミルトニアン は ゼーマン項 と時間に依存するスピン-スピン相互作用の項 との和となる..=7.. g S = g S z = S z g
第 7 章化学反応に対する磁場効果における三重項機構 その 7.. 節の訂正 年 7 月 日. 節 章の9ページ の赤枠に記載した説明は間違いであった事に気付いた 以下に訂正する しかし.. 式は 結果的には正しいので安心して下さい 磁場 の存在下でのT 状態のハミルトニアン は ゼーマン項 と時間に依存するスピン-スピン相互作用の項 との和となる..=7.. g S = g S z = S z g
機構学 平面機構の運動学
 問題 1 静止座標系 - 平面上を運動する節 b 上に2 定点,Bを考える. いま,2 点の座標は(0,0),B(50,0) である. 2 点間の距離は 50 mm, 点の速度が a 150 mm/s, 点 Bの速度の向きが150 である. 以下の問いに答えよ. (1) 点 Bの速度を求めよ. (2) 瞬間中心を求めよ. 節 b a (0,0) b 150 B(50,0) 問題 1(1) 解答 b
問題 1 静止座標系 - 平面上を運動する節 b 上に2 定点,Bを考える. いま,2 点の座標は(0,0),B(50,0) である. 2 点間の距離は 50 mm, 点の速度が a 150 mm/s, 点 Bの速度の向きが150 である. 以下の問いに答えよ. (1) 点 Bの速度を求めよ. (2) 瞬間中心を求めよ. 節 b a (0,0) b 150 B(50,0) 問題 1(1) 解答 b
2011年度 大阪大・理系数学
 0 大阪大学 ( 理系 ) 前期日程問題 解答解説のページへ a a を自然数とする O を原点とする座標平面上で行列 A= a の表す 次変換 を f とする cosθ siθ () >0 および0θ
0 大阪大学 ( 理系 ) 前期日程問題 解答解説のページへ a a を自然数とする O を原点とする座標平面上で行列 A= a の表す 次変換 を f とする cosθ siθ () >0 および0θ
DVIOUT
 1 体積 1.1 初めに この中では積分は第一基本量 ( 微分幾何 ) を用いて計算する 基本量の 意味を知らなくても別に気にする必要はなく 計算をたどって行けば理解 できるように書いてある 計算するものは球の体積なので カルテシアン 座標 (x-y 座標の畏まった言い方 ) ではなく 球座標を用いるようになる 球座標も x-y 座標と同様に直交座標であるので 扱うのに便利である 通 常は体積などを計算するために座標変換すると
1 体積 1.1 初めに この中では積分は第一基本量 ( 微分幾何 ) を用いて計算する 基本量の 意味を知らなくても別に気にする必要はなく 計算をたどって行けば理解 できるように書いてある 計算するものは球の体積なので カルテシアン 座標 (x-y 座標の畏まった言い方 ) ではなく 球座標を用いるようになる 球座標も x-y 座標と同様に直交座標であるので 扱うのに便利である 通 常は体積などを計算するために座標変換すると
学習指導要領
 (1) 数と式 学習指導要領 数と式 (1) 式の計算二次の乗法公式及び因数分解の公式の理解を深め 式を多面的にみたり目的に応じて式を適切に変形したりすること 東京都立町田高等学校学力スタンダード 整式の加法 減法 乗法展開の公式を利用できる 式を1 つの文字におき換えることによって, 式の計算を簡略化することができる 式の形の特徴に着目して変形し, 展開の公式が適用できるようにすることができる 因数分解因数分解の公式を利用できる
(1) 数と式 学習指導要領 数と式 (1) 式の計算二次の乗法公式及び因数分解の公式の理解を深め 式を多面的にみたり目的に応じて式を適切に変形したりすること 東京都立町田高等学校学力スタンダード 整式の加法 減法 乗法展開の公式を利用できる 式を1 つの文字におき換えることによって, 式の計算を簡略化することができる 式の形の特徴に着目して変形し, 展開の公式が適用できるようにすることができる 因数分解因数分解の公式を利用できる
破壊の予測
 本日の講義内容 前提 : 微分積分 線形代数が何をしているかはうろ覚え 材料力学は勉強したけど ちょっと 弾性および塑性学は勉強したことが無い ー > ですので 解らないときは質問してください モールの応力円を理解するとともに 応力を 3 次元的に考える FM( 有限要素法 の概略 内部では何を計算しているのか? 3 物が壊れる条件を考える 特に 変形 ( 塑性変形 が発生する条件としてのミーゼス応力とはどのような応力か?
本日の講義内容 前提 : 微分積分 線形代数が何をしているかはうろ覚え 材料力学は勉強したけど ちょっと 弾性および塑性学は勉強したことが無い ー > ですので 解らないときは質問してください モールの応力円を理解するとともに 応力を 3 次元的に考える FM( 有限要素法 の概略 内部では何を計算しているのか? 3 物が壊れる条件を考える 特に 変形 ( 塑性変形 が発生する条件としてのミーゼス応力とはどのような応力か?
<8D828D5A838A817C A77425F91E6318FCD2E6D6364>
 4 1 平面上のベクトル 1 ベクトルとその演算 例題 1 ベクトルの相等 次の問いに答えよ. ⑴ 右の図 1 は平行四辺形 である., と等しいベクトルをいえ. ⑵ 右の図 2 の中で互いに等しいベクトルをいえ. ただし, すべてのマス目は正方形である. 解 ⑴,= より, =,= より, = ⑵ 大きさと向きの等しいものを調べる. a =d, c = f d e f 1 右の図の長方形 において,
4 1 平面上のベクトル 1 ベクトルとその演算 例題 1 ベクトルの相等 次の問いに答えよ. ⑴ 右の図 1 は平行四辺形 である., と等しいベクトルをいえ. ⑵ 右の図 2 の中で互いに等しいベクトルをいえ. ただし, すべてのマス目は正方形である. 解 ⑴,= より, =,= より, = ⑵ 大きさと向きの等しいものを調べる. a =d, c = f d e f 1 右の図の長方形 において,
PoincareDisk-3.doc
 3. ポアンカレ円盤上の 次分数変換この節以降では, 単に双曲的直線, 双曲的円などといえば, 全てポアンカレ円盤上の基本図形とします. また, 点 と点 B のポアンカレ円盤上での双曲的距離を,[,B] と表します. 3. 双曲的垂直 等分線 ユークリッドの原論 において 円 双曲的円, 直線 双曲的直線 の置き換えを行うだけで, 双曲的垂直 等分線, 双曲的内心, 双曲的外心などを 機械的に (
3. ポアンカレ円盤上の 次分数変換この節以降では, 単に双曲的直線, 双曲的円などといえば, 全てポアンカレ円盤上の基本図形とします. また, 点 と点 B のポアンカレ円盤上での双曲的距離を,[,B] と表します. 3. 双曲的垂直 等分線 ユークリッドの原論 において 円 双曲的円, 直線 双曲的直線 の置き換えを行うだけで, 双曲的垂直 等分線, 双曲的内心, 双曲的外心などを 機械的に (
ディジタル信号処理
 ディジタルフィルタの設計法. 逆フィルター. 直線位相 FIR フィルタの設計. 窓関数法による FIR フィルタの設計.5 時間領域での FIR フィルタの設計 3. アナログフィルタを基にしたディジタル IIR フィルタの設計法 I 4. アナログフィルタを基にしたディジタル IIR フィルタの設計法 II 5. 双 次フィルタ LI 離散時間システムの基礎式の証明 [ ] 4. ] [ ]*
ディジタルフィルタの設計法. 逆フィルター. 直線位相 FIR フィルタの設計. 窓関数法による FIR フィルタの設計.5 時間領域での FIR フィルタの設計 3. アナログフィルタを基にしたディジタル IIR フィルタの設計法 I 4. アナログフィルタを基にしたディジタル IIR フィルタの設計法 II 5. 双 次フィルタ LI 離散時間システムの基礎式の証明 [ ] 4. ] [ ]*
代数 幾何 < ベクトル > 1 ベクトルの演算 和 差 実数倍については 文字の計算と同様 2 ベクトルの成分表示 平面ベクトル : a x e y e x, ) ( 1 y1 空間ベクトル : a x e y e z e x, y, ) ( 1 1 z1
 代数 幾何 < ベクトル > ベクトルの演算 和 差 実数倍については 文字の計算と同様 ベクトルの成分表示 平面ベクトル :, 空間ベクトル : z,, z 成分での計算ができるようにすること ベクトルの内積 : os 平面ベクトル :,, 空間ベクトル :,,,, z z zz 4 ベクトルの大きさ 平面上 : 空間上 : z は 良く用いられる 5 m: に分ける点 : m m 図形への応用
代数 幾何 < ベクトル > ベクトルの演算 和 差 実数倍については 文字の計算と同様 ベクトルの成分表示 平面ベクトル :, 空間ベクトル : z,, z 成分での計算ができるようにすること ベクトルの内積 : os 平面ベクトル :,, 空間ベクトル :,,,, z z zz 4 ベクトルの大きさ 平面上 : 空間上 : z は 良く用いられる 5 m: に分ける点 : m m 図形への応用
Microsoft Word - 補論3.2
 補論 3. 多変量 GARC モデル 07//6 新谷元嗣 藪友良 対数尤度関数 3 章 7 節では 変量の対数尤度を求めた ここでは多変量の場合 とくに 変量について対数尤度を求める 誤差項 は平均 0 で 次元の正規分布に従うとする 単純化のため 分散と共分散は時間を通じて一定としよう ( この仮定は後で変更される ) したがって ij から添え字 を除くことができる このとき と の尤度関数は
補論 3. 多変量 GARC モデル 07//6 新谷元嗣 藪友良 対数尤度関数 3 章 7 節では 変量の対数尤度を求めた ここでは多変量の場合 とくに 変量について対数尤度を求める 誤差項 は平均 0 で 次元の正規分布に従うとする 単純化のため 分散と共分散は時間を通じて一定としよう ( この仮定は後で変更される ) したがって ij から添え字 を除くことができる このとき と の尤度関数は
3 数値解の特性 3.1 CFL 条件 を 前の章では 波動方程式 f x= x0 = f x= x0 t f c x f =0 [1] c f 0 x= x 0 x 0 f x= x0 x 2 x 2 t [2] のように差分化して数値解を求めた ここでは このようにして得られた数値解の性質を 考
![3 数値解の特性 3.1 CFL 条件 を 前の章では 波動方程式 f x= x0 = f x= x0 t f c x f =0 [1] c f 0 x= x 0 x 0 f x= x0 x 2 x 2 t [2] のように差分化して数値解を求めた ここでは このようにして得られた数値解の性質を 考 3 数値解の特性 3.1 CFL 条件 を 前の章では 波動方程式 f x= x0 = f x= x0 t f c x f =0 [1] c f 0 x= x 0 x 0 f x= x0 x 2 x 2 t [2] のように差分化して数値解を求めた ここでは このようにして得られた数値解の性質を 考](/thumbs/103/158269281.jpg) 3 数値解の特性 3.1 CFL 条件 を 前の章では 波動方程式 f x= x = f x= x t f c x f = [1] c f x= x f x= x 2 2 t [2] のように差分化して数値解を求めた ここでは このようにして得られた数値解の性質を 考える まず 初期時刻 t=t に f =R f exp [ik x ] [3] のような波動を与えたとき どのように時間変化するか調べる
3 数値解の特性 3.1 CFL 条件 を 前の章では 波動方程式 f x= x = f x= x t f c x f = [1] c f x= x f x= x 2 2 t [2] のように差分化して数値解を求めた ここでは このようにして得られた数値解の性質を 考える まず 初期時刻 t=t に f =R f exp [ik x ] [3] のような波動を与えたとき どのように時間変化するか調べる
7 渦度方程式 総観規模あるいは全球規模の大気の運動を考える このような大きな空間スケールでの大気の運動においては 鉛直方向の運動よりも水平方向の運動のほうがずっと大きい しかも 水平方向の運動の中でも 収束 発散成分は相対的に小さく 低気圧や高気圧などで見られるような渦 つまり回転成分のほうが卓越
 7 渦度方程式 総観規模あるいは全球規模の大気の運動を考える このような大きな空間スケールでの大気の運動においては 鉛直方向の運動よりも水平方向の運動のほうがずっと大きい しかも 水平方向の運動の中でも 収束 発散成分は相対的に小さく 低気圧や高気圧などで見られるような渦 つまり回転成分のほうが卓越している そこで 回転成分に着目して大気の運動を論じる 7.1 渦度 大気の回転成分を定量化する方法を考えてみる
7 渦度方程式 総観規模あるいは全球規模の大気の運動を考える このような大きな空間スケールでの大気の運動においては 鉛直方向の運動よりも水平方向の運動のほうがずっと大きい しかも 水平方向の運動の中でも 収束 発散成分は相対的に小さく 低気圧や高気圧などで見られるような渦 つまり回転成分のほうが卓越している そこで 回転成分に着目して大気の運動を論じる 7.1 渦度 大気の回転成分を定量化する方法を考えてみる
1/10 平成 29 年 3 月 24 日午後 1 時 37 分第 5 章ローレンツ変換と回転 第 5 章ローレンツ変換と回転 Ⅰ. 回転 第 3 章光速度不変の原理とローレンツ変換 では 時間の遅れをローレンツ変換 ct 移動 v相対 v相対 ct - x x - ct = c, x c 2 移動
 / 平成 9 年 3 月 4 日午後 時 37 分第 5 章ローレンツ変換と回転 第 5 章ローレンツ変換と回転 Ⅰ. 回転 第 3 章光速度不変の原理とローレンツ変換 では 時間の遅れをローレンツ変換 t t - x x - t, x 静止静止静止静止 を導いた これを 図の場合に当てはめると t - x x - t t, x t + x x + t t, x (5.) (5.) (5.3) を得る
/ 平成 9 年 3 月 4 日午後 時 37 分第 5 章ローレンツ変換と回転 第 5 章ローレンツ変換と回転 Ⅰ. 回転 第 3 章光速度不変の原理とローレンツ変換 では 時間の遅れをローレンツ変換 t t - x x - t, x 静止静止静止静止 を導いた これを 図の場合に当てはめると t - x x - t t, x t + x x + t t, x (5.) (5.) (5.3) を得る
DVIOUT
 最適レギュレータ 松尾研究室資料 第 最適レギュレータ 節時不変型無限時間最適レギュレータ 状態フィードバックの可能な場合の無限時間問題における最適レギュレータについて確定系について説明する. ここで, レギュレータとは状態量をゼロにするようなコントローラのことである. なぜ, 無限時間問題のみを述べるかという理由は以下のとおりである. 有限時間の最適レギュレータ問題の場合の最適フィードバックゲインは微分方程式の解から構成される時間関数として表現される.
最適レギュレータ 松尾研究室資料 第 最適レギュレータ 節時不変型無限時間最適レギュレータ 状態フィードバックの可能な場合の無限時間問題における最適レギュレータについて確定系について説明する. ここで, レギュレータとは状態量をゼロにするようなコントローラのことである. なぜ, 無限時間問題のみを述べるかという理由は以下のとおりである. 有限時間の最適レギュレータ問題の場合の最適フィードバックゲインは微分方程式の解から構成される時間関数として表現される.
点におけるひずみの定義 ( その1)-(ε, ε,γ ) の定義ひずみは 構造物の中で変化しているのが一般的である このために 応力と同様に 構造物内の任意の点で定義できるようにした方がよい また 応力と同様に 一つの点に注目しても ひずみは向きによって値が異なる これらを勘案し あ
 3. 変位とひずみ 3.1 変位関数構造物は外力の作用の下で変形する いま この変形により構造物内の任意の点 P(,,z) が P (',',z') に移動したものとする ( 図 3.1 参照 ) (,,z) は変形前の点 Pの座標 (',', z') は変形後の座標である このとき 次式で示される変形前後の座標の差 u ='- u ='- u z =z'-z (3.1) を変位成分と呼ぶ 変位 (
3. 変位とひずみ 3.1 変位関数構造物は外力の作用の下で変形する いま この変形により構造物内の任意の点 P(,,z) が P (',',z') に移動したものとする ( 図 3.1 参照 ) (,,z) は変形前の点 Pの座標 (',', z') は変形後の座標である このとき 次式で示される変形前後の座標の差 u ='- u ='- u z =z'-z (3.1) を変位成分と呼ぶ 変位 (
Microsoft Word - 断面諸量
 応用力学 Ⅱ 講義資料 / 断面諸量 断面諸量 断面 次 次モーメントの定義 図 - に示すような形状を有する横断面を考え その全断面積を とする いま任意に定めた直交座標軸 O-, をとり また図中の斜線部の微小面積要素を d とするとき d, d () で定義される, をそれぞれ与えられた横断面の 軸, 軸に関する断面 次モーメント (geometrcal moment of area) という
応用力学 Ⅱ 講義資料 / 断面諸量 断面諸量 断面 次 次モーメントの定義 図 - に示すような形状を有する横断面を考え その全断面積を とする いま任意に定めた直交座標軸 O-, をとり また図中の斜線部の微小面積要素を d とするとき d, d () で定義される, をそれぞれ与えられた横断面の 軸, 軸に関する断面 次モーメント (geometrcal moment of area) という
Chap3.key
 区分求積法. 面積 ( )/ f () > n + n, S 長方形の和集合で近似 n f (n ) リーマン和 f (n ) 区分求積法 リーマン和 S S n n / n n f ()d リーマン積分 ( + ) + S (, f ( )) 微分の心 Zoom In して局所的な性質を調べる 積分の心 Zoom Ou して大域的な性質を調べる 曲線の長さ 領域の面積や体積 ある領域に含まれる物質の質量
区分求積法. 面積 ( )/ f () > n + n, S 長方形の和集合で近似 n f (n ) リーマン和 f (n ) 区分求積法 リーマン和 S S n n / n n f ()d リーマン積分 ( + ) + S (, f ( )) 微分の心 Zoom In して局所的な性質を調べる 積分の心 Zoom Ou して大域的な性質を調べる 曲線の長さ 領域の面積や体積 ある領域に含まれる物質の質量
数学の世界
 東京女子大学文理学部数学の世界 (2002 年度 ) 永島孝 17 6 行列式の基本法則と効率的な計算法 基本法則 三次以上の行列式についても, 二次の場合と同様な法則がなりたつ ここには三次の場合を例示するが, 四次以上でも同様である 1 単位行列の行列式の値は 1 である すなわち 1 0 0 0 1 0 1 0 0 1 2 二つの列を入れ替えると行列式の値は 1 倍になる 例えば a 13 a
東京女子大学文理学部数学の世界 (2002 年度 ) 永島孝 17 6 行列式の基本法則と効率的な計算法 基本法則 三次以上の行列式についても, 二次の場合と同様な法則がなりたつ ここには三次の場合を例示するが, 四次以上でも同様である 1 単位行列の行列式の値は 1 である すなわち 1 0 0 0 1 0 1 0 0 1 2 二つの列を入れ替えると行列式の値は 1 倍になる 例えば a 13 a
Microsoft PowerPoint - H22制御工学I-2回.ppt
 制御工学 I 第二回ラプラス変換 平成 年 4 月 9 日 /4/9 授業の予定 制御工学概論 ( 回 ) 制御技術は現在様々な工学分野において重要な基本技術となっている 工学における制御工学の位置づけと歴史について説明する さらに 制御システムの基本構成と種類を紹介する ラプラス変換 ( 回 ) 制御工学 特に古典制御ではラプラス変換が重要な役割を果たしている ラプラス変換と逆ラプラス変換の定義を紹介し
制御工学 I 第二回ラプラス変換 平成 年 4 月 9 日 /4/9 授業の予定 制御工学概論 ( 回 ) 制御技術は現在様々な工学分野において重要な基本技術となっている 工学における制御工学の位置づけと歴史について説明する さらに 制御システムの基本構成と種類を紹介する ラプラス変換 ( 回 ) 制御工学 特に古典制御ではラプラス変換が重要な役割を果たしている ラプラス変換と逆ラプラス変換の定義を紹介し
2018年度 神戸大・理系数学
 8 神戸大学 ( 理系 ) 前期日程問題 解答解説のページへ t を < t < を満たす実数とする OABC を 辺の長さが の正四面体とする 辺 OA を -t : tに内分する点を P, 辺 OB を t :-tに内分する点を Q, 辺 BC の中点を R とする また a = OA, b = OB, c = OC とする 以下の問いに答えよ () QP と QR をt, a, b, c を用いて表せ
8 神戸大学 ( 理系 ) 前期日程問題 解答解説のページへ t を < t < を満たす実数とする OABC を 辺の長さが の正四面体とする 辺 OA を -t : tに内分する点を P, 辺 OB を t :-tに内分する点を Q, 辺 BC の中点を R とする また a = OA, b = OB, c = OC とする 以下の問いに答えよ () QP と QR をt, a, b, c を用いて表せ
s ss s ss = ε = = s ss s (3) と表される s の要素における s s = κ = κ, =,, (4) jωε jω s は複素比誘電率に相当する物理量であり ここで PML 媒質定数を次のように定義する すなわち κξ をPML 媒質の等価比誘電率 ξ をPML 媒質の
 FDTD 解析法 (Matlab 版 2 次元 PML) プログラム解説 v2.11 1. 概要 FDTD 解析における吸収境界である完全整合層 (Perfectl Matched Laer, PML) の定式化とプログラミングを2 次元 TE 波について解説する PMLは異方性の損失をもつ仮想的な物質であり 侵入して来る電磁波を逃さず吸収する 通常の物質と接する界面でインピーダンスが整合しており
FDTD 解析法 (Matlab 版 2 次元 PML) プログラム解説 v2.11 1. 概要 FDTD 解析における吸収境界である完全整合層 (Perfectl Matched Laer, PML) の定式化とプログラミングを2 次元 TE 波について解説する PMLは異方性の損失をもつ仮想的な物質であり 侵入して来る電磁波を逃さず吸収する 通常の物質と接する界面でインピーダンスが整合しており
数学 ⅡB < 公理 > 公理を論拠に定義を用いて定理を証明する 1 大小関係の公理 順序 (a > b, a = b, a > b 1 つ成立 a > b, b > c a > c 成立 ) 順序と演算 (a > b a + c > b + c (a > b, c > 0 ac > bc) 2 図
 数学 Ⅱ < 公理 > 公理を論拠に定義を用いて定理を証明する 大小関係の公理 順序 >, =, > つ成立 >, > > 成立 順序と演算 > + > + >, > > 図形の公理 平行線の性質 錯角 同位角 三角形の合同条件 三角形の合同相似 量の公理 角の大きさ 線分の長さ < 空間における座漂とベクトル > ベクトルの演算 和 差 実数倍については 文字の計算と同様 ベクトルの成分表示 平面ベクトル
数学 Ⅱ < 公理 > 公理を論拠に定義を用いて定理を証明する 大小関係の公理 順序 >, =, > つ成立 >, > > 成立 順序と演算 > + > + >, > > 図形の公理 平行線の性質 錯角 同位角 三角形の合同条件 三角形の合同相似 量の公理 角の大きさ 線分の長さ < 空間における座漂とベクトル > ベクトルの演算 和 差 実数倍については 文字の計算と同様 ベクトルの成分表示 平面ベクトル
ファイナンスのための数学基礎 第1回 オリエンテーション、ベクトル
 時系列分析 変量時系列モデルとその性質 担当 : 長倉大輔 ( ながくらだいすけ 時系列モデル 時系列モデルとは時系列データを生み出すメカニズムとなるものである これは実際には未知である 私たちにできるのは観測された時系列データからその背後にある時系列モデルを推測 推定するだけである 以下ではいくつかの代表的な時系列モデルを考察する 自己回帰モデル (Auoregressive Model もっとも頻繁に使われる時系列モデルは自己回帰モデル
時系列分析 変量時系列モデルとその性質 担当 : 長倉大輔 ( ながくらだいすけ 時系列モデル 時系列モデルとは時系列データを生み出すメカニズムとなるものである これは実際には未知である 私たちにできるのは観測された時系列データからその背後にある時系列モデルを推測 推定するだけである 以下ではいくつかの代表的な時系列モデルを考察する 自己回帰モデル (Auoregressive Model もっとも頻繁に使われる時系列モデルは自己回帰モデル
Probit , Mixed logit
 Probit, Mixed logit 2016/5/16 スタートアップゼミ #5 B4 後藤祥孝 1 0. 目次 Probit モデルについて 1. モデル概要 2. 定式化と理解 3. 推定 Mixed logit モデルについて 4. モデル概要 5. 定式化と理解 6. 推定 2 1.Probit 概要 プロビットモデルとは. 効用関数の誤差項に多変量正規分布を仮定したもの. 誤差項には様々な要因が存在するため,
Probit, Mixed logit 2016/5/16 スタートアップゼミ #5 B4 後藤祥孝 1 0. 目次 Probit モデルについて 1. モデル概要 2. 定式化と理解 3. 推定 Mixed logit モデルについて 4. モデル概要 5. 定式化と理解 6. 推定 2 1.Probit 概要 プロビットモデルとは. 効用関数の誤差項に多変量正規分布を仮定したもの. 誤差項には様々な要因が存在するため,
Taro-F25理論 印刷原稿
 第 種理論 A 問題 ( 配点は 問題当たり小問各 点, 計 0 点 ) 問 次の文章は, 真空中の静電界に関する諸法則の微分形に関する記述である 文中の に当てはまるものを解答群の中から選びなさい 図のように, 直交座標系において電界の z 軸成分が零となるような電界について, y 平面の二次元で電位や電界を考える ここで,4 点 (h,0),(0,h), (- h,0),(0,-h) の電位がそれぞれ
第 種理論 A 問題 ( 配点は 問題当たり小問各 点, 計 0 点 ) 問 次の文章は, 真空中の静電界に関する諸法則の微分形に関する記述である 文中の に当てはまるものを解答群の中から選びなさい 図のように, 直交座標系において電界の z 軸成分が零となるような電界について, y 平面の二次元で電位や電界を考える ここで,4 点 (h,0),(0,h), (- h,0),(0,-h) の電位がそれぞれ
