Microsoft PowerPoint - FEMintro [互換モード]
|
|
|
- あつみね おうじ
- 5 years ago
- Views:
Transcription
1 有限要素法入門 年夏季集中講義中島研吾 並列計算プログラミング 先端計算機演習 66-49
2 EM-ntro 有限要素法入門 偏微分方程式の数値解法 重み付き残差法 ガウス グリーンの定理 偏微分方程式の数値解法 変分法
3 EM-ntro 差分法と有限要素法 偏微分方程式の近似解法 全領域を小領域 メッシュ 要素 に分割する 差分法 微分係数を直接近似 Tylor 展開
4 EM-ntro 差分法 念のため 差分について 4 差分法 :nte fference Method マクロな微分 微分係数を数値的に近似する手法 以下のような一次元系を考える - +
5 直感的な定義 と + の中点 における微分係数 - + d d / となると微分係数の定義そのもの における二階微分係数 / / d d d d d d 差分法 5 EM-ntro
6 厳密な定義 :Tylor 展開 / - +!!!! 差分法 6 EM-ntro
7 厳密な定義 :Tylor 展開 / - +!!!! 前進差分!! 打ち切り誤差が のオーダー 一次精度!! 後退差分打ち切り誤差が のオーダー 一次精度 差分法 7 EM-ntro
8 厳密な定義 :Tylor 展開 / - +!!!! 中央差分 中心差分! 打ち切り誤差が のオーダー 二次精度 差分法 8 EM-ntro
9 直感的な定義 : 実は二次精度 - + / / / /! /! / / / /! / 打ち切り誤差が のオーダー 二次精度 / / / /! /! / / 二点間の中点で二次精度 それ以外の点では一次精度 ということもできる が均一でない場合も同様のことが起こる 差分法 9 EM-ntro
10 Intro- 一次元熱伝導方程式 / 要素単位の線形方程式 各要素における線形方程式は以下のような形になる / / d d d d d d 差分法による離散化 A A A N A A A R L R L d d N N 差分法 EM-ntro
11 EM-ntro 差分法と有限要素法 偏微分方程式の近似解法 全領域を小領域 メッシュ 要素 に分割する 差分法 微分係数を直接近似 Tylor 展開 有限要素法 nte Element MethodEM 積分形式で定式化された 弱形式 ek form を解く 微分方程式の解 古典解 に対して 弱解 ek solton 重み付き残差法 変分法 複雑形状への適用 差分でもある程度の複雑形状は扱うことが可能
12 EM-ntro 差分法で複雑形状を扱う例 Hndbook of Grd Generton 座標変換
13 EM-ntro 分でわかる有限要素法 nte-element Method EM 偏微分方程式の解法として広く知られている elements meshes 要素 & nodes vertces 節点 以下の二次元熱伝導問題を考える : T T y Q 6 節点 9 要素 四角形 一様な熱伝導率 = 一様な体積発熱 Q= 節点 で温度固定 :T= 周囲断熱
14 EM-ntro 分でわかる有限要素法 4 Glerkn EM procedres 各要素にガラーキン法を適用 : V T T y N T Q dv 各要素で : T } N { [N] : 形状関数 内挿関数 偏微分方程式に対して ガウス グリーンの定理を適用し 以下の 弱形式 を導く V V T T N N N N T dv Q N y y dv
15 Element Mtr: 要素マトリクス 各要素において積分を実行し 要素マトリクスを得る e C A } { } ]{ [ e e C e e A e e C e e A e e C e e A e C e CC e C e CA e e C e e A e A e AC e A e AA e e e f f f f k k k k k k k k k k k k k k k k f k dv Q N dv y N y N N N V T T T V 分でわかる有限要素法 5 EM-ntro
16 Globl/overll Mtr: 全体マトリクス各要素マトリクスを全体マトリクスに足しこむ } { } ]{ [ K 分でわかる有限要素法 6 EM-ntro
17 Globl/overll Mtr: 全体マトリクス各要素マトリクスを全体マトリクスに足しこむ } { } ]{ [ K 分でわかる有限要素法 7 EM-ntro
18 得られた大規模連立一次方程式を解くある適切な境界条件 ここでは = を適用 疎 ゼロが多い な行列 分でわかる有限要素法 8 EM-ntro
19 EM-ntro 分でわかる有限要素法 9 計算結果 T T y Q
20 EM-ntro 有限要素法の利点 要素内でのローカルな処理が中心となっている 特に高次要素 混合補間要素の定式化が容易 非圧縮性流体の場合 有限要素法 : 速度 圧力 : 速度差分法 : スタガード格子圧力用のメッシュ
21 EM-ntro 有限要素法の利点 要素内でのローカルな処理が中心となっている 特に高次要素 混合補間要素の定式化が容易 非圧縮性流体の場合 有限要素法 : 速度 圧力 : 速度差分法 : スタガード格子 方向速度用のメッシュ
22 EM-ntro 有限要素法の利点 要素内でのローカルな処理が中心となっている 特に高次要素 混合補間要素の定式化が容易 非圧縮性流体の場合 有限要素法 : 速度 圧力 : 速度差分法 : スタガード格子 Y 方向速度用のメッシュ
23 EM-ntro 有限要素法の歴史 航空機の構造計算の手法として 95 年代前半 ボーイング社 ワシントン大学 Unversty of Wshngton の研究者ら M.J.Trner H.C.Mrtn によって提案 後退翼 : 梁理論では対応できない 様々な分野への拡張 非線形 :T.J.Oden 構造力学以外の分野 :O.C.Zenkecz 商用パッケージ NASTRAN NASAによって開発された有限要素法による構造解析プログラム 米国 MSC 社によって商用化 製造業において広く使用されている PC 化により爆発的に普及
24 EM-ntro 4 代表的な商用パッケージ MSC/NASTRAN ANSYS 工学系の学科では これらの商用コードを授業に導入し それを使って弾性力学そのものを教えたりするような例もある
25 EM-ntro 5 非線形分野への応用 破壊 衝突 接触 材料非線形 並列計算 最近のトピックス 商用コードにおいても並列版が登場しつつある 適応格子 :Adptve Mesh Refnement 衝撃波 剥離 応力集中 並列計算時 : 動的負荷分散 格子生成 特に大規模並列メッシュ生成
26 EM-ntro 6 球周囲の超音速流れ マッハ数 =.4 理想気体 一様流れ レイノルズ数 Re= 6 Intl Grd 負荷分散 前後 PE 7 - PE 7 - PE 6 - PE 6 - -Lev. Adpted 負荷分散 前後 Lev. Adpted 負荷分散 前後
27 EM-ntro 7 三次元地殻変動シミュレーションへの 適用例 move
28 EM-ntro 8 参考文献 / 菊地 有限要素法概説 新訂版 サイエンス社 999. 竹内 樫山 寺田 日本計算工学会編 計算力学 : 有限要素法の基礎 森北出版. 登坂 大西 偏微分方程式の数値シミュレーション第 版 東大出版会. 差分法 境界要素法との比較 福森 よくわかる有限要素法 オーム社 5. ヘルムホルツ方程式 矢川 宮崎 有限要素法による熱応力 クリープ 熱伝導解析 サイエンス社 985. 品切 Segerlnd L. 川井監訳 応用有限要素解析第 版 丸善 99. 品切
29 EM-ntro 9 参考文献 / sh elytschko 山田 永井 松井訳 有限要素法 丸善 8. 原著 A rst Corse n nte Elements AAQUS Stdent Edton が附属
30 EM-ntro 参考文献 より進んだ読者向け 菊池 岡部 有限要素システム入門 日科技連 986. 山田 高性能有限要素法 丸善 7. 奥田 中島 並列有限要素法 培風館 4. Smth I. 他 Progrmmng the nte Element Method 4th edton Wley.
31 EM-ntro 有限要素法入門 偏微分方程式の数値解法 重み付き残差法 ガウス グリーンの定理 偏微分方程式の数値解法 変分法
32 EM-ntro 偏微分方程式の近似解法 領域 V 境界 S における以下の微分方程式を解くことを考える 境界値問題 : L f 微分方程式の解 が以下のような関数 M で近似的に表されるものとする 一次結合 線形結合 : M M 領域 境界において定義される 位置座標のみ既知関数 互いに独立である : 試行関数 trl/test fncton と呼ばれる 線形代数における基底 bss に相当する 係数 未知数
33 EM-ntro 重み付き残差法 Method of Weghted Resdl MWR 以下に示す残差 resdlr が であれば厳密解である : R L M f 重み付き残差法では残差 R に重み関数 eght/eghtng fncton を乗じて 領域全体で積分した量が になるような条件を考える : V R M dv 重み付き残差法は 残差 = の条件を領域において 平均的に 満たす近似解法である
34 EM-ntro 4 変分法 Rtz 法 / 多くの問題においては汎関数 fnctonli が存在し 厳密解 が I を極値にすること 停留 が知られている 汎関数が極値を持つためにが満たすべき微分方程式をオイラー Eler 方程式という 逆に Eler 方程式を満たすためには が I を停留させていれば良い 例えば 弾性力学の支配方程式 平衡方程式 仮想仕事の原理 と等価な汎関数は 最小ポテンシャルエネルギの原理 ひずみエネルギ最小の法則 である
35 EM-ntro 5 変分法 Rtz 法 / 以下の近似解の式をI に代入し I M = I M が極値になるようにすれば 係数 が求められ M が決定される M M 変分法は偏微分方程式の近似解法としては 理論的 数学的 物理的な背景が堅牢で理解しやすいのであるが 等価な変分問題を持つような微分方程式で無いと適用できない : 本授業では重み付き残差法を使用する 厳密解 解析解に近いものと考えられる
36 EM-ntro 6 有限要素法 全体を細かい要素に分割し 各要素に対して以下の近似を適用する : M M 各要素に対して 重み付き残差法 または変分法 後述 を適用する 全体の効果を足し合わせて 結果的に得られる連立一次方程式を解くことによって 偏微分方程式の近似解を求める 分で分かる有限要素法
37 EM-ntro 7 重み付き残差法の例 / 熱伝導方程式 Q y T T T t 境界 S n 領域 V S V 近似解 j n j j T : 熱伝導率 領域 V で一様 Q: 体積あたり発熱量 残差 Q y y R j j n j j j
38 EM-ntro 8 重み付き残差法の例 / 重み関数 を乗じて積分 dv R V 重み関数 が n 個の異なる関数であるとすれば 上式は n 個の連立一次方程式となる 試行関数の数 = 重み関数の数... n Q dv dv y n j V j j V j
39 EM-ntro 9 重み付き残差法の例 / 行列の形式で書くと以下のようになる Q Q dv Q dv y V j j V j 実際はこれとは少しちがう
40 EM-ntro 4 様々な重み付き残差法 重み関数の定義の仕方が異なる 選点法 Collocton Method 最小二乗法 Lest Sqre Method ガラーキン法 Glerkn Method
41 EM-ntro 4 選点法 Collocton Method ディラックのデルタ関数を重み関数として選ぶ 引数 =のとき無限大 それ以外ではの値をとる 積分すると = : 座標ベクトル デルタ関数の性質を利用して n 個の選点 collocton pont で残差 R が になるように定め n を増加させることによって領域全体で残差 = となる dv R R V
42 EM-ntro 4 最小二乗法 Lest Sqre Method 重み関数として 以下を与える : R 以下の積分を未知数 について最小化する : dv R I V dv R R I V dv R R V
43 EM-ntro 4 ガラーキン法 Glerkn Method 重み関数 = 試行関数 Glerkn ors Grgorevch ロシア 旧ソビエト連邦の工学者 数学者にして技術者 96 年 ~97 年に反帝政派として投獄中にガラーキン法のアイディアを考えついたらしい
44 EM-ntro 44 例題 / 支配方程式 d 固定境界条件 第一種境界条件 rchlet 型境界条件とも呼ぶ 従属変数の微分係数が境界条件として与えられる場合を第二種または Nemnn 型境界条件と呼ぶ 厳密解 確かめてみよ sn sn
45 EM-ntro 45 厳密解 sn sn
46 EM-ntro 46 例題 / 近似解を以下のように仮定する : 試行関数 : =@= を満たす 残差は以下のように表される : R 6 この問題に重みつき残差法の各手法を適用してみよう 未知数 試行関数 は の つなので 独立な 重み関数も つになる
47 EM-ntro 47 選点法 Collocton Method n= であるので =/4=/ を選点とすると : R R 4 R 6 したがって : 9 /6 7 / 4 5 / 64 7 / 8 / /
48 EM-ntro 48 最小二乗法 Lest Sqre Method 定義により : したがって : R R 6 d R d R R d R d R R R
49 EM-ntro 49 ガラーキン法 Glerkn Method 定義により : したがって : / / /5 / / / d R d R d R d R R
50 EM-ntro 5 計算結果の比較 厳密解選点法最小二乗法ガラーキン法 ガラーキン法が最も精度がよい 汎関数がある問題については 変分法とガラーキン法は答えが一致する 菊地 岡部 矢川 宮崎 一種の解析解 多くの商用コードでガラーキン法を使用 本授業でも今後ガラーキン法を扱う 高レイノルズ数 Nver-Stokes 方程式など 最小二乗法を適用して安定化する場合もある
51 EM-ntro 5 有限要素法入門 偏微分方程式の数値解法 重み付き残差法 ガウス グリーンの定理 偏微分方程式の数値解法 変分法
52 EM-ntro 5 ガウスの定理 :Gss s Theorem V U V y W z dv S Un Vn y Wn z ds 三次元デカルト座標 yz 滑らかな閉曲面 Sによって囲まれたV V 内で定義される つの連続関数 UyzVyzWyz 曲面 S 上で外向きに引いた法線ベクトル n n n y n z : 方向余弦 n V S
53 EM-ntro 5 ガウスの定理 :Gss s Theorem 簡単な証明 / 軸に平行な微小角柱を考えると : V U dv dy dz U d U y z dy dz U y z dy dz z y n V S V
54 EM-ntro 54 ガウスの定理 :Gss s Theorem 簡単な証明 / 角柱が表面 S から切り取る面積を ds とすると : dy dz n dy dz n ds ds したがって : V U S U dv U n ds dy y z dy S f f dz dz U n n n ds U d U y z dy dz V ds n n n n y z n
55 EM-ntro 55 ガウスの定理 :Gss s Theorem 簡単な証明 / これを全領域に拡張すると : U dv Un V S ds V 更に yz 方向に拡張して以下が成立 : ds V U V y W z dv S Un Vn y Wn z ds n n n n y z n
56 EM-ntro 56 グリーンの定理 / z A W y A V A U 以下のように仮定すると : 以下が導かれる : z z A y y A A z y A z W y V U これを積分してガウスの定理を適用すると以下が得られる : ds n z n y n A ds Wn Vn Un dv z z A y y A A dv z y A S z y S z y V V
57 EM-ntro 57 グリーンの定理 / 続き 結果として以下のようになる V V S dv z z A y y A A ds n A dv z y A ds n A ds n z z n y y n A ds n z n y n A S S S z y n 来週以降 よく登場します 二階微分の一階微分への置き換え : の法線方向勾配
58 EM-ntro 58 ベクトル表記すると ガウスの定理 V dv S T n ds グリーンの定理 v dv T T v n ds v dv V S V
59 EM-ntro 59 有限要素法入門 偏微分方程式の数値解法 重み付き残差法 ガウス グリーンの定理 偏微分方程式の数値解法 変分法
60 EM-ntro 6 再出 変分法 Rtz 法 / 多くの問題においては汎関数 fnctonli が存在し 厳密解 が I を極値にすること 停留 が知られている 汎関数が極値を持つためにが満たすべき微分方程式をオイラー Eler 方程式という 逆に Eler 方程式を満たすためには が I を停留させていれば良い 例えば 弾性力学の支配方程式 平衡方程式 仮想仕事の原理 と等価な汎関数は 最小ポテンシャルエネルギの原理 ひずみエネルギ最小の法則 である
61 EM-ntro 6 再出 変分法 Rtz 法 / 以下の近似解の式をI に代入し I M = I M が極値になるようにすれば 係数 が求められ M が決定される M M 変分法は偏微分方程式の近似解法としては 理論的 数学的 物理的な背景が堅牢で理解しやすいのであるが 等価な変分問題を持つような微分方程式で無いと適用できない : 本授業では重み付き残差法を使用する
62 EM-ntro 6 汎関数 変分法による近似解例 /4 d I d 汎関数 I を上記の境界条件のもとに停留させる を求めよ 対応するオイラー方程式は以下である 重み付き残差法と同じ : d - d
63 EM-ntro 6 変分法による近似解例 /4 回連続微分可能な関数 に対して n 次の試行関数を以下のように仮定する : n n 試行関数の次数 n を増加させることにより n は真の解 に近づくことから 汎関数 I も I n によって近似可能である I n が停留すれば I も停留する 未知係数 k に対して 以下の停留条件を満たす k を求めれば良い : I n k ~ k n n - -
64 EM-ntro 64 リッツ Rtz 法 式 - は ~ n を未知数とする連立一次方程式となる この解を式 - に代入することにより I n を停留させる解 すなわちオイラー方程式 - を満たす解の近似解 が得られる 近似解ではあるが オイラー方程式を厳密に満たす このように 関数 を有限個の試行関数の列に展開し その際に導入される未知定数によって汎関数を停留する解を求める方法をリッツ Rtz 法と呼ぶ
65 EM-ntro 65 変分法による近似解例 /4 リッツ法適用 n= I d d d I d d d
66 /4 の補足 / リッツ法適用 n= d d d I d d
67 /4 の補足 / d d d d d I
68 /4 の補足 / 4 d d d d d I
69 EM-ntro 69 変分法による近似解例 4/4 これを整理すると以下のようになる : / / / /5 / / この結果はガラーキン法と一致する 決して偶然ではない
70 EM-ntro 7 ガラーキン法 Glerkn Method 定義により : したがって : / / /5 / / / d R d R d R d R R 試行関数 : =@= を満たす
71 EM-ntro 7 リッツ法とガラーキン法 /4 I I d d d d d d d d d d d d d d d I d d d d d d d d d d d d d d d d
72 EM-ntro 7 リッツ法とガラーキン法 /4 I d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d d
73 EM-ntro 7 リッツ法とガラーキン法 /4 I d d d d d d d d I d d d d d d d d ガラーキン法そのもの d d
74 EM-ntro 74 リッツ法とガラーキン法 4/4 今回示したのは非常に特殊な例ではあるが 一般的に汎関数が存在する場合 ガラーキン法とリッツ法は一致する リッツ法は近似解ではあるが オイラー方程式を厳密に満たしているので 厳密解 により近いと言える ガラーキン法の 精度 が高い理由 この事実だけをとりあえず覚えておいてください 汎関数が存在しない場合は成立しない 精度 安定性等の観点からガラーキン法が最良でない場合もある
有限要素法入門 中島研吾 東京大学情報基盤センター
 有限要素法入門 中島研吾 東京大学情報基盤センター EM-ntro 有限要素法入門 偏微分方程式の数値解法 重み付き残差法 偏微分方程式の数値解法 変分法 EM-ntro 差分法と有限要素法 偏微分方程式の近似解法 全領域を小領域 メッシュ 要素 に分割する 差分法 微分係数を直接近似 Tylor 展開 nte fference Method M Tylor Seres Epnson -!!!! nd
有限要素法入門 中島研吾 東京大学情報基盤センター EM-ntro 有限要素法入門 偏微分方程式の数値解法 重み付き残差法 偏微分方程式の数値解法 変分法 EM-ntro 差分法と有限要素法 偏微分方程式の近似解法 全領域を小領域 メッシュ 要素 に分割する 差分法 微分係数を直接近似 Tylor 展開 nte fference Method M Tylor Seres Epnson -!!!! nd
FEM原理講座 (サンプルテキスト)
 サンプルテキスト FEM 原理講座 サイバネットシステム株式会社 8 年 月 9 日作成 サンプルテキストについて 各講師が 講義の内容が伝わりやすいページ を選びました テキストのページは必ずしも連続していません 一部を抜粋しています 幾何光学講座については 実物のテキストではなくガイダンスを掲載いたします 対象とする構造系 物理モデル 連続体 固体 弾性体 / 弾塑性体 / 粘弾性体 / 固体
サンプルテキスト FEM 原理講座 サイバネットシステム株式会社 8 年 月 9 日作成 サンプルテキストについて 各講師が 講義の内容が伝わりやすいページ を選びました テキストのページは必ずしも連続していません 一部を抜粋しています 幾何光学講座については 実物のテキストではなくガイダンスを掲載いたします 対象とする構造系 物理モデル 連続体 固体 弾性体 / 弾塑性体 / 粘弾性体 / 固体
(Microsoft PowerPoint - \221\34613\211\361)
 計算力学 ~ 第 回弾性問題の有限要素解析 (Ⅱ)~ 修士 年後期 ( 選択科目 ) 担当 : 岩佐貴史 講義の概要 全 5 講義. 計算力学概論, ガイダンス. 自然現象の数理モデル化. 行列 場とその演算. 数値計算法 (Ⅰ) 5. 数値計算法 (Ⅱ) 6. 初期値 境界値問題 (Ⅰ) 7. 初期値 境界値問題 (Ⅱ) 8. マトリックス変位法による構造解析 9. トラス構造の有限要素解析. 重み付き残差法と古典的近似解法.
計算力学 ~ 第 回弾性問題の有限要素解析 (Ⅱ)~ 修士 年後期 ( 選択科目 ) 担当 : 岩佐貴史 講義の概要 全 5 講義. 計算力学概論, ガイダンス. 自然現象の数理モデル化. 行列 場とその演算. 数値計算法 (Ⅰ) 5. 数値計算法 (Ⅱ) 6. 初期値 境界値問題 (Ⅰ) 7. 初期値 境界値問題 (Ⅱ) 8. マトリックス変位法による構造解析 9. トラス構造の有限要素解析. 重み付き残差法と古典的近似解法.
パソコンシミュレータの現状
 第 2 章微分 偏微分, 写像 豊橋技術科学大学森謙一郎 2. 連続関数と微分 工学において物理現象を支配する方程式は微分方程式で表されていることが多く, 有限要素法も微分方程式を解く数値解析法であり, 定式化においては微分 積分が一般的に用いられており. 数学の基礎知識が必要になる. 図 2. に示すように, 微分は連続な関数 f() の傾きを求めることであり, 微小な に対して傾きを表し, を無限に
第 2 章微分 偏微分, 写像 豊橋技術科学大学森謙一郎 2. 連続関数と微分 工学において物理現象を支配する方程式は微分方程式で表されていることが多く, 有限要素法も微分方程式を解く数値解析法であり, 定式化においては微分 積分が一般的に用いられており. 数学の基礎知識が必要になる. 図 2. に示すように, 微分は連続な関数 f() の傾きを求めることであり, 微小な に対して傾きを表し, を無限に
Microsoft PowerPoint - シミュレーション工学-2010-第1回.ppt
 シミュレーション工学 ( 後半 ) 東京大学人工物工学研究センター 鈴木克幸 CA( Compter Aded geerg ) r. Jaso Lemo (SC, 98) 設計者が解析ツールを使いこなすことにより 設計の評価 設計の質の向上を図る geerg の本質の 計算機による支援 (CA CAM などより広い名前 ) 様々な汎用ソフトの登場 工業製品の設計に不可欠のツール 構造解析 流体解析
シミュレーション工学 ( 後半 ) 東京大学人工物工学研究センター 鈴木克幸 CA( Compter Aded geerg ) r. Jaso Lemo (SC, 98) 設計者が解析ツールを使いこなすことにより 設計の評価 設計の質の向上を図る geerg の本質の 計算機による支援 (CA CAM などより広い名前 ) 様々な汎用ソフトの登場 工業製品の設計に不可欠のツール 構造解析 流体解析
Microsoft PowerPoint - H21生物計算化学2.ppt
 演算子の行列表現 > L いま 次元ベクトル空間の基底をケットと書くことにする この基底は完全系を成すとすると 空間内の任意のケットベクトルは > > > これより 一度基底を与えてしまえば 任意のベクトルはその基底についての成分で完全に記述することができる これらの成分を列行列の形に書くと M これをベクトル の基底 { >} による行列表現という ところで 行列 A の共役 dont 行列は A
演算子の行列表現 > L いま 次元ベクトル空間の基底をケットと書くことにする この基底は完全系を成すとすると 空間内の任意のケットベクトルは > > > これより 一度基底を与えてしまえば 任意のベクトルはその基底についての成分で完全に記述することができる これらの成分を列行列の形に書くと M これをベクトル の基底 { >} による行列表現という ところで 行列 A の共役 dont 行列は A
Microsoft PowerPoint - 夏の学校(CFD).pptx
 /9/5 FD( 計算流体力学 ) の基礎理論 性能 運動分野 夏の学校 神戸大学大学院海事科学研究科勝井辰博 流体の質量保存 流体要素内の質量の増加率 [ 単位時間当たりの増加量 ] 単位時間に流体要素に流入する質量 流体要素 Fl lm (orol olm) v ( ) ガウスの定理 v( ) /9/5 = =( ) b=b =(b b b ) b= b = b + b + b アインシュタイン表記
/9/5 FD( 計算流体力学 ) の基礎理論 性能 運動分野 夏の学校 神戸大学大学院海事科学研究科勝井辰博 流体の質量保存 流体要素内の質量の増加率 [ 単位時間当たりの増加量 ] 単位時間に流体要素に流入する質量 流体要素 Fl lm (orol olm) v ( ) ガウスの定理 v( ) /9/5 = =( ) b=b =(b b b ) b= b = b + b + b アインシュタイン表記
静的弾性問題の有限要素法解析アルゴリズム
 概要 基礎理論. 応力とひずみおよび平衡方程式. 降伏条件式. 構成式 ( 応力 - ひずみ関係式 ) 有限要素法. 有限要素法の概要. 仮想仕事の原理式と変分原理. 平面ひずみ弾性有限要素法定式化 FEM の基礎方程式平衡方程式. G G G ひずみ - 変位関係式 w w w. kl jkl j D 構成式応力 - ひずみ関係式 ) (. 変位の境界条件力の境界条件境界条件式 t S on V
概要 基礎理論. 応力とひずみおよび平衡方程式. 降伏条件式. 構成式 ( 応力 - ひずみ関係式 ) 有限要素法. 有限要素法の概要. 仮想仕事の原理式と変分原理. 平面ひずみ弾性有限要素法定式化 FEM の基礎方程式平衡方程式. G G G ひずみ - 変位関係式 w w w. kl jkl j D 構成式応力 - ひずみ関係式 ) (. 変位の境界条件力の境界条件境界条件式 t S on V
<4D F736F F F696E74202D20906C8D488AC28BAB90DD8C7689F090CD8D488A D91E F1>
 人工環境設計解析工学構造力学と有限要素法 ( 第 回 ) 東京大学新領域創成科学研究科 鈴木克幸 固体力学の基礎方程式 変位 - ひずみの関係 適合条件式 ひずみ - 応力の関係 構成方程式 応力 - 外力の関係 平衡方程式 境界条件 変位規定境界 反力規定境界 境界条件 荷重応力ひずみ変形 場の方程式 Γ t Γ t 平衡方程式構成方程式適合条件式 構造力学の基礎式 ひずみ 一軸 荷重応力ひずみ変形
人工環境設計解析工学構造力学と有限要素法 ( 第 回 ) 東京大学新領域創成科学研究科 鈴木克幸 固体力学の基礎方程式 変位 - ひずみの関係 適合条件式 ひずみ - 応力の関係 構成方程式 応力 - 外力の関係 平衡方程式 境界条件 変位規定境界 反力規定境界 境界条件 荷重応力ひずみ変形 場の方程式 Γ t Γ t 平衡方程式構成方程式適合条件式 構造力学の基礎式 ひずみ 一軸 荷重応力ひずみ変形
JSMECM教育認定
 一般社団法人日本機械学会 018/09/6 計算力学技術者 級問題集 ( 固体力学分野 )018 年度版 ( 第 9 版 3 刷 ) P 項目誤正 175 問 -6/ 上 8 行 1 1 sin cos sin cos rs y y xy rs y x xy i 計算力学技術者 級 ( 固体力学分野の有限要素法解析技術者 ) の認定の範囲 認定技術者の技術レベル本認定を取得した技術者は, 基本的な固体力学の問題に対して,
一般社団法人日本機械学会 018/09/6 計算力学技術者 級問題集 ( 固体力学分野 )018 年度版 ( 第 9 版 3 刷 ) P 項目誤正 175 問 -6/ 上 8 行 1 1 sin cos sin cos rs y y xy rs y x xy i 計算力学技術者 級 ( 固体力学分野の有限要素法解析技術者 ) の認定の範囲 認定技術者の技術レベル本認定を取得した技術者は, 基本的な固体力学の問題に対して,
Microsoft Word - NumericalComputation.docx
 数値計算入門 武尾英哉. 離散数学と数値計算 数学的解法の中には理論計算では求められないものもある. 例えば, 定積分は, まずは積分 ( 被積分関数の原始関数をみつけること できなければ値を得ることはできない. また, ある関数の所定の値における微分値を得るには, まずその関数の微分ができなければならない. さらに代数方程式の解を得るためには, 解析的に代数方程式を解く必要がある. ところが, これらは必ずしも解析的に導けるとは限らない.
数値計算入門 武尾英哉. 離散数学と数値計算 数学的解法の中には理論計算では求められないものもある. 例えば, 定積分は, まずは積分 ( 被積分関数の原始関数をみつけること できなければ値を得ることはできない. また, ある関数の所定の値における微分値を得るには, まずその関数の微分ができなければならない. さらに代数方程式の解を得るためには, 解析的に代数方程式を解く必要がある. ところが, これらは必ずしも解析的に導けるとは限らない.
数学の世界
 東京女子大学文理学部数学の世界 (2002 年度 ) 永島孝 17 6 行列式の基本法則と効率的な計算法 基本法則 三次以上の行列式についても, 二次の場合と同様な法則がなりたつ ここには三次の場合を例示するが, 四次以上でも同様である 1 単位行列の行列式の値は 1 である すなわち 1 0 0 0 1 0 1 0 0 1 2 二つの列を入れ替えると行列式の値は 1 倍になる 例えば a 13 a
東京女子大学文理学部数学の世界 (2002 年度 ) 永島孝 17 6 行列式の基本法則と効率的な計算法 基本法則 三次以上の行列式についても, 二次の場合と同様な法則がなりたつ ここには三次の場合を例示するが, 四次以上でも同様である 1 単位行列の行列式の値は 1 である すなわち 1 0 0 0 1 0 1 0 0 1 2 二つの列を入れ替えると行列式の値は 1 倍になる 例えば a 13 a
2014 年 10 月 2 日 本日の講義及び演習 数値シミュレーション 2014 年度第 2 回 偏微分方程式の偏微分項をコンピュータで扱えるようにする 離散化 ( 差分化 ) テイラー展開の利用 1 階微分項に対する差分式 2 階微分項に対する差分式 1 次元熱伝導方程式に適用して差分式を導出
 04 年 0 月 日 本日の講義及び演習 数値シミュレーション 04 年度第 回 偏微分方程式の偏微分項をコンピュータで扱えるようにする 離散化 ( 差分化 テイラー展開の利用 階微分項に対する差分式 階微分項に対する差分式 次元熱伝導方程式に適用して差分式を導出 Ecel を利用した温度変化シミュレーション 永野 ( 熱流体システム研究室 hagao@tc.ac.p 重要! 熱の伝わり方 ( 伝熱モード
04 年 0 月 日 本日の講義及び演習 数値シミュレーション 04 年度第 回 偏微分方程式の偏微分項をコンピュータで扱えるようにする 離散化 ( 差分化 テイラー展開の利用 階微分項に対する差分式 階微分項に対する差分式 次元熱伝導方程式に適用して差分式を導出 Ecel を利用した温度変化シミュレーション 永野 ( 熱流体システム研究室 hagao@tc.ac.p 重要! 熱の伝わり方 ( 伝熱モード
OpenFOAM(R) ソースコード入門 pt1 熱伝導方程式の解法から有限体積法の実装について考える 前編 : 有限体積法の基礎確認 2013/11/17 オープンCAE 富山富山県立大学中川慎二
 OpenFOAM(R) ソースコード入門 pt1 熱伝導方程式の解法から有限体積法の実装について考える 前編 : 有限体積法の基礎確認 2013/11/17 オープンCAE 勉強会 @ 富山富山県立大学中川慎二 * OpenFOAM のソースコードでは, 基礎式を偏微分方程式の形で記述する.OpenFOAM 内部では, 有限体積法を使ってこの微分方程式を解いている. どのようにして, 有限体積法に基づく離散化が実現されているのか,
OpenFOAM(R) ソースコード入門 pt1 熱伝導方程式の解法から有限体積法の実装について考える 前編 : 有限体積法の基礎確認 2013/11/17 オープンCAE 勉強会 @ 富山富山県立大学中川慎二 * OpenFOAM のソースコードでは, 基礎式を偏微分方程式の形で記述する.OpenFOAM 内部では, 有限体積法を使ってこの微分方程式を解いている. どのようにして, 有限体積法に基づく離散化が実現されているのか,
NS NS Scalar turbulence 5 6 FEM NS Mesh (A )
 22 3 2 1 2 2 2 3 3 4 NS 4 4.1 NS............ 5 5 Scalar turbulence 5 6 FEM 5 6.1 NS.................................... 6 6.2 Mes A )................................... 6 6.3.....................................
22 3 2 1 2 2 2 3 3 4 NS 4 4.1 NS............ 5 5 Scalar turbulence 5 6 FEM 5 6.1 NS.................................... 6 6.2 Mes A )................................... 6 6.3.....................................
Microsoft PowerPoint - elast.ppt [互換モード]
![Microsoft PowerPoint - elast.ppt [互換モード] Microsoft PowerPoint - elast.ppt [互換モード]](/thumbs/82/86104681.jpg) 弾性力学入門 年夏学期 中島研吾 科学技術計算 Ⅰ(48-7) コンピュータ科学特別講義 Ⅰ(48-4) elast 弾性力学 弾性力学の対象 応力 弾性力学の支配方程式 elast 3 弾性力学 連続体力学 (Continuum Mechanics) 固体力学 (Solid Mechanics) の一部 弾性体 (lastic Material) を対象 弾性論 (Theor of lasticit)
弾性力学入門 年夏学期 中島研吾 科学技術計算 Ⅰ(48-7) コンピュータ科学特別講義 Ⅰ(48-4) elast 弾性力学 弾性力学の対象 応力 弾性力学の支配方程式 elast 3 弾性力学 連続体力学 (Continuum Mechanics) 固体力学 (Solid Mechanics) の一部 弾性体 (lastic Material) を対象 弾性論 (Theor of lasticit)
微分方程式による現象記述と解きかた
 微分方程式による現象記述と解きかた 土木工学 : 公共諸施設 構造物の有用目的にむけた合理的な実現をはかる方法 ( 技術 ) に関する学 橋梁 トンネル ダム 道路 港湾 治水利水施設 安全化 利便化 快適化 合法則的 経済的 自然および人口素材によって作られた 質量保存則 構造物の自然的な性質 作用 ( 外力による応答 ) エネルギー則 の解明 社会的諸現象のうち マスとしての移動 流通 運動量則
微分方程式による現象記述と解きかた 土木工学 : 公共諸施設 構造物の有用目的にむけた合理的な実現をはかる方法 ( 技術 ) に関する学 橋梁 トンネル ダム 道路 港湾 治水利水施設 安全化 利便化 快適化 合法則的 経済的 自然および人口素材によって作られた 質量保存則 構造物の自然的な性質 作用 ( 外力による応答 ) エネルギー則 の解明 社会的諸現象のうち マスとしての移動 流通 運動量則
PowerPoint Presentation
 応用数学 Ⅱ (7) 7 連立微分方程式の立て方と解法. 高階微分方程式による解法. ベクトル微分方程式による解法 3. 演算子による解法 連立微分方程式 未知数が複数個あり, 未知数の数だけ微分方程式が与えられている場合, これらを連立微分方程式という. d d 解法 () 高階微分方程式化による解法 つの方程式から つの未知数を消去して, 未知数が つの方程式に変換 のみの方程式にするために,
応用数学 Ⅱ (7) 7 連立微分方程式の立て方と解法. 高階微分方程式による解法. ベクトル微分方程式による解法 3. 演算子による解法 連立微分方程式 未知数が複数個あり, 未知数の数だけ微分方程式が与えられている場合, これらを連立微分方程式という. d d 解法 () 高階微分方程式化による解法 つの方程式から つの未知数を消去して, 未知数が つの方程式に変換 のみの方程式にするために,
Microsoft PowerPoint - NA03-09black.ppt
 きょうの講義 数値 記号処理 2003.2.6 櫻井彰人 NumSymbol@soft.ae.keo.ac.jp http://www.sakura.comp.ae.keo.ac.jp/ 数値計算手法の定石 多項式近似 ( 復習 )» 誤差と手間の解析も 漸化式» 非線型方程式の求解 数値演算上の誤差 数値計算上の誤差 打ち切り誤差 (truncaton error)» 使う公式を有限項で打ち切る
きょうの講義 数値 記号処理 2003.2.6 櫻井彰人 NumSymbol@soft.ae.keo.ac.jp http://www.sakura.comp.ae.keo.ac.jp/ 数値計算手法の定石 多項式近似 ( 復習 )» 誤差と手間の解析も 漸化式» 非線型方程式の求解 数値演算上の誤差 数値計算上の誤差 打ち切り誤差 (truncaton error)» 使う公式を有限項で打ち切る
Microsoft PowerPoint - 2_FrontISTRと利用可能なソフトウェア.pptx
 東京大学本郷キャンパス 工学部8号館2階222中会議室 13:30-14:00 FrontISTRと利用可能なソフトウェア 2017年4月28日 第35回FrontISTR研究会 FrontISTRの並列計算ハンズオン 精度検証から並列性能評価まで 観測された物理現象 物理モデル ( 支配方程式 ) 連続体の運動を支配する偏微分方程式 離散化手法 ( 有限要素法, 差分法など ) 代数的な数理モデル
東京大学本郷キャンパス 工学部8号館2階222中会議室 13:30-14:00 FrontISTRと利用可能なソフトウェア 2017年4月28日 第35回FrontISTR研究会 FrontISTRの並列計算ハンズオン 精度検証から並列性能評価まで 観測された物理現象 物理モデル ( 支配方程式 ) 連続体の運動を支配する偏微分方程式 離散化手法 ( 有限要素法, 差分法など ) 代数的な数理モデル
DVIOUT-SS_Ma
 第 章 微分方程式 ニュートンはリンゴが落ちるのを見て万有引力を発見した という有名な逸話があります 無重力の宇宙船の中ではリンゴは落ちないで静止していることを考えると 重力が働くと始め静止しているものが動き出して そのスピードはどんどん大きくなる つまり速度の変化が現れることがわかります 速度は一般に時間と共に変化します 速度の瞬間的変化の割合を加速度といい で定義しましょう 速度が変化する, つまり加速度がでなくなるためにはその原因があり
第 章 微分方程式 ニュートンはリンゴが落ちるのを見て万有引力を発見した という有名な逸話があります 無重力の宇宙船の中ではリンゴは落ちないで静止していることを考えると 重力が働くと始め静止しているものが動き出して そのスピードはどんどん大きくなる つまり速度の変化が現れることがわかります 速度は一般に時間と共に変化します 速度の瞬間的変化の割合を加速度といい で定義しましょう 速度が変化する, つまり加速度がでなくなるためにはその原因があり
Microsoft PowerPoint - Lec17 [互換モード]
![Microsoft PowerPoint - Lec17 [互換モード] Microsoft PowerPoint - Lec17 [互換モード]](/thumbs/88/115805286.jpg) 情報デザイン専攻 画像情報処理論及び演習 - フィルタ処理 エッジ強調 - 差分法 変分法と平滑化 エッジ S Yoszw: s@re.p 今日の授業内容 www.re.p/rc/yoszw/ecres/e.ml www.re.p/rc/yoszw/ecres/ec7.p. 勾配とエッジの基礎 : 差分法.. plcと拡散方程式の基礎 : 変分法. 第 6 回講義水曜日 限教室 68 吉澤信 s@re.p
情報デザイン専攻 画像情報処理論及び演習 - フィルタ処理 エッジ強調 - 差分法 変分法と平滑化 エッジ S Yoszw: s@re.p 今日の授業内容 www.re.p/rc/yoszw/ecres/e.ml www.re.p/rc/yoszw/ecres/ec7.p. 勾配とエッジの基礎 : 差分法.. plcと拡散方程式の基礎 : 変分法. 第 6 回講義水曜日 限教室 68 吉澤信 s@re.p
PowerPoint Presentation
 付録 2 2 次元アフィン変換 直交変換 たたみ込み 1.2 次元のアフィン変換 座標 (x,y ) を (x,y) に移すことを 2 次元での変換. 特に, 変換が と書けるとき, アフィン変換, アフィン変換は, その 1 次の項による変換 と 0 次の項による変換 アフィン変換 0 次の項は平行移動 1 次の項は座標 (x, y ) をベクトルと考えて とすれば このようなもの 2 次元ベクトルの線形写像
付録 2 2 次元アフィン変換 直交変換 たたみ込み 1.2 次元のアフィン変換 座標 (x,y ) を (x,y) に移すことを 2 次元での変換. 特に, 変換が と書けるとき, アフィン変換, アフィン変換は, その 1 次の項による変換 と 0 次の項による変換 アフィン変換 0 次の項は平行移動 1 次の項は座標 (x, y ) をベクトルと考えて とすれば このようなもの 2 次元ベクトルの線形写像
Laplace2.rtf
 =0 ラプラスの方程式は 階の微分方程式で, 一般的に3つの座標変数をもつ. ここでは, 直角座標系, 円筒座標系, 球座標系におけるラプラスの方程式の解き方を説明しよう. 座標変数ごとに方程式を分離し, それを解いていく方法は変数分離法と呼ばれる. 変数分離解と固有関数展開法. 直角座標系における 3 次元の偏微分方程式 = x + y + z =0 (.) を解くために,x, y, z について互いに独立な関数の積で成り立っていると考え,
=0 ラプラスの方程式は 階の微分方程式で, 一般的に3つの座標変数をもつ. ここでは, 直角座標系, 円筒座標系, 球座標系におけるラプラスの方程式の解き方を説明しよう. 座標変数ごとに方程式を分離し, それを解いていく方法は変数分離法と呼ばれる. 変数分離解と固有関数展開法. 直角座標系における 3 次元の偏微分方程式 = x + y + z =0 (.) を解くために,x, y, z について互いに独立な関数の積で成り立っていると考え,
テンソル ( その ) テンソル ( その ) スカラー ( 階のテンソル ) スカラー ( 階のテンソル ) 階数 ベクトル ( 階のテンソル ) ベクトル ( 階のテンソル ) 行列表現 シンボリック表現 [ ]
![テンソル ( その ) テンソル ( その ) スカラー ( 階のテンソル ) スカラー ( 階のテンソル ) 階数 ベクトル ( 階のテンソル ) ベクトル ( 階のテンソル ) 行列表現 シンボリック表現 [ ] テンソル ( その ) テンソル ( その ) スカラー ( 階のテンソル ) スカラー ( 階のテンソル ) 階数 ベクトル ( 階のテンソル ) ベクトル ( 階のテンソル ) 行列表現 シンボリック表現 [ ]](/thumbs/93/113587990.jpg) Tsor th-ordr tsor by dcl xprsso m m Lm m k m k L mk kk quott rul by symbolc xprsso Lk X thrd-ordr tsor cotrcto j j Copyrght s rsrvd. No prt of ths documt my b rproducd for proft. テンソル ( その ) テンソル ( その
Tsor th-ordr tsor by dcl xprsso m m Lm m k m k L mk kk quott rul by symbolc xprsso Lk X thrd-ordr tsor cotrcto j j Copyrght s rsrvd. No prt of ths documt my b rproducd for proft. テンソル ( その ) テンソル ( その
5-仮想仕事式と種々の応力.ppt
 1 以上, 運動の変数についての話を終える. 次は再び力の変数に戻る. その前に, まず次の話が唐突と思われないように 以下は前置き. 先に, 力の変数と運動の変数には対応関係があって, 適当な内積演算によって仕事量を表す ことを述べた. 実は,Cauchy 応力と速度勾配テンソル ( あるいは変位勾配テンソル ) を用いると, それらの内積は内部仮想仕事を表していて, そして, それは外力がなす仮想仕事に等しいという
1 以上, 運動の変数についての話を終える. 次は再び力の変数に戻る. その前に, まず次の話が唐突と思われないように 以下は前置き. 先に, 力の変数と運動の変数には対応関係があって, 適当な内積演算によって仕事量を表す ことを述べた. 実は,Cauchy 応力と速度勾配テンソル ( あるいは変位勾配テンソル ) を用いると, それらの内積は内部仮想仕事を表していて, そして, それは外力がなす仮想仕事に等しいという
Microsoft PowerPoint - 熱力学Ⅱ2FreeEnergy2012HP.ppt [互換モード]
![Microsoft PowerPoint - 熱力学Ⅱ2FreeEnergy2012HP.ppt [互換モード] Microsoft PowerPoint - 熱力学Ⅱ2FreeEnergy2012HP.ppt [互換モード]](/thumbs/79/80168709.jpg) 熱力学 Ⅱ 第 章自由エネルギー システム情報工学研究科 構造エネルギー工学専攻 金子暁子 問題 ( 解答 ). 熱量 Q をある系に与えたところ, 系の体積は膨張し, 温度は上昇した. () 熱量 Q は何に変化したか. () またこのとき系の体積がV よりV に変化した.( 圧力は変化無し.) 内部エネルギーはどのように表されるか. また, このときのp-V 線図を示しなさい.. 不可逆過程の例を
熱力学 Ⅱ 第 章自由エネルギー システム情報工学研究科 構造エネルギー工学専攻 金子暁子 問題 ( 解答 ). 熱量 Q をある系に与えたところ, 系の体積は膨張し, 温度は上昇した. () 熱量 Q は何に変化したか. () またこのとき系の体積がV よりV に変化した.( 圧力は変化無し.) 内部エネルギーはどのように表されるか. また, このときのp-V 線図を示しなさい.. 不可逆過程の例を
Microsoft Word - thesis.doc
 剛体の基礎理論 -. 剛体の基礎理論初めに本論文で大域的に使用する記号を定義する. 使用する記号トルク撃力力角運動量角速度姿勢対角化された慣性テンソル慣性テンソル運動量速度位置質量時間 J W f F P p .. 質点の並進運動 質点は位置 と速度 P を用いる. ニュートンの運動方程式 という状態を持つ. 但し ここでは速度ではなく運動量 F P F.... より質点の運動は既に明らかであり 質点の状態ベクトル
剛体の基礎理論 -. 剛体の基礎理論初めに本論文で大域的に使用する記号を定義する. 使用する記号トルク撃力力角運動量角速度姿勢対角化された慣性テンソル慣性テンソル運動量速度位置質量時間 J W f F P p .. 質点の並進運動 質点は位置 と速度 P を用いる. ニュートンの運動方程式 という状態を持つ. 但し ここでは速度ではなく運動量 F P F.... より質点の運動は既に明らかであり 質点の状態ベクトル
応用数学Ⅱ 偏微分方程式(2) 波動方程式(12/13)
 偏微分方程式. 偏微分方程式の形 偏微分 偏導関数 つの独立変数 をもつ関数 があるとき 変数 が一定値をとって だけが変化したとす ると は だけの関数となる このとき を について微分して得られる関数を 関数 の に関する 偏微分係数 略して偏微分 あるいは偏導関数 pil deiie といい 次のように表される についても同様な偏微分を定義できる あるいは あるいは - あるいは あるいは -
偏微分方程式. 偏微分方程式の形 偏微分 偏導関数 つの独立変数 をもつ関数 があるとき 変数 が一定値をとって だけが変化したとす ると は だけの関数となる このとき を について微分して得られる関数を 関数 の に関する 偏微分係数 略して偏微分 あるいは偏導関数 pil deiie といい 次のように表される についても同様な偏微分を定義できる あるいは あるいは - あるいは あるいは -
Microsoft PowerPoint - H22制御工学I-2回.ppt
 制御工学 I 第二回ラプラス変換 平成 年 4 月 9 日 /4/9 授業の予定 制御工学概論 ( 回 ) 制御技術は現在様々な工学分野において重要な基本技術となっている 工学における制御工学の位置づけと歴史について説明する さらに 制御システムの基本構成と種類を紹介する ラプラス変換 ( 回 ) 制御工学 特に古典制御ではラプラス変換が重要な役割を果たしている ラプラス変換と逆ラプラス変換の定義を紹介し
制御工学 I 第二回ラプラス変換 平成 年 4 月 9 日 /4/9 授業の予定 制御工学概論 ( 回 ) 制御技術は現在様々な工学分野において重要な基本技術となっている 工学における制御工学の位置づけと歴史について説明する さらに 制御システムの基本構成と種類を紹介する ラプラス変換 ( 回 ) 制御工学 特に古典制御ではラプラス変換が重要な役割を果たしている ラプラス変換と逆ラプラス変換の定義を紹介し
0 21 カラー反射率 slope aspect 図 2.9: 復元結果例 2.4 画像生成技術としての計算フォトグラフィ 3 次元情報を復元することにより, 画像生成 ( レンダリング ) に応用することが可能である. 近年, コンピュータにより, カメラで直接得られない画像を生成する技術分野が生
 0 21 カラー反射率 slope aspect 図 2.9: 復元結果例 2.4 画像生成技術としての計算フォトグラフィ 3 次元情報を復元することにより, 画像生成 ( レンダリング ) に応用することが可能である. 近年, コンピュータにより, カメラで直接得られない画像を生成する技術分野が生まれ, コンピューテーショナルフォトグラフィ ( 計算フォトグラフィ ) と呼ばれている.3 次元画像認識技術の計算フォトグラフィへの応用として,
0 21 カラー反射率 slope aspect 図 2.9: 復元結果例 2.4 画像生成技術としての計算フォトグラフィ 3 次元情報を復元することにより, 画像生成 ( レンダリング ) に応用することが可能である. 近年, コンピュータにより, カメラで直接得られない画像を生成する技術分野が生まれ, コンピューテーショナルフォトグラフィ ( 計算フォトグラフィ ) と呼ばれている.3 次元画像認識技術の計算フォトグラフィへの応用として,
NumericalProg09
 数値解析および プログラミング演習 [08 第 9 回目 ] の解法 - 4. Ruge-Kua( ルンゲ クッタ 法 Ruge-Kua-Gill( ルンゲ クッタ ジル / ギル 法 5. 多段解法 解法の対象 常微分方程式 d( d 初期値条件 (, の変化に応じて変化する の値を求める. ( 0 ( 0 と 0 は,give 0 常微分方程式の初期値問題 と言う. 3 Ruge-Kua 法の導出
数値解析および プログラミング演習 [08 第 9 回目 ] の解法 - 4. Ruge-Kua( ルンゲ クッタ 法 Ruge-Kua-Gill( ルンゲ クッタ ジル / ギル 法 5. 多段解法 解法の対象 常微分方程式 d( d 初期値条件 (, の変化に応じて変化する の値を求める. ( 0 ( 0 と 0 は,give 0 常微分方程式の初期値問題 と言う. 3 Ruge-Kua 法の導出
1.民営化
 参考資料 最小二乗法 数学的性質 経済統計分析 3 年度秋学期 回帰分析と最小二乗法 被説明変数 の動きを説明変数 の動きで説明 = 回帰分析 説明変数がつ 単回帰 説明変数がつ以上 重回帰 被説明変数 従属変数 係数 定数項傾き 説明変数 独立変数 残差... で説明できる部分 説明できない部分 説明できない部分が小さくなるように回帰式の係数 を推定する有力な方法 = 最小二乗法 最小二乗法による回帰の考え方
参考資料 最小二乗法 数学的性質 経済統計分析 3 年度秋学期 回帰分析と最小二乗法 被説明変数 の動きを説明変数 の動きで説明 = 回帰分析 説明変数がつ 単回帰 説明変数がつ以上 重回帰 被説明変数 従属変数 係数 定数項傾き 説明変数 独立変数 残差... で説明できる部分 説明できない部分 説明できない部分が小さくなるように回帰式の係数 を推定する有力な方法 = 最小二乗法 最小二乗法による回帰の考え方
数学 ⅡB < 公理 > 公理を論拠に定義を用いて定理を証明する 1 大小関係の公理 順序 (a > b, a = b, a > b 1 つ成立 a > b, b > c a > c 成立 ) 順序と演算 (a > b a + c > b + c (a > b, c > 0 ac > bc) 2 図
 数学 Ⅱ < 公理 > 公理を論拠に定義を用いて定理を証明する 大小関係の公理 順序 >, =, > つ成立 >, > > 成立 順序と演算 > + > + >, > > 図形の公理 平行線の性質 錯角 同位角 三角形の合同条件 三角形の合同相似 量の公理 角の大きさ 線分の長さ < 空間における座漂とベクトル > ベクトルの演算 和 差 実数倍については 文字の計算と同様 ベクトルの成分表示 平面ベクトル
数学 Ⅱ < 公理 > 公理を論拠に定義を用いて定理を証明する 大小関係の公理 順序 >, =, > つ成立 >, > > 成立 順序と演算 > + > + >, > > 図形の公理 平行線の性質 錯角 同位角 三角形の合同条件 三角形の合同相似 量の公理 角の大きさ 線分の長さ < 空間における座漂とベクトル > ベクトルの演算 和 差 実数倍については 文字の計算と同様 ベクトルの成分表示 平面ベクトル
...Y..FEM.pm5
 . 剛塑性有限要素法 名古屋大学大学院工学研究科. はじめに. 剛塑性体の構成式.. 降伏条件.. 構成方程式 ([D] マトリックス ). 節点速度 ひずみ速度関係..[B] マトリックス.. 四角形一次要素の [B] マトリックス.4 4 仮想仕事の原理 ( 剛性マトリックス ([K] マトリックス )).5 非線形方程式の解法.5. 直接代入法.5.wto-Raphso 法.6 非圧縮性の拘束と数値積分.7
. 剛塑性有限要素法 名古屋大学大学院工学研究科. はじめに. 剛塑性体の構成式.. 降伏条件.. 構成方程式 ([D] マトリックス ). 節点速度 ひずみ速度関係..[B] マトリックス.. 四角形一次要素の [B] マトリックス.4 4 仮想仕事の原理 ( 剛性マトリックス ([K] マトリックス )).5 非線形方程式の解法.5. 直接代入法.5.wto-Raphso 法.6 非圧縮性の拘束と数値積分.7
以下 変数の上のドットは時間に関する微分を表わしている (ex. 2 dx d x x, x 2 dt dt ) 付録 E 非線形微分方程式の平衡点の安定性解析 E-1) 非線形方程式の線形近似特に言及してこなかったが これまでは線形微分方程式 ( x や x, x などがすべて 1 次で なおかつ
 以下 変数の上のドットは時間に関する微分を表わしている (e. d d, dt dt ) 付録 E 非線形微分方程式の平衡点の安定性解析 E-) 非線形方程式の線形近似特に言及してこなかったが これまでは線形微分方程式 ( や, などがすべて 次で なおかつそれらの係数が定数であるような微分方程式 ) に対して安定性の解析を行ってきた しかしながら 実際には非線形の微分方程式で記述される現象も多く存在する
以下 変数の上のドットは時間に関する微分を表わしている (e. d d, dt dt ) 付録 E 非線形微分方程式の平衡点の安定性解析 E-) 非線形方程式の線形近似特に言及してこなかったが これまでは線形微分方程式 ( や, などがすべて 次で なおかつそれらの係数が定数であるような微分方程式 ) に対して安定性の解析を行ってきた しかしながら 実際には非線形の微分方程式で記述される現象も多く存在する
Microsoft Word - mathtext8.doc
 8 章偏微分と重積分 8. 偏微分とは これまで微分を考える際 関数は f という形で 関数値がつの変数 に依存している場合のみを扱ってきました しかし一般に変数はつとは決まっておらず f のように 複数の変数を持つ関数も考えなければなりません そ こでこの節では今まで学んできた微分を一般化させ 複数の変数に対応した偏微分と呼ばれるものについて説明します これまでの微分を偏微分と区別したいとき 常微分という呼び方を用います
8 章偏微分と重積分 8. 偏微分とは これまで微分を考える際 関数は f という形で 関数値がつの変数 に依存している場合のみを扱ってきました しかし一般に変数はつとは決まっておらず f のように 複数の変数を持つ関数も考えなければなりません そ こでこの節では今まで学んできた微分を一般化させ 複数の変数に対応した偏微分と呼ばれるものについて説明します これまでの微分を偏微分と区別したいとき 常微分という呼び方を用います
Stage 並列プログラミングを習得するためには : 1 計算機リテラシ, プログラミング言語 2 基本的な数値解析 3 実アプリケーション ( 例えば有限要素法, 分子動力学 ) のプログラミング 4 その並列化 という 4 つの段階 (stage) が必要である 本人材育成プログラムでは1~4を
 コンピュータ科学特別講義 科学技術計算プログラミング I ( 有限要素法 ) 中島研吾 東京大学情報基盤センター 1. はじめに本稿では,2008 年度冬学期に実施した, コンピュータ科学特別講義 I 科学技術計算プログラミング ( 有限要素法 ) について紹介する 計算科学 工学, ハードウェアの急速な進歩, 発達を背景に, 第 3 の科学 としての大規模並列シミュレーションへの期待は, 産学において一層高まっている
コンピュータ科学特別講義 科学技術計算プログラミング I ( 有限要素法 ) 中島研吾 東京大学情報基盤センター 1. はじめに本稿では,2008 年度冬学期に実施した, コンピュータ科学特別講義 I 科学技術計算プログラミング ( 有限要素法 ) について紹介する 計算科学 工学, ハードウェアの急速な進歩, 発達を背景に, 第 3 の科学 としての大規模並列シミュレーションへの期待は, 産学において一層高まっている
喨微勃挹稉弑
 == 全微分方程式 == 全微分とは 変数の関数 z=f(, ) について,, の増分を Δ, Δ とするとき, z の増分 Δz は Δz z Δ+ z Δ で表されます. この式において, Δ 0, Δ 0 となる極限を形式的に dz= z d+ z d (1) で表し, dz を z の全微分といいます. z は z の に関する偏導関数で, を定数と見なし て, で微分したものを表し, 方向の傾きに対応します.
== 全微分方程式 == 全微分とは 変数の関数 z=f(, ) について,, の増分を Δ, Δ とするとき, z の増分 Δz は Δz z Δ+ z Δ で表されます. この式において, Δ 0, Δ 0 となる極限を形式的に dz= z d+ z d (1) で表し, dz を z の全微分といいます. z は z の に関する偏導関数で, を定数と見なし て, で微分したものを表し, 方向の傾きに対応します.
多次元レーザー分光で探る凝縮分子系の超高速動力学
 波動方程式と量子力学 谷村吉隆 京都大学理学研究科化学専攻 http:theochem.kuchem.kyoto-u.ac.jp TA: 岩元佑樹 iwamoto.y@kuchem.kyoto-u.ac.jp ベクトルと行列の作法 A 列ベクトル c = c c 行ベクトル A = [ c c c ] 転置ベクトル T A = [ c c c ] AA 内積 c AA = [ c c c ] c =
波動方程式と量子力学 谷村吉隆 京都大学理学研究科化学専攻 http:theochem.kuchem.kyoto-u.ac.jp TA: 岩元佑樹 iwamoto.y@kuchem.kyoto-u.ac.jp ベクトルと行列の作法 A 列ベクトル c = c c 行ベクトル A = [ c c c ] 転置ベクトル T A = [ c c c ] AA 内積 c AA = [ c c c ] c =
入門講座
 第 8 章弾性歪エネルギー評価法 () () 8- Khhtun の弾性歪エネルギ- 評価ここでも簡単のため A-B 元系における不規則相の整合相分離を考え この相分解組織の弾性歪エネルギーを評価する 手順は ステップ ) まず位置 の関数として与えられる濃度場 () を用いて egen 歪場 ε () を定義する ステップ ) 次に全歪場 ε () を均一全歪 ε とそこからの変動量 δε ()
第 8 章弾性歪エネルギー評価法 () () 8- Khhtun の弾性歪エネルギ- 評価ここでも簡単のため A-B 元系における不規則相の整合相分離を考え この相分解組織の弾性歪エネルギーを評価する 手順は ステップ ) まず位置 の関数として与えられる濃度場 () を用いて egen 歪場 ε () を定義する ステップ ) 次に全歪場 ε () を均一全歪 ε とそこからの変動量 δε ()
3 数値解の特性 3.1 CFL 条件 を 前の章では 波動方程式 f x= x0 = f x= x0 t f c x f =0 [1] c f 0 x= x 0 x 0 f x= x0 x 2 x 2 t [2] のように差分化して数値解を求めた ここでは このようにして得られた数値解の性質を 考
![3 数値解の特性 3.1 CFL 条件 を 前の章では 波動方程式 f x= x0 = f x= x0 t f c x f =0 [1] c f 0 x= x 0 x 0 f x= x0 x 2 x 2 t [2] のように差分化して数値解を求めた ここでは このようにして得られた数値解の性質を 考 3 数値解の特性 3.1 CFL 条件 を 前の章では 波動方程式 f x= x0 = f x= x0 t f c x f =0 [1] c f 0 x= x 0 x 0 f x= x0 x 2 x 2 t [2] のように差分化して数値解を求めた ここでは このようにして得られた数値解の性質を 考](/thumbs/103/158269281.jpg) 3 数値解の特性 3.1 CFL 条件 を 前の章では 波動方程式 f x= x = f x= x t f c x f = [1] c f x= x f x= x 2 2 t [2] のように差分化して数値解を求めた ここでは このようにして得られた数値解の性質を 考える まず 初期時刻 t=t に f =R f exp [ik x ] [3] のような波動を与えたとき どのように時間変化するか調べる
3 数値解の特性 3.1 CFL 条件 を 前の章では 波動方程式 f x= x = f x= x t f c x f = [1] c f x= x f x= x 2 2 t [2] のように差分化して数値解を求めた ここでは このようにして得られた数値解の性質を 考える まず 初期時刻 t=t に f =R f exp [ik x ] [3] のような波動を与えたとき どのように時間変化するか調べる
Autodesk Inventor Skill Builders Autodesk Inventor 2010 構造解析の精度改良 メッシュリファインメントによる収束計算 予想作業時間:15 分 対象のバージョン:Inventor 2010 もしくはそれ以降のバージョン シミュレーションを設定する際
 Autodesk Inventor Skill Builders Autodesk Inventor 2010 構造解析の精度改良 メッシュリファインメントによる収束計算 予想作業時間:15 分 対象のバージョン:Inventor 2010 もしくはそれ以降のバージョン シミュレーションを設定する際に 収束判定に関するデフォルトの設定をそのまま使うか 修正をします 応力解析ソルバーでは計算の終了を判断するときにこの設定を使います
Autodesk Inventor Skill Builders Autodesk Inventor 2010 構造解析の精度改良 メッシュリファインメントによる収束計算 予想作業時間:15 分 対象のバージョン:Inventor 2010 もしくはそれ以降のバージョン シミュレーションを設定する際に 収束判定に関するデフォルトの設定をそのまま使うか 修正をします 応力解析ソルバーでは計算の終了を判断するときにこの設定を使います
Microsoft Word - 5章摂動法.doc
 5 章摂動法 ( 次の Moller-Plesset (MP) 法のために ) // 水素原子など 電子系を除いては 原子系の Schrödiger 方程式を解析的に解くことはできない 分子系の Schrödiger 方程式の正確な数値解を求めることも困難である そこで Hartree-Fock(H-F) 法を導入した H-F 法は Schrödiger 方程式が与える全エネルギーの 99% を再現することができる優れた近似方法である
5 章摂動法 ( 次の Moller-Plesset (MP) 法のために ) // 水素原子など 電子系を除いては 原子系の Schrödiger 方程式を解析的に解くことはできない 分子系の Schrödiger 方程式の正確な数値解を求めることも困難である そこで Hartree-Fock(H-F) 法を導入した H-F 法は Schrödiger 方程式が与える全エネルギーの 99% を再現することができる優れた近似方法である
PowerPoint Presentation
 06 年 8 月 日 ( 月 )-6 日 ( 金 ) 千葉大学総合校舎 号館 4 階情報演習室 宇宙磁気流体 プラズマシミュレーションサマースクール 差分法の基礎 三好隆博 広島大学大学院理学研究科 時限目の目標 線形移流方程式 コンピュータ を計算機で解く! 内容 はじめに 差分法 移流方程式の差分法 高次精度風上差分法 はじめに はじめに 微分方程式 未知関数とその導関数を含む方程式 自然現象などを記述する基礎方程式
06 年 8 月 日 ( 月 )-6 日 ( 金 ) 千葉大学総合校舎 号館 4 階情報演習室 宇宙磁気流体 プラズマシミュレーションサマースクール 差分法の基礎 三好隆博 広島大学大学院理学研究科 時限目の目標 線形移流方程式 コンピュータ を計算機で解く! 内容 はじめに 差分法 移流方程式の差分法 高次精度風上差分法 はじめに はじめに 微分方程式 未知関数とその導関数を含む方程式 自然現象などを記述する基礎方程式
<4D F736F F D2097CD8A7793FC96E582BD82ED82DD8A E6318FCD2E646F63>
 - 第 章たわみ角法の基本式 ポイント : たわみ角法の基本式を理解する たわみ角法の基本式を梁の微分方程式より求める 本章では たわみ角法の基本式を導くことにする 基本式の誘導法は各種あるが ここでは 梁の微分方程式を解いて基本式を求める方法を採用する この本で使用する座標系は 右手 右ネジの法則に従った座標を用いる また ひとつの部材では 図 - に示すように部材の左端の 点を原点とし 軸線を
- 第 章たわみ角法の基本式 ポイント : たわみ角法の基本式を理解する たわみ角法の基本式を梁の微分方程式より求める 本章では たわみ角法の基本式を導くことにする 基本式の誘導法は各種あるが ここでは 梁の微分方程式を解いて基本式を求める方法を採用する この本で使用する座標系は 右手 右ネジの法則に従った座標を用いる また ひとつの部材では 図 - に示すように部材の左端の 点を原点とし 軸線を
PowerPoint Presentation
 Non-linea factue mechanics き裂先端付近の塑性変形 塑性域 R 破壊進行領域応カ特異場 Ω R R Hutchinson, Rice and Rosengen 全ひずみ塑性理論に基づいた解析 現段階のひずみは 除荷がないとすると現段階の応力で一義的に決まる 単純引張り時の応カーひずみ関係 ( 構成方程式 ): ( ) ( ) n () y y y ここで α,n 定数, /
Non-linea factue mechanics き裂先端付近の塑性変形 塑性域 R 破壊進行領域応カ特異場 Ω R R Hutchinson, Rice and Rosengen 全ひずみ塑性理論に基づいた解析 現段階のひずみは 除荷がないとすると現段階の応力で一義的に決まる 単純引張り時の応カーひずみ関係 ( 構成方程式 ): ( ) ( ) n () y y y ここで α,n 定数, /
微分方程式 モデリングとシミュレーション
 1 微分方程式モデリングとシミュレーション 2018 年度 2 質点の運動のモデル化 粒子と粒子に働く力 粒子の運動 粒子の位置の時間変化 粒子の位置の変化の割合 速度 速度の変化の割合 加速度 力と加速度の結び付け Newtonの運動方程式 : 微分方程式 解は 時間の関数としての位置 3 Newton の運動方程式 質点の運動は Newton の運動方程式で記述される 加速度は力に比例する 2
1 微分方程式モデリングとシミュレーション 2018 年度 2 質点の運動のモデル化 粒子と粒子に働く力 粒子の運動 粒子の位置の時間変化 粒子の位置の変化の割合 速度 速度の変化の割合 加速度 力と加速度の結び付け Newtonの運動方程式 : 微分方程式 解は 時間の関数としての位置 3 Newton の運動方程式 質点の運動は Newton の運動方程式で記述される 加速度は力に比例する 2
オープン CAE 関東 数値流体力学 輪講 第 4 回 第 3 章 : 乱流とそのモデリング (3) [3.5~3.7.1 p.64~75] 日時 :2013 年 11 月 10 日 14:00~ 場所 : 日本 新宿 2013/11/10 数値流体力学 輪講第 4 回 1
![オープン CAE 関東 数値流体力学 輪講 第 4 回 第 3 章 : 乱流とそのモデリング (3) [3.5~3.7.1 p.64~75] 日時 :2013 年 11 月 10 日 14:00~ 場所 : 日本 新宿 2013/11/10 数値流体力学 輪講第 4 回 1 オープン CAE 関東 数値流体力学 輪講 第 4 回 第 3 章 : 乱流とそのモデリング (3) [3.5~3.7.1 p.64~75] 日時 :2013 年 11 月 10 日 14:00~ 場所 : 日本 新宿 2013/11/10 数値流体力学 輪講第 4 回 1](/thumbs/98/136800732.jpg) オープン CAE 勉強会 @ 関東 数値流体力学 輪講 第 4 回 第 3 章 : 乱流とそのモデリング (3 [3.5~3.7.1 p.64~75] 日時 :2013 年 11 月 10 日 14:00~ 場所 : 日本 ESI@ 新宿 1 数値流体力学 輪講に関して 目的 数値流体力学の知識 ( 特に理論ベース を深め OpenFOAM の利用に役立てること 本輪講で学ぶもの 数値流体力学の理論や計算手法の概要
オープン CAE 勉強会 @ 関東 数値流体力学 輪講 第 4 回 第 3 章 : 乱流とそのモデリング (3 [3.5~3.7.1 p.64~75] 日時 :2013 年 11 月 10 日 14:00~ 場所 : 日本 ESI@ 新宿 1 数値流体力学 輪講に関して 目的 数値流体力学の知識 ( 特に理論ベース を深め OpenFOAM の利用に役立てること 本輪講で学ぶもの 数値流体力学の理論や計算手法の概要
PowerPoint プレゼンテーション
 工業数学 Ⅰ 第 7 章多変数関数の微分 2. 実多変数の実数値関数 千葉大学工学部機械工学科担当者武居昌宏 教科書 工科系の数学 (4) [ 単行本 ] マイベルク ファヘンアウア著 及川正行訳 出版社 : サイエンス社 (1996/12) ISBN-10: 4781907814 第 7 章多変数関数の微分 2. 実多変数の実数値関数 2.1 基礎 多変数の実数値関数変数が2つ以上の n 変数関数定義域がn
工業数学 Ⅰ 第 7 章多変数関数の微分 2. 実多変数の実数値関数 千葉大学工学部機械工学科担当者武居昌宏 教科書 工科系の数学 (4) [ 単行本 ] マイベルク ファヘンアウア著 及川正行訳 出版社 : サイエンス社 (1996/12) ISBN-10: 4781907814 第 7 章多変数関数の微分 2. 実多変数の実数値関数 2.1 基礎 多変数の実数値関数変数が2つ以上の n 変数関数定義域がn
例 e 指数関数的に減衰する信号を h( a < + a a すると, それらのラプラス変換は, H ( ) { e } e インパルス応答が h( a < ( ただし a >, U( ) { } となるシステムにステップ信号 ( y( のラプラス変換 Y () は, Y ( ) H ( ) X (
 第 週ラプラス変換 教科書 p.34~ 目標ラプラス変換の定義と意味を理解する フーリエ変換や Z 変換と並ぶ 信号解析やシステム設計における重要なツール ラプラス変換は波動現象や電気回路など様々な分野で 微分方程式を解くために利用されてきた ラプラス変換を用いることで微分方程式は代数方程式に変換される また 工学上使われる主要な関数のラプラス変換は簡単な形の関数で表されるので これを ラプラス変換表
第 週ラプラス変換 教科書 p.34~ 目標ラプラス変換の定義と意味を理解する フーリエ変換や Z 変換と並ぶ 信号解析やシステム設計における重要なツール ラプラス変換は波動現象や電気回路など様々な分野で 微分方程式を解くために利用されてきた ラプラス変換を用いることで微分方程式は代数方程式に変換される また 工学上使われる主要な関数のラプラス変換は簡単な形の関数で表されるので これを ラプラス変換表
Microsoft PowerPoint - 第7章(自然対流熱伝達 )_H27.ppt [互換モード]
![Microsoft PowerPoint - 第7章(自然対流熱伝達 )_H27.ppt [互換モード] Microsoft PowerPoint - 第7章(自然対流熱伝達 )_H27.ppt [互換モード]](/thumbs/94/118222251.jpg) 第 7 章自然対流熱伝達 伝熱工学の基礎 : 伝熱の基本要素 フーリエの法則 ニュートンの冷却則 次元定常熱伝導 : 熱伝導率 熱通過率 熱伝導方程式 次元定常熱伝導 : ラプラスの方程式 数値解析の基礎 非定常熱伝導 : 非定常熱伝導方程式 ラプラス変換 フーリエ数とビオ数 対流熱伝達の基礎 : 熱伝達率 速度境界層と温度境界層 層流境界層と乱流境界層 境界層厚さ 混合平均温度 強制対流熱伝達 :
第 7 章自然対流熱伝達 伝熱工学の基礎 : 伝熱の基本要素 フーリエの法則 ニュートンの冷却則 次元定常熱伝導 : 熱伝導率 熱通過率 熱伝導方程式 次元定常熱伝導 : ラプラスの方程式 数値解析の基礎 非定常熱伝導 : 非定常熱伝導方程式 ラプラス変換 フーリエ数とビオ数 対流熱伝達の基礎 : 熱伝達率 速度境界層と温度境界層 層流境界層と乱流境界層 境界層厚さ 混合平均温度 強制対流熱伝達 :
Microsoft Word - 断面諸量
 応用力学 Ⅱ 講義資料 / 断面諸量 断面諸量 断面 次 次モーメントの定義 図 - に示すような形状を有する横断面を考え その全断面積を とする いま任意に定めた直交座標軸 O-, をとり また図中の斜線部の微小面積要素を d とするとき d, d () で定義される, をそれぞれ与えられた横断面の 軸, 軸に関する断面 次モーメント (geometrcal moment of area) という
応用力学 Ⅱ 講義資料 / 断面諸量 断面諸量 断面 次 次モーメントの定義 図 - に示すような形状を有する横断面を考え その全断面積を とする いま任意に定めた直交座標軸 O-, をとり また図中の斜線部の微小面積要素を d とするとき d, d () で定義される, をそれぞれ与えられた横断面の 軸, 軸に関する断面 次モーメント (geometrcal moment of area) という
ベクトル公式.rtf
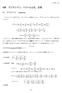 6 章ラプラシアン, ベクトル公式, 定理 6.1 ラプラシアン Laplacian φ はベクトル量である. そこでさらに発散をとると, φ はどういう形になるであろうか? φ = a + a + a φ a + a φ + a φ = φ + φ + φ = 2 φ + 2 φ 2 + 2 φ 2 2 φ = 2 φ 2 + 2 φ 2 + 2 φ 2 = 2 φ したがって,2 階の偏微分演算となる.
6 章ラプラシアン, ベクトル公式, 定理 6.1 ラプラシアン Laplacian φ はベクトル量である. そこでさらに発散をとると, φ はどういう形になるであろうか? φ = a + a + a φ a + a φ + a φ = φ + φ + φ = 2 φ + 2 φ 2 + 2 φ 2 2 φ = 2 φ 2 + 2 φ 2 + 2 φ 2 = 2 φ したがって,2 階の偏微分演算となる.
Microsoft Word - 201hyouka-tangen-1.doc
 数学 Ⅰ 評価規準の作成 ( 単元ごと ) 数学 Ⅰ の目標及び図形と計量について理解させ 基礎的な知識の習得と技能の習熟を図り それらを的確に活用する機能を伸ばすとともに 数学的な見方や考え方のよさを認識できるようにする 評価の観点の趣旨 式と不等式 二次関数及び図形と計量における考え方に関 心をもつとともに 数学的な見方や考え方のよさを認識し それらを事象の考察に活用しようとする 式と不等式 二次関数及び図形と計量における数学的な見
数学 Ⅰ 評価規準の作成 ( 単元ごと ) 数学 Ⅰ の目標及び図形と計量について理解させ 基礎的な知識の習得と技能の習熟を図り それらを的確に活用する機能を伸ばすとともに 数学的な見方や考え方のよさを認識できるようにする 評価の観点の趣旨 式と不等式 二次関数及び図形と計量における考え方に関 心をもつとともに 数学的な見方や考え方のよさを認識し それらを事象の考察に活用しようとする 式と不等式 二次関数及び図形と計量における数学的な見
差分スキーム 物理 化学 生物現象には微分方程式でモデル化される例が多い モデルを使って現実の現象をコンピュータ上で再現することをシミュレーション ( 数値シミュレーション コンピュータシミュレーション ) と呼ぶ そのためには 微分方程式をコンピュータ上で計算できる数値スキームで近似することが必要
 差分スキーム 物理 化学 生物現象には微分方程式でモデル化される例が多い モデルを使って現実の現象をコンピュータ上で再現することをシミュレーション ( 数値シミュレーション コンピュータシミュレーション ) と呼ぶ そのためには 微分方程式をコンピュータ上で計算できる数値スキームで近似することが必要になる その一つの方法が微分方程式を差分方程式におき直すことである 微分方程式の差分化 次の 1 次元境界値問題を考える
差分スキーム 物理 化学 生物現象には微分方程式でモデル化される例が多い モデルを使って現実の現象をコンピュータ上で再現することをシミュレーション ( 数値シミュレーション コンピュータシミュレーション ) と呼ぶ そのためには 微分方程式をコンピュータ上で計算できる数値スキームで近似することが必要になる その一つの方法が微分方程式を差分方程式におき直すことである 微分方程式の差分化 次の 1 次元境界値問題を考える
学習指導要領
 (1) 数と式 ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 絶対値の意味を理解し適切な処理することができる 例題 1-3 の絶対値をはずせ 展開公式 ( a + b ) ( a - b ) = a 2 - b 2 を利用して根号を含む分数の分母を有理化することができる 例題 5 5 + 2 の分母を有理化せよ 実数の整数部分と小数部分の表し方を理解している
(1) 数と式 ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 絶対値の意味を理解し適切な処理することができる 例題 1-3 の絶対値をはずせ 展開公式 ( a + b ) ( a - b ) = a 2 - b 2 を利用して根号を含む分数の分母を有理化することができる 例題 5 5 + 2 の分母を有理化せよ 実数の整数部分と小数部分の表し方を理解している
学習指導要領
 (1) いろいろな式 学習指導要領紅葉川高校学力スタンダードア式と証明展開の公式を用いて 3 乗に関わる式を展開すること ( ア ) 整式の乗法 除法 分数式の計算ができるようにする 三次の乗法公式及び因数分解の公式を理解し そ 3 次の因数分解の公式を理解し それらを用いて因数れらを用いて式の展開や因数分解をすること また 分解することができるようにする 整式の除法や分数式の四則計算について理解し
(1) いろいろな式 学習指導要領紅葉川高校学力スタンダードア式と証明展開の公式を用いて 3 乗に関わる式を展開すること ( ア ) 整式の乗法 除法 分数式の計算ができるようにする 三次の乗法公式及び因数分解の公式を理解し そ 3 次の因数分解の公式を理解し それらを用いて因数れらを用いて式の展開や因数分解をすること また 分解することができるようにする 整式の除法や分数式の四則計算について理解し
ニュートン重力理論.pptx
 3 ニュートン重力理論 1. ニュートン重力理論の基本 : 慣性系とガリレイ変換不変性 2. ニュートン重力理論の定式化 3. 等価原理 4. 流体力学方程式とその基礎 3.1 ニュートン重力理論の基本 u ニュートンの第一法則 = 力がかからなければ 等速直線運動を続ける u 等速直線運動に見える系を 慣性系 と呼ぶ ² 直線とはどんな空間の直線か? ニュートン理論では 3 次元ユークリッド空間
3 ニュートン重力理論 1. ニュートン重力理論の基本 : 慣性系とガリレイ変換不変性 2. ニュートン重力理論の定式化 3. 等価原理 4. 流体力学方程式とその基礎 3.1 ニュートン重力理論の基本 u ニュートンの第一法則 = 力がかからなければ 等速直線運動を続ける u 等速直線運動に見える系を 慣性系 と呼ぶ ² 直線とはどんな空間の直線か? ニュートン理論では 3 次元ユークリッド空間
Microsoft Word - 微分入門.doc
 基本公式 例題 0 定義式 f( ) 数 Ⅲ 微分入門 = の導関数を定義式にもとづいて計算しなさい 基本事項 ( f( ), g( ) が微分可能ならば ) y= f( ) g( ) のとき, y = y= f( ) g( ) h( ) のとき, y = ( f( ), g( ) が微分可能で, g( ) 0 ならば ) f( ) y = のとき, y = g ( ) とくに, y = のとき,
基本公式 例題 0 定義式 f( ) 数 Ⅲ 微分入門 = の導関数を定義式にもとづいて計算しなさい 基本事項 ( f( ), g( ) が微分可能ならば ) y= f( ) g( ) のとき, y = y= f( ) g( ) h( ) のとき, y = ( f( ), g( ) が微分可能で, g( ) 0 ならば ) f( ) y = のとき, y = g ( ) とくに, y = のとき,
Microsoft PowerPoint - Inoue-statistics [互換モード]
![Microsoft PowerPoint - Inoue-statistics [互換モード] Microsoft PowerPoint - Inoue-statistics [互換モード]](/thumbs/92/107910528.jpg) 誤差論 神戸大学大学院農学研究科 井上一哉 (Kazuya INOUE) 誤差論 2011 年度前期火曜クラス 1 講義内容 誤差と有効数字 (Slide No.2~8 Text p.76~78) 誤差の分布と標準偏差 (Slide No.9~18 Text p.78~80) 最確値とその誤差 (Slide No.19~25 Text p.80~81) 誤差の伝播 (Slide No.26~32 Text
誤差論 神戸大学大学院農学研究科 井上一哉 (Kazuya INOUE) 誤差論 2011 年度前期火曜クラス 1 講義内容 誤差と有効数字 (Slide No.2~8 Text p.76~78) 誤差の分布と標準偏差 (Slide No.9~18 Text p.78~80) 最確値とその誤差 (Slide No.19~25 Text p.80~81) 誤差の伝播 (Slide No.26~32 Text
( 慣性抵抗 ) 速度の 2 乗に比例流体中を進む物体は前面にある流体を押しのけて進む. 物 aaa 体の後面には流体が付き従う ( 渦を巻いて ). 前面にある速度 0 の流体が後面に移動して速度 vとなったと考えてよい. この流体の質量は単位時間内に物体が押しのける体積に比例するので,v に比例
 空気抵抗があるときの自由落下 抵抗が速度に比例する場合 1. 絵を描く, 座標と情報, 記号を記入する x F0 v
空気抵抗があるときの自由落下 抵抗が速度に比例する場合 1. 絵を描く, 座標と情報, 記号を記入する x F0 v
数値計算で学ぶ物理学 4 放物運動と惑星運動 地上のように下向きに重力がはたらいているような場においては 物体を投げると放物運動をする 一方 中心星のまわりの重力場中では 惑星は 円 だ円 放物線または双曲線を描きながら運動する ここでは 放物運動と惑星運動を 運動方程式を導出したうえで 数値シミュ
 数値計算で学ぶ物理学 4 放物運動と惑星運動 地上のように下向きに重力がはたらいているような場においては 物体を投げると放物運動をする 一方 中心星のまわりの重力場中では 惑星は 円 だ円 放物線または双曲線を描きながら運動する ここでは 放物運動と惑星運動を 運動方程式を導出したうえで 数値シミュレーションによって計算してみる 4.1 放物運動一様な重力場における放物運動を考える 一般に質量の物体に作用する力をとすると運動方程式は
数値計算で学ぶ物理学 4 放物運動と惑星運動 地上のように下向きに重力がはたらいているような場においては 物体を投げると放物運動をする 一方 中心星のまわりの重力場中では 惑星は 円 だ円 放物線または双曲線を描きながら運動する ここでは 放物運動と惑星運動を 運動方程式を導出したうえで 数値シミュレーションによって計算してみる 4.1 放物運動一様な重力場における放物運動を考える 一般に質量の物体に作用する力をとすると運動方程式は
<4D F736F F F696E74202D2091E6824F82538FCD8CEB82E88C9F8F6F814592F990B382CC8CB4979D82BB82CC82505F D E95848D8682CC90B69
 第 章 誤り検出 訂正の原理 その ブロック符号とその復号 安達文幸 目次 誤り訂正符号化を用いる伝送系誤り検出符号誤り検出 訂正符号 7, ハミング符号, ハミング符号生成行列, パリティ検査行列の一般形符号の生成行列符号の生成行列とパリティ検査行列の関係符号の訂正能力符号多項式 安達 : コミュニケーション符号理論 安達 : コミュニケーション符号理論 誤り訂正符号化を用いる伝送系 伝送システム
第 章 誤り検出 訂正の原理 その ブロック符号とその復号 安達文幸 目次 誤り訂正符号化を用いる伝送系誤り検出符号誤り検出 訂正符号 7, ハミング符号, ハミング符号生成行列, パリティ検査行列の一般形符号の生成行列符号の生成行列とパリティ検査行列の関係符号の訂正能力符号多項式 安達 : コミュニケーション符号理論 安達 : コミュニケーション符号理論 誤り訂正符号化を用いる伝送系 伝送システム
Microsoft PowerPoint - Eigen.ppt [互換モード]
![Microsoft PowerPoint - Eigen.ppt [互換モード] Microsoft PowerPoint - Eigen.ppt [互換モード]](/thumbs/84/90658124.jpg) 固有値解析 中島研吾 東京大学情報基盤センター同大学院情報理工学系研究科数理情報学専攻数値解析 ( 科目番号 58) 行列の固有値問題 べき乗法 対称行列の固有値計算法 Eige Eige A 行列の固有値問題 標準固有値問題 (Stdrd Eigevle Problem を満足する と を求める : 固有値 (eigevle) : 固有ベクトル (eigevetor) 一般固有値問題 (Geerl
固有値解析 中島研吾 東京大学情報基盤センター同大学院情報理工学系研究科数理情報学専攻数値解析 ( 科目番号 58) 行列の固有値問題 べき乗法 対称行列の固有値計算法 Eige Eige A 行列の固有値問題 標準固有値問題 (Stdrd Eigevle Problem を満足する と を求める : 固有値 (eigevle) : 固有ベクトル (eigevetor) 一般固有値問題 (Geerl
偏微分方程式、連立1次方程式、乱数
 数値計算法 011/6/8 林田清 大阪大学大学院理学研究科 常微分方程式の応用例 1 Rutherford 散乱 ( 原子核同士の散乱 ; 金の薄膜に α 粒子をあてる ) 1 クーロン力 f= 4 0 r r r Ze y からf cos, si f f f y f f 粒子の 方向 y方向の速度と座標について dv Ze dvy Ze y, 3 3 dt 40m r dt 40m r d dy
数値計算法 011/6/8 林田清 大阪大学大学院理学研究科 常微分方程式の応用例 1 Rutherford 散乱 ( 原子核同士の散乱 ; 金の薄膜に α 粒子をあてる ) 1 クーロン力 f= 4 0 r r r Ze y からf cos, si f f f y f f 粒子の 方向 y方向の速度と座標について dv Ze dvy Ze y, 3 3 dt 40m r dt 40m r d dy
14 化学実験法 II( 吉村 ( 洋 mmol/l の半分だったから さんの測定値は くんの測定値の 4 倍の重みがあり 推定値 としては 0.68 mmol/l その標準偏差は mmol/l 程度ということになる 測定値を 特徴づけるパラメータ t を推定するこの手
 14 化学実験法 II( 吉村 ( 洋 014.6.1. 最小 乗法のはなし 014.6.1. 内容 最小 乗法のはなし...1 最小 乗法の考え方...1 最小 乗法によるパラメータの決定... パラメータの信頼区間...3 重みの異なるデータの取扱い...4 相関係数 決定係数 ( 最小 乗法を語るもう一つの立場...5 実験条件の誤差の影響...5 問題...6 最小 乗法の考え方 飲料水中のカルシウム濃度を
14 化学実験法 II( 吉村 ( 洋 014.6.1. 最小 乗法のはなし 014.6.1. 内容 最小 乗法のはなし...1 最小 乗法の考え方...1 最小 乗法によるパラメータの決定... パラメータの信頼区間...3 重みの異なるデータの取扱い...4 相関係数 決定係数 ( 最小 乗法を語るもう一つの立場...5 実験条件の誤差の影響...5 問題...6 最小 乗法の考え方 飲料水中のカルシウム濃度を
Microsoft PowerPoint - e-stat(OLS).pptx
 経済統計学 ( 補足 ) 最小二乗法について 担当 : 小塚匡文 2015 年 11 月 19 日 ( 改訂版 ) 神戸大学経済学部 2015 年度後期開講授業 補足 : 最小二乗法 ( 単回帰分析 ) 1.( 単純 ) 回帰分析とは? 標本サイズTの2 変数 ( ここではXとY) のデータが存在 YをXで説明する回帰方程式を推定するための方法 Y: 被説明変数 ( または従属変数 ) X: 説明変数
経済統計学 ( 補足 ) 最小二乗法について 担当 : 小塚匡文 2015 年 11 月 19 日 ( 改訂版 ) 神戸大学経済学部 2015 年度後期開講授業 補足 : 最小二乗法 ( 単回帰分析 ) 1.( 単純 ) 回帰分析とは? 標本サイズTの2 変数 ( ここではXとY) のデータが存在 YをXで説明する回帰方程式を推定するための方法 Y: 被説明変数 ( または従属変数 ) X: 説明変数
Microsoft PowerPoint - 10.pptx
 m u. 固有値とその応用 8/7/( 水 ). 固有値とその応用 固有値と固有ベクトル 行列による写像から固有ベクトルへ m m 行列 によって線形写像 f : R R が表せることを見てきた ここでは 次元平面の行列による写像を調べる とし 写像 f : を考える R R まず 単位ベクトルの像 u y y f : R R u u, u この事から 線形写像の性質を用いると 次の格子上の点全ての写像先が求まる
m u. 固有値とその応用 8/7/( 水 ). 固有値とその応用 固有値と固有ベクトル 行列による写像から固有ベクトルへ m m 行列 によって線形写像 f : R R が表せることを見てきた ここでは 次元平面の行列による写像を調べる とし 写像 f : を考える R R まず 単位ベクトルの像 u y y f : R R u u, u この事から 線形写像の性質を用いると 次の格子上の点全ての写像先が求まる
2 図微小要素の流体の流入出 方向の断面の流体の流入出の収支断面 Ⅰ から微小要素に流入出する流体の流量 Q 断面 Ⅰ は 以下のように定式化できる Q 断面 Ⅰ 流量 密度 流速 断面 Ⅰ の面積 微小要素の断面 Ⅰ から だけ移動した断面 Ⅱ を流入出する流体の流量 Q 断面 Ⅱ は以下のように
 3 章 Web に Link 解説 連続式 微分表示 の誘導.64 *4. 連続式連続式は ある領域の内部にある流体の質量の収支が その表面からの流入出の合計と等しくなることを定式化したものであり 流体における質量保存則を示したものである 2. 連続式 微分表示 の誘導図のような微小要素 コントロールボリューム の領域内の流体の増減と外部からの流体の流入出を考えることで定式化できる 微小要素 流入
3 章 Web に Link 解説 連続式 微分表示 の誘導.64 *4. 連続式連続式は ある領域の内部にある流体の質量の収支が その表面からの流入出の合計と等しくなることを定式化したものであり 流体における質量保存則を示したものである 2. 連続式 微分表示 の誘導図のような微小要素 コントロールボリューム の領域内の流体の増減と外部からの流体の流入出を考えることで定式化できる 微小要素 流入
応用数学A
 応用数学 A 米田 戸倉川月 7 限 1930~2100 西 5-109 V を :x 2 + y 2 + z 2 = 4 で囲まれる内部とする F = ye x xe y + ze z FdV = V e x e y e z F = = 2e z 2e z dv = 2e z 3 23 = 64π 3 e z y x z 4π V n Fd = 1 F nd 2 F nd 法線ベクトル n g x,
応用数学 A 米田 戸倉川月 7 限 1930~2100 西 5-109 V を :x 2 + y 2 + z 2 = 4 で囲まれる内部とする F = ye x xe y + ze z FdV = V e x e y e z F = = 2e z 2e z dv = 2e z 3 23 = 64π 3 e z y x z 4π V n Fd = 1 F nd 2 F nd 法線ベクトル n g x,
09.pptx
 講義内容 数値解析 第 9 回 5 年 6 月 7 日 水 理学部物理学科情報理学コース. 非線形方程式の数値解法. はじめに. 分法. 補間法.4 ニュートン法.4. 多変数問題への応用.4. ニュートン法の収束性. 連立 次方程式の解法. 序論と行列計算の基礎. ガウスの消去法. 重対角行列の場合の解法項目を変更しました.4 LU 分解法.5 特異値分解法.6 共役勾配法.7 反復法.7. ヤコビ法.7.
講義内容 数値解析 第 9 回 5 年 6 月 7 日 水 理学部物理学科情報理学コース. 非線形方程式の数値解法. はじめに. 分法. 補間法.4 ニュートン法.4. 多変数問題への応用.4. ニュートン法の収束性. 連立 次方程式の解法. 序論と行列計算の基礎. ガウスの消去法. 重対角行列の場合の解法項目を変更しました.4 LU 分解法.5 特異値分解法.6 共役勾配法.7 反復法.7. ヤコビ法.7.
vecrot
 1. ベクトル ベクトル : 方向を持つ量 ベクトルには 1 方向 2 大きさ ( 長さ ) という 2 つの属性がある ベクトルの例 : 物体の移動速度 移動量電場 磁場の強さ風速力トルクなど 2. ベクトルの表現 2.1 矢印で表現される 矢印の長さ : ベクトルの大きさ 矢印の向き : ベクトルの方向 2.2 2 個の点を用いて表現する 始点 () と終点 () を結ぶ半直線の向き : ベクトルの方向
1. ベクトル ベクトル : 方向を持つ量 ベクトルには 1 方向 2 大きさ ( 長さ ) という 2 つの属性がある ベクトルの例 : 物体の移動速度 移動量電場 磁場の強さ風速力トルクなど 2. ベクトルの表現 2.1 矢印で表現される 矢印の長さ : ベクトルの大きさ 矢印の向き : ベクトルの方向 2.2 2 個の点を用いて表現する 始点 () と終点 () を結ぶ半直線の向き : ベクトルの方向
を入れて,,, について解けば ( ) ( ) 得る. よって となるが ( / ( ) ( ) と無次元化している ), これを { N ( ) } { d} と表現して内部変位 と節点変位 { d} とを結びつける { } { ( ) ( ) } (.) (.) 節点での F と M は図. の
 第 章有限要素法 ( その ). 梁要素 有限要素法においては外力も境界条件も節点で考える. もちろん分布荷重は考慮でき るが, 要素上の分布荷重は適当に節点への等価は集中荷重として置き換える. こう考える と梁の曲げの方程式 (.8) において分布荷重無し (p()) の d d (.) である. この一般解は先に解いたように (.) となる. 梁の有限要素の長さを とすると, その両端, にて境界条件を導入して解い
第 章有限要素法 ( その ). 梁要素 有限要素法においては外力も境界条件も節点で考える. もちろん分布荷重は考慮でき るが, 要素上の分布荷重は適当に節点への等価は集中荷重として置き換える. こう考える と梁の曲げの方程式 (.8) において分布荷重無し (p()) の d d (.) である. この一般解は先に解いたように (.) となる. 梁の有限要素の長さを とすると, その両端, にて境界条件を導入して解い
<4D F736F F F696E74202D2095A8979D90948A CE394BC A2E707074>
 物理数学 1B( 後半部 ) 担当教員 : 山本貴博 講義内容 : ベクトル場における積分定理 第 1 回目講義 : 平面におけるグリーンの定理 ( 線積分 2 重積分 ) (12 月 11 日 ) 第 2 回目講義 : ガウスの定理 ( 面積分 体積分 ) (12 月 18 日 ) 第 3 回目講義 : ストークスの定理 ( 線積分 面積分 ) (1 月 15 日 ) 第 1 回目講義 : 平面におけるグリーンの定理
物理数学 1B( 後半部 ) 担当教員 : 山本貴博 講義内容 : ベクトル場における積分定理 第 1 回目講義 : 平面におけるグリーンの定理 ( 線積分 2 重積分 ) (12 月 11 日 ) 第 2 回目講義 : ガウスの定理 ( 面積分 体積分 ) (12 月 18 日 ) 第 3 回目講義 : ストークスの定理 ( 線積分 面積分 ) (1 月 15 日 ) 第 1 回目講義 : 平面におけるグリーンの定理
PowerPoint プレゼンテーション
 復習 ) 時系列のモデリング ~a. 離散時間モデル ~ y k + a 1 z 1 y k + + a na z n ay k = b 0 u k + b 1 z 1 u k + + b nb z n bu k y k = G z 1 u k = B(z 1 ) A(z 1 u k ) ARMA モデル A z 1 B z 1 = 1 + a 1 z 1 + + a na z n a = b 0
復習 ) 時系列のモデリング ~a. 離散時間モデル ~ y k + a 1 z 1 y k + + a na z n ay k = b 0 u k + b 1 z 1 u k + + b nb z n bu k y k = G z 1 u k = B(z 1 ) A(z 1 u k ) ARMA モデル A z 1 B z 1 = 1 + a 1 z 1 + + a na z n a = b 0
行列、ベクトル
 行列 (Mtri) と行列式 (Determinnt). 行列 (Mtri) の演算. 和 差 積.. 行列とは.. 行列の和差 ( 加減算 ).. 行列の積 ( 乗算 ). 転置行列 対称行列 正方行列. 単位行列. 行列式 (Determinnt) と逆行列. 行列式. 逆行列. 多元一次連立方程式のコンピュータによる解法. コンピュータによる逆行列の計算.. 定数項の異なる複数の方程式.. 逆行列の計算
行列 (Mtri) と行列式 (Determinnt). 行列 (Mtri) の演算. 和 差 積.. 行列とは.. 行列の和差 ( 加減算 ).. 行列の積 ( 乗算 ). 転置行列 対称行列 正方行列. 単位行列. 行列式 (Determinnt) と逆行列. 行列式. 逆行列. 多元一次連立方程式のコンピュータによる解法. コンピュータによる逆行列の計算.. 定数項の異なる複数の方程式.. 逆行列の計算
<4D F736F F F696E74202D208D E9197BF288CF68A4A B8CDD8AB B83685D>
 離散化手法とスキームの基礎 と選択法 007//6 宇宙航空研究開発機構情報 計算工学センター嶋英志 本講習の目的 基礎的な計算法の性質を述べ 各手法の持つ長所短所を理解することによって 手法の背景を理解した正しい選択に近づくこと クーラン数 風上差分 等の広い範囲の CFD 技術に共通の概念について その意味とイメージを把握すること 本講習の方針 様々な流体方程式の基礎となる移流方程式を用いて色々な計算法の特徴を計算例を示しながら解説する
離散化手法とスキームの基礎 と選択法 007//6 宇宙航空研究開発機構情報 計算工学センター嶋英志 本講習の目的 基礎的な計算法の性質を述べ 各手法の持つ長所短所を理解することによって 手法の背景を理解した正しい選択に近づくこと クーラン数 風上差分 等の広い範囲の CFD 技術に共通の概念について その意味とイメージを把握すること 本講習の方針 様々な流体方程式の基礎となる移流方程式を用いて色々な計算法の特徴を計算例を示しながら解説する
Microsoft PowerPoint - 第8章
 講義予定 案. 9/ 数値シミュレーションの手続き テキスト第 章. 9/ 9 偏微分方程式と解析解 テキスト第 章 3. 9/6 休講 4. 9/30 差分方程式とそのスキーム テキスト第 3 章 変換 テキスト第 4 章 5. 0/ 7 計算 テキスト第 5 章 連立一次方程式の解法 テキスト第 6 章 6. 0/ 流れ関数 ポテンシャルによる解法 テキスト第 7 章 7. 0/8 流速 圧力を用いた解法
講義予定 案. 9/ 数値シミュレーションの手続き テキスト第 章. 9/ 9 偏微分方程式と解析解 テキスト第 章 3. 9/6 休講 4. 9/30 差分方程式とそのスキーム テキスト第 3 章 変換 テキスト第 4 章 5. 0/ 7 計算 テキスト第 5 章 連立一次方程式の解法 テキスト第 6 章 6. 0/ 流れ関数 ポテンシャルによる解法 テキスト第 7 章 7. 0/8 流速 圧力を用いた解法
モデリングとは
 コンピュータグラフィックス基礎 第 5 回曲線 曲面の表現 ベジェ曲線 金森由博 学習の目標 滑らかな曲線を扱う方法を学習する パラメトリック曲線について理解する 広く一般的に使われているベジェ曲線を理解する 制御点を入力することで ベジェ曲線を描画するアプリケーションの開発を行えるようになる C++ 言語の便利な機能を使えるようになる 要素数が可変な配列としての std::vector の活用 計算機による曲線の表現
コンピュータグラフィックス基礎 第 5 回曲線 曲面の表現 ベジェ曲線 金森由博 学習の目標 滑らかな曲線を扱う方法を学習する パラメトリック曲線について理解する 広く一般的に使われているベジェ曲線を理解する 制御点を入力することで ベジェ曲線を描画するアプリケーションの開発を行えるようになる C++ 言語の便利な機能を使えるようになる 要素数が可変な配列としての std::vector の活用 計算機による曲線の表現
Microsoft Word - 1B2011.doc
 第 14 回モールの定理 ( 単純梁の場合 ) ( モールの定理とは何か?p.11) 例題 下記に示す単純梁の C 点のたわみ角 θ C と, たわみ δ C を求めよ ただし, 部材の曲げ 剛性は材軸に沿って一様で とする C D kn B 1.5m 0.5m 1.0m 解答 1 曲げモーメント図を描く,B 点の反力を求める kn kn 4 kn 曲げモーメント図を描く knm 先に得られた曲げモーメントの値を
第 14 回モールの定理 ( 単純梁の場合 ) ( モールの定理とは何か?p.11) 例題 下記に示す単純梁の C 点のたわみ角 θ C と, たわみ δ C を求めよ ただし, 部材の曲げ 剛性は材軸に沿って一様で とする C D kn B 1.5m 0.5m 1.0m 解答 1 曲げモーメント図を描く,B 点の反力を求める kn kn 4 kn 曲げモーメント図を描く knm 先に得られた曲げモーメントの値を
Microsoft PowerPoint - 9.pptx
 9/7/8( 水 9. 線形写像 ここでは 行列の積によって 写像を定義できることをみていく また 行列の積によって定義される写像の性質を調べていく 拡大とスカラー倍 行列演算と写像 ( 次変換 拡大後 k 倍 k 倍 k 倍拡大の関係は スカラー倍を用いて次のように表現できる p = (, ' = k ' 拡大前 p ' = ( ', ' = ( k, k 拡大 4 拡大と行列の積 拡大後 k 倍
9/7/8( 水 9. 線形写像 ここでは 行列の積によって 写像を定義できることをみていく また 行列の積によって定義される写像の性質を調べていく 拡大とスカラー倍 行列演算と写像 ( 次変換 拡大後 k 倍 k 倍 k 倍拡大の関係は スカラー倍を用いて次のように表現できる p = (, ' = k ' 拡大前 p ' = ( ', ' = ( k, k 拡大 4 拡大と行列の積 拡大後 k 倍
学習指導要領
 (1) 数と式 学習指導要領 数と式 (1) 式の計算二次の乗法公式及び因数分解の公式の理解を深め 式を多面的にみたり目的に応じて式を適切に変形したりすること 東京都立町田高等学校学力スタンダード 整式の加法 減法 乗法展開の公式を利用できる 式を1 つの文字におき換えることによって, 式の計算を簡略化することができる 式の形の特徴に着目して変形し, 展開の公式が適用できるようにすることができる 因数分解因数分解の公式を利用できる
(1) 数と式 学習指導要領 数と式 (1) 式の計算二次の乗法公式及び因数分解の公式の理解を深め 式を多面的にみたり目的に応じて式を適切に変形したりすること 東京都立町田高等学校学力スタンダード 整式の加法 減法 乗法展開の公式を利用できる 式を1 つの文字におき換えることによって, 式の計算を簡略化することができる 式の形の特徴に着目して変形し, 展開の公式が適用できるようにすることができる 因数分解因数分解の公式を利用できる
Microsoft PowerPoint - 三次元座標測定 ppt
 冗長座標測定機 ()( 三次元座標計測 ( 第 9 回 ) 5 年度大学院講義 6 年 月 7 日 冗長性を持つ 次元座標測定機 次元 辺測量 : 冗長性を出すために つのレーザトラッカを配置し, キャッツアイまでの距離から座標を測定する つのカメラ ( 次元的なカメラ ) とレーザスキャナ : つの角度測定システムによる座標測定 つの回転関節による 次元 自由度多関節機構 高増潔東京大学工学系研究科精密機械工学専攻
冗長座標測定機 ()( 三次元座標計測 ( 第 9 回 ) 5 年度大学院講義 6 年 月 7 日 冗長性を持つ 次元座標測定機 次元 辺測量 : 冗長性を出すために つのレーザトラッカを配置し, キャッツアイまでの距離から座標を測定する つのカメラ ( 次元的なカメラ ) とレーザスキャナ : つの角度測定システムによる座標測定 つの回転関節による 次元 自由度多関節機構 高増潔東京大学工学系研究科精密機械工学専攻
DVIOUT
 最適レギュレータ 松尾研究室資料 第 最適レギュレータ 節時不変型無限時間最適レギュレータ 状態フィードバックの可能な場合の無限時間問題における最適レギュレータについて確定系について説明する. ここで, レギュレータとは状態量をゼロにするようなコントローラのことである. なぜ, 無限時間問題のみを述べるかという理由は以下のとおりである. 有限時間の最適レギュレータ問題の場合の最適フィードバックゲインは微分方程式の解から構成される時間関数として表現される.
最適レギュレータ 松尾研究室資料 第 最適レギュレータ 節時不変型無限時間最適レギュレータ 状態フィードバックの可能な場合の無限時間問題における最適レギュレータについて確定系について説明する. ここで, レギュレータとは状態量をゼロにするようなコントローラのことである. なぜ, 無限時間問題のみを述べるかという理由は以下のとおりである. 有限時間の最適レギュレータ問題の場合の最適フィードバックゲインは微分方程式の解から構成される時間関数として表現される.
計算機シミュレーション
 . 運動方程式の数値解法.. ニュートン方程式の近似速度は, 位置座標 の時間微分で, d と定義されます. これを成分で書くと, d d li li とかけます. 本来は が の極限をとらなければいけませんが, 有限の小さな値とすると 秒後の位置座標は速度を用いて, と近似できます. 同様にして, 加速度は, 速度 の時間微分で, d と定義されます. これを成分で書くと, d d li li とかけます.
. 運動方程式の数値解法.. ニュートン方程式の近似速度は, 位置座標 の時間微分で, d と定義されます. これを成分で書くと, d d li li とかけます. 本来は が の極限をとらなければいけませんが, 有限の小さな値とすると 秒後の位置座標は速度を用いて, と近似できます. 同様にして, 加速度は, 速度 の時間微分で, d と定義されます. これを成分で書くと, d d li li とかけます.
学習指導要領
 (1 ) 数と式 ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 自然数 整数 有理数 無理数の包含関係など 実 数の構成を理解する ( 例 ) 次の空欄に適当な言葉をいれて, 数の集合を表しなさい 実数の絶対値が実数と対応する点と原点との距離で あることを理解する ( 例 ) 次の値を求めよ (1) () 6 置き換えなどを利用して 三項の無理数の乗法の計
(1 ) 数と式 ア数と集合 ( ア ) 実数数を実数まで拡張する意義を理解し 簡単な無理数の四則計算をすること 自然数 整数 有理数 無理数の包含関係など 実 数の構成を理解する ( 例 ) 次の空欄に適当な言葉をいれて, 数の集合を表しなさい 実数の絶対値が実数と対応する点と原点との距離で あることを理解する ( 例 ) 次の値を求めよ (1) () 6 置き換えなどを利用して 三項の無理数の乗法の計
構造力学Ⅰ第12回
 第 回材の座屈 (0 章 ) p.5~ ( 復習 ) モールの定理 ( 手順 ) 座屈とは 荷重により梁に生じた曲げモーメントをで除して仮想荷重と考える 座屈荷重 偏心荷重 ( 曲げと軸力 ) 断面の核 この仮想荷重に対するある点でのせん断力 たわみ角に相当する曲げモーメント たわみに相当する ( 例 ) 単純梁の支点のたわみ角 : は 図 を仮想荷重と考えたときの 点の支点反力 B は 図 を仮想荷重と考えたときのB
第 回材の座屈 (0 章 ) p.5~ ( 復習 ) モールの定理 ( 手順 ) 座屈とは 荷重により梁に生じた曲げモーメントをで除して仮想荷重と考える 座屈荷重 偏心荷重 ( 曲げと軸力 ) 断面の核 この仮想荷重に対するある点でのせん断力 たわみ角に相当する曲げモーメント たわみに相当する ( 例 ) 単純梁の支点のたわみ角 : は 図 を仮想荷重と考えたときの 点の支点反力 B は 図 を仮想荷重と考えたときのB
Microsoft PowerPoint - mp11-02.pptx
 数理計画法第 2 回 塩浦昭義情報科学研究科准教授 shioura@dais.is.tohoku.ac.jp http://www.dais.is.tohoku.ac.jp/~shioura/teaching 前回の復習 数理計画とは? 数理計画 ( 復習 ) 数理計画問題とは? 狭義には : 数理 ( 数学 ) を使って計画を立てるための問題 広義には : 与えられた評価尺度に関して最も良い解を求める問題
数理計画法第 2 回 塩浦昭義情報科学研究科准教授 shioura@dais.is.tohoku.ac.jp http://www.dais.is.tohoku.ac.jp/~shioura/teaching 前回の復習 数理計画とは? 数理計画 ( 復習 ) 数理計画問題とは? 狭義には : 数理 ( 数学 ) を使って計画を立てるための問題 広義には : 与えられた評価尺度に関して最も良い解を求める問題
"éı”ç·ıå½¢ 微勃挹稉弑
 == 1 階線形微分方程式 == 次の形の常微分方程式を1 階線形常微分方程式といいます. '+P()=Q() (1) 方程式 (1) の右辺 : Q() を 0 とおいてできる同次方程式 ( この同次方程式は, 変数分離形になり比較的容易に解けます ) '+P()=0 () の1つの解を とすると, 方程式 (1) の一般解は =( Q() +C) (3) で求められます. 参考書には 上記の の代わりに,
== 1 階線形微分方程式 == 次の形の常微分方程式を1 階線形常微分方程式といいます. '+P()=Q() (1) 方程式 (1) の右辺 : Q() を 0 とおいてできる同次方程式 ( この同次方程式は, 変数分離形になり比較的容易に解けます ) '+P()=0 () の1つの解を とすると, 方程式 (1) の一般解は =( Q() +C) (3) で求められます. 参考書には 上記の の代わりに,
1 対 1 対応の演習例題を解いてみた 微分法とその応用 例題 1 極限 微分係数の定義 (2) 関数 f ( x) は任意の実数 x について微分可能なのは明らか f ( 1, f ( 1) ) と ( 1 + h, f ( 1 + h)
 微分法とその応用 例題 1 極限 微分係数の定義 () 関数 ( x) は任意の実数 x について微分可能なのは明らか ( 1, ( 1) ) と ( 1 + h, ( 1 + h) ) の傾き= ( 1 + h ) - ( 1 ) ( 1 + ) - ( 1) = ( 1 + h) - 1 h ( 1) = lim h ( 1 + h) - ( 1) h ( 1, ( 1) ) と ( 1 - h,
微分法とその応用 例題 1 極限 微分係数の定義 () 関数 ( x) は任意の実数 x について微分可能なのは明らか ( 1, ( 1) ) と ( 1 + h, ( 1 + h) ) の傾き= ( 1 + h ) - ( 1 ) ( 1 + ) - ( 1) = ( 1 + h) - 1 h ( 1) = lim h ( 1 + h) - ( 1) h ( 1, ( 1) ) と ( 1 - h,
memo
 数理情報工学特論第一 機械学習とデータマイニング 4 章 : 教師なし学習 3 かしまひさし 鹿島久嗣 ( 数理 6 研 ) kashima@mist.i.~ DEPARTMENT OF MATHEMATICAL INFORMATICS 1 グラフィカルモデルについて学びます グラフィカルモデル グラフィカルラッソ グラフィカルラッソの推定アルゴリズム 2 グラフィカルモデル 3 教師なし学習の主要タスクは
数理情報工学特論第一 機械学習とデータマイニング 4 章 : 教師なし学習 3 かしまひさし 鹿島久嗣 ( 数理 6 研 ) kashima@mist.i.~ DEPARTMENT OF MATHEMATICAL INFORMATICS 1 グラフィカルモデルについて学びます グラフィカルモデル グラフィカルラッソ グラフィカルラッソの推定アルゴリズム 2 グラフィカルモデル 3 教師なし学習の主要タスクは
8. 自由曲線と曲面の概要 陽関数 陰関数 f x f x x y y y f f x y z g x y z パラメータ表現された 次元曲線 パラメータ表現は xyx 毎のパラメータによる陽関数表現 形状普遍性 座標独立性 曲線上の点を直接に計算可能 多価の曲線も表現可能 gx 低次の多項式は 計
 8. 自由曲線 曲面. 概論. ベジエ曲線 曲面. ベジエ曲線 曲面の数学. OeGLによる実行. URS. スプライン関数. スプライン曲線 曲面. URS 曲線 曲面 4. OeGLによる実行 8. 自由曲線と曲面の概要 陽関数 陰関数 f x f x x y y y f f x y z g x y z パラメータ表現された 次元曲線 パラメータ表現は xyx 毎のパラメータによる陽関数表現 形状普遍性
8. 自由曲線 曲面. 概論. ベジエ曲線 曲面. ベジエ曲線 曲面の数学. OeGLによる実行. URS. スプライン関数. スプライン曲線 曲面. URS 曲線 曲面 4. OeGLによる実行 8. 自由曲線と曲面の概要 陽関数 陰関数 f x f x x y y y f f x y z g x y z パラメータ表現された 次元曲線 パラメータ表現は xyx 毎のパラメータによる陽関数表現 形状普遍性
代数 幾何 < ベクトル > 1 ベクトルの演算 和 差 実数倍については 文字の計算と同様 2 ベクトルの成分表示 平面ベクトル : a x e y e x, ) ( 1 y1 空間ベクトル : a x e y e z e x, y, ) ( 1 1 z1
 代数 幾何 < ベクトル > ベクトルの演算 和 差 実数倍については 文字の計算と同様 ベクトルの成分表示 平面ベクトル :, 空間ベクトル : z,, z 成分での計算ができるようにすること ベクトルの内積 : os 平面ベクトル :,, 空間ベクトル :,,,, z z zz 4 ベクトルの大きさ 平面上 : 空間上 : z は 良く用いられる 5 m: に分ける点 : m m 図形への応用
代数 幾何 < ベクトル > ベクトルの演算 和 差 実数倍については 文字の計算と同様 ベクトルの成分表示 平面ベクトル :, 空間ベクトル : z,, z 成分での計算ができるようにすること ベクトルの内積 : os 平面ベクトル :,, 空間ベクトル :,,,, z z zz 4 ベクトルの大きさ 平面上 : 空間上 : z は 良く用いられる 5 m: に分ける点 : m m 図形への応用
<4D F736F F D20824F B834E835882CC92E8979D814690FC90CF95AA82C696CA90CF95AA2E646F63>
 1/10 平成 23 年 6 月 1 日午後 4 時 33 分 07 ストークスの定理 : 線積分と面積分 07 ストークスの定理 : 線積分と面積分 ストークスの定理はガウスの定理とともに 非常に重要な定理であり 線積分と面積分の関係を表します つまり ガウスの定理 : 面積分と体積分 ( 体積を囲む閉じた面 = 表面 ) の関係 ストークスの定理 : 線積分と面積分 ( 面積を囲む外周の線 )
1/10 平成 23 年 6 月 1 日午後 4 時 33 分 07 ストークスの定理 : 線積分と面積分 07 ストークスの定理 : 線積分と面積分 ストークスの定理はガウスの定理とともに 非常に重要な定理であり 線積分と面積分の関係を表します つまり ガウスの定理 : 面積分と体積分 ( 体積を囲む閉じた面 = 表面 ) の関係 ストークスの定理 : 線積分と面積分 ( 面積を囲む外周の線 )
スライド 1
 暫定版修正 加筆の可能性あり ( 付録 球面波 回折 (. グリーンの定理. キルヒホッフの積分定理 3. ホイヘンスの原理 4. キルヒホッフの回折公式 5. ゾンマーフェルトの放射条件 6. 補足 付録 (90~904 のアプローチ : 回折 (diffaction までの道標. 球面波 (pheical wave のみ対象 : スカラー表示. 虚数単位 i を使用する 3. お詫び : 自己流かつ説明が飛躍する場面があります
暫定版修正 加筆の可能性あり ( 付録 球面波 回折 (. グリーンの定理. キルヒホッフの積分定理 3. ホイヘンスの原理 4. キルヒホッフの回折公式 5. ゾンマーフェルトの放射条件 6. 補足 付録 (90~904 のアプローチ : 回折 (diffaction までの道標. 球面波 (pheical wave のみ対象 : スカラー表示. 虚数単位 i を使用する 3. お詫び : 自己流かつ説明が飛躍する場面があります
NAPRA
 研究の動機 圧縮応力下の破壊現象 主要な亀裂の破壊に支配される引張応力下の破壊現象と異なり, 亀裂群の破壊パターンが多様 物理亀裂の進展条件 数理多様な破壊パターン 理論解析と数値解析 現状理論解析が主, 数値解析を従 将来 数値解析が主, 理論解析を従 数値解析を前提とした数理問題の設定が必要 背景 解析が困難な破壊現象 亀裂の三次元的進展 圧縮応力下での破壊 破壊問題を解くために FEM に導入される技巧
研究の動機 圧縮応力下の破壊現象 主要な亀裂の破壊に支配される引張応力下の破壊現象と異なり, 亀裂群の破壊パターンが多様 物理亀裂の進展条件 数理多様な破壊パターン 理論解析と数値解析 現状理論解析が主, 数値解析を従 将来 数値解析が主, 理論解析を従 数値解析を前提とした数理問題の設定が必要 背景 解析が困難な破壊現象 亀裂の三次元的進展 圧縮応力下での破壊 破壊問題を解くために FEM に導入される技巧
スライド 1
 データ解析特論第 10 回 ( 全 15 回 ) 2012 年 12 月 11 日 ( 火 ) 情報エレクトロニクス専攻横田孝義 1 終了 11/13 11/20 重回帰分析をしばらくやります 12/4 12/11 12/18 2 前回から回帰分析について学習しています 3 ( 単 ) 回帰分析 単回帰分析では一つの従属変数 ( 目的変数 ) を 一つの独立変数 ( 説明変数 ) で予測する事を考える
データ解析特論第 10 回 ( 全 15 回 ) 2012 年 12 月 11 日 ( 火 ) 情報エレクトロニクス専攻横田孝義 1 終了 11/13 11/20 重回帰分析をしばらくやります 12/4 12/11 12/18 2 前回から回帰分析について学習しています 3 ( 単 ) 回帰分析 単回帰分析では一つの従属変数 ( 目的変数 ) を 一つの独立変数 ( 説明変数 ) で予測する事を考える
Microsoft Word - 町田・全 H30学力スタ 別紙1 1年 数学Ⅰ.doc
 (1) 数と式 学習指導要領 都立町田高校 学力スタンダード ア 数と集合 ( ア ) 実数 根号を含む式の計算 数を実数まで拡張する意義を理解し 簡単な 循環小数を表す記号を用いて, 分数を循環小数で表 無理数の四則計算をすること すことができる 今まで学習してきた数の体系について整理し, 考察 しようとする 絶対値の意味と記号表示を理解している 根号を含む式の加法, 減法, 乗法の計算ができる
(1) 数と式 学習指導要領 都立町田高校 学力スタンダード ア 数と集合 ( ア ) 実数 根号を含む式の計算 数を実数まで拡張する意義を理解し 簡単な 循環小数を表す記号を用いて, 分数を循環小数で表 無理数の四則計算をすること すことができる 今まで学習してきた数の体系について整理し, 考察 しようとする 絶対値の意味と記号表示を理解している 根号を含む式の加法, 減法, 乗法の計算ができる
Microsoft PowerPoint - 発表II-3原稿r02.ppt [互換モード]
![Microsoft PowerPoint - 発表II-3原稿r02.ppt [互換モード] Microsoft PowerPoint - 発表II-3原稿r02.ppt [互換モード]](/thumbs/91/105561911.jpg) 地震時の原子力発電所燃料プールからの溢水量解析プログラム 地球工学研究所田中伸和豊田幸宏 Central Research Institute of Electric Power Industry 1 1. はじめに ( その 1) 2003 年十勝沖地震では 震源から離れた苫小牧地区の石油タンクに スロッシング ( 液面揺動 ) による火災被害が生じた 2007 年中越沖地震では 原子力発電所内の燃料プールからの溢水があり
地震時の原子力発電所燃料プールからの溢水量解析プログラム 地球工学研究所田中伸和豊田幸宏 Central Research Institute of Electric Power Industry 1 1. はじめに ( その 1) 2003 年十勝沖地震では 震源から離れた苫小牧地区の石油タンクに スロッシング ( 液面揺動 ) による火災被害が生じた 2007 年中越沖地震では 原子力発電所内の燃料プールからの溢水があり
