応用音響学 第9回 音場の境界値積分表現
|
|
|
- ゆゆこ わしあし
- 2 years ago
- Views:
Transcription
1 応用音響学第 9 回 小山翔一 東京大学大学院情報理工学系研究科システム情報学専攻 2021/6/11 小山翔一 (UTokyo) 応用音響学第 9 回 2021/6/11 1 / 62
2 講義スケジュール S セメスター金曜 2 限 オンライン 日程 4/9 第 1 回 4/16 第 2 回 4/23 第 3 回 4/30 第 4 回 5/7 第 5 回 5/14 第 6 回 猿渡先生 5/21 第 7 回 5/28 休講 6/4 第 8 回 6/11 第 9 回 6/18 第 10 回 6/25 休講 7/2 第 11 回 7/9 第 12 回 小山 小山翔一 (UTokyo) 応用音響学第 9 回 2021/6/11 2 / 62
3 講義目的 講義前半 ( 猿渡先生担当 ) 音声分析, 音声符号化, 音声認識, 音声合成, 音響信号処理などに関連する基礎知識について講義する 応用として, 携帯電話や MP3 などの音声音楽情報圧縮技術や音声認識技術 音声合成システムなどがある 統計的信号処理の基礎, スペクトル解析, パターン認識, 確率モデル, 統計学習, 最適解探策などの基本概念とアルゴリズムを理解し, これらの技術の基礎になる知識と概念の習得を目指す 講義後半 ( 小山担当 ) 音響現象の数理的なモデリング方法を理解することを目的とし, 音波の伝播, 反射, 回折, 散乱などの現象を数学的に記述するための基礎事項について講義する 応用として, 音源位置の推定や音場の可視化, 音の VR/AR や騒音 振動制御, 音響数値シミュレーションなどがある これらの基本概念を理解することで, 様々な波動場の計測 制御技術の基礎となる知識の習得を目指す 小山翔一 (UTokyo) 応用音響学第 9 回 2021/6/11 3 / 62
4 講義後半の概要 講義内容 ( 予定 ) 5/21: 音波の伝播 6/4: 音響管 自由空間中の音波 6/11: 6/18: フーリエ音響学 (1) 7/2: フーリエ音響学 (2) 7/9: 室内音響学と音響数値シミュレーション参考文献 安田仁彦, 機械音響学, コロナ社, E. G. Williams, Fourier Acoustics: Sound Radiation and Nearfield Acoustical Holography, Academic Press, 小山翔一 (UTokyo) 応用音響学第 9 回 2021/6/11 4 / 62
5 講義資料と成績評価 講義資料 ITC-LMS に前日までにアップロード予定 あるいはシステム 1 研のウェブサイトからもたどれます成績評価 レポート or オンライン試験 (7/30) 小山翔一 (UTokyo) 応用音響学第 9 回 2021/6/11 5 / 62
6 本日の目次 1 境界値積分表現とその応用 Green 関数とその性質 Kirchhoff Helmholtz 積分方程式境界条件を与えた場合の Green 関数 Single layer potential による音場の積分表現 小山翔一 (UTokyo) 応用音響学第 9 回 2021/6/11 6 / 62
7 境界値積分表現とその応用 本日の目次 1 境界値積分表現とその応用 Green 関数とその性質 Kirchhoff Helmholtz 積分方程式境界条件を与えた場合の Green 関数 Single layer potential による音場の積分表現 小山翔一 (UTokyo) 応用音響学第 9 回 2021/6/11 7 / 62
8 境界値積分表現とその応用 とは? ある境界面上の値から, その内部あるいは外部への伝播を記述する積分表現 音源のパラメータを陽に与えることなく音場を記述できる 基本的には音源が境界面の内部あるいは外部のみに含まれると仮定し, 音源の存在しない空間への伝播 ( 順問題 ) を定式化する 小山翔一 (UTokyo) 応用音響学第 9 回 2021/6/11 8 / 62
9 境界値積分表現とその応用 の応用例 音響数値シミュレーション 波動場の数値解析, e.g., 境界要素法 (Boundary element method) 音響ホログラフィ / 音場再構成 ( 特に伝播の逆方向に関して ) 複数の観測値から音圧分布を推定音場の合成 / 制御 複数のスピーカを用いて所望の音場を合成 / 制御 Figure: application/hologram.htm より 小山翔一 (UTokyo) 応用音響学第 9 回 2021/6/11 9 / 62
10 Green 関数とその性質 本日の目次 1 境界値積分表現とその応用 Green 関数とその性質 Kirchhoff Helmholtz 積分方程式境界条件を与えた場合の Green 関数 Single layer potential による音場の積分表現 小山翔一 (UTokyo) 応用音響学第 9 回 2021/6/11 10 / 62
11 Green 関数とその性質 Green 関数 Green 関数は, 角周波数 ω の定常な場において, ある点 r に与えた単位作用のある点 r での場の量 ( 音圧や粒子速度 ) に与える影響を, 2 つの点の関数 G(r r ) として記述する 重ね合わせの原理により物理系に対する作用を細分化して考えるために,Green 関数を求めることは有用 Helmholtz 方程式に関する自由空間 Green 関数 G(r r ) は, を満たし, 2 G(r r ) + k 2 G(r r ) = δ(r r ) G(r r ) = ejk r r 4π r r 小山翔一 (UTokyo) 応用音響学第 9 回 2021/6/11 11 / 62
12 Green 関数とその性質 Green 関数 自由空間 Green 関数では位置 r = r の点音源である δ 関数のみを与えたが, 一般に Green 関数は, 音源に加えて境界条件や ( 波動方程式の場合 ) 初期条件を与えることで定まる よく出てくる境界条件 Neumann 境界条件は, 境界面上での音圧の ( 外向き ) 法線方向微分 p/ n を 0 とする Dirichlet 境界条件は, 境界面上での音圧 p を 0 とするこれらを満たす Green 関数を Neumann 型,Dirichlet 型 Green 関数と呼ぶ Robin 境界条件は,Neumann 境界条件と Dirichlet 境界条件の組み合わせ ap + b p n = g ここで a,b は定数であり,g は境界面上で定義される関数 さらに一般化して a,b を関数とする場合もある 小山翔一 (UTokyo) 応用音響学第 9 回 2021/6/11 12 / 62
13 Green 関数とその性質 Green 関数の相反性 Green 関数 G(r r ) が, ( 2 + k 2 )G(r r ) = δ(r r ) を満たし, 境界面において以下を満たすとする ag(r r ) + b G(r r ) n = 0 このとき,Green 関数は相反性 (reciprocity) を持つ G(r r ) = G(r r) 小山翔一 (UTokyo) 応用音響学第 9 回 2021/6/11 13 / 62
14 Green 関数とその性質 Green 関数の相反性 証明は以下の Green の ( 第 2) 定理を用いる Green の ( 第 2) 定理 ある領域とその境界面をそれぞれ V,S とし,V 内で 1 階および 2 階微分が連続かつ有界な関数 Φ(r),Ψ(r) に対して, 以下が成り立つ V ( Φ 2 Ψ Ψ 2 Φ ) dv = S ( Φ Ψ ) n Ψ Φ ds n 小山翔一 (UTokyo) 応用音響学第 9 回 2021/6/11 14 / 62
15 Green 関数とその性質 Green 関数の相反性 Φ = G(r r ),Ψ = G(r r ) として, ( ) G(r r ) G(r r ) G(r r ) G(r r ) ds S n n ( = G(r r ) 2 G(r r ) G(r r ) 2 G(r r ) ) dv V ( = G(r r )δ(r r ) G(r r )δ(r r ) ) dv V = G(r r ) G(r r ) さらに境界条件より, 第 1 式は 0 になることから, G(r r ) = G(r r ) 小山翔一 (UTokyo) 応用音響学第 9 回 2021/6/11 15 / 62
16 Green 関数とその性質 Green 関数の相反性 Green 関数の相反性 (reciprocity) G(r r ) = G(r r) つまり, 音源位置と評価位置を入れ替えても Green 関数は等しい 小山翔一 (UTokyo) 応用音響学第 9 回 2021/6/11 16 / 62
17 Kirchhoff Helmholtz 積分方程式 本日の目次 1 境界値積分表現とその応用 Green 関数とその性質 Kirchhoff Helmholtz 積分方程式境界条件を与えた場合の Green 関数 Single layer potential による音場の積分表現 小山翔一 (UTokyo) 応用音響学第 9 回 2021/6/11 17 / 62
18 Kirchhoff Helmholtz 積分方程式 Huygens の原理 波面の伝播は, ある瞬間の波面のそれぞれの点から, 球面状の二次波 ( 素元波 ) が出ていると考える 波動の回折現象を説明するために導入された Huygens の原理をより数学的に記述するには? Figure: ホイヘンス = フレネルの原理より 小山翔一 (UTokyo) 応用音響学第 9 回 2021/6/11 18 / 62
19 Kirchhoff Helmholtz 積分方程式 Helmholtz 方程式の境界値積分表現 境界面と境界条件が決まると,Helmholtz 方程式の解は Green 関数を用いた積分として表される Green の定理をもう一度思い出すと, ( Φ 2 Ψ Ψ 2 Φ ) ( dv = Φ Ψ ) n Ψ Φ ds n V これら 2 つの関数 Φ(r) と Ψ(r) が斉次 Helmholtz 方程式を満たすとする 2 Φ + k 2 Φ = 0, 2 Ψ + k 2 Ψ = 0 このとき,Green の定理の左辺の被積分関数は 0 となるので, ( Φ Ψ ) n Ψ Φ ds = 0 n S 上式が Helmholtz 方程式の境界値積分表現を導くための基礎となる 小山翔一 (UTokyo) 応用音響学第 9 回 2021/6/11 19 / 62 S
20 Kirchhoff Helmholtz 積分方程式 境界値積分表現における内部問題と外部問題 2 つの境界値積分表現内部問題 ある領域 Ω の境界面 Ω から, 領域内部への音場を記述 音源は Ω の外側に存在 外部問題 ある領域 Ω の境界面 Ω から, 領域外部への音場を記述 音源は Ω の内側に存在 ( 放射音場 ) 小山翔一 (UTokyo) 応用音響学第 9 回 2021/6/11 20 / 62
21 Kirchhoff Helmholtz 積分方程式 内部問題における Kirchhoff Helmholtz 積分方程式 内部問題における Helmholtz 方程式の境界値積分表現を考える Green の定理において,Ψ が領域 Ω 内の位置 r = r に特異点を持ち,Φ は連続である場合を考える 2 Ψ + k 2 Ψ = δ(r r ) ここで Ψ には (Sommerfeld の放射条件を満たすことを除いて ) 境界条件は存在しない 一般解は, 特殊解 Ψ p と斉次解 Ψ h との和として書ける Ψ = Ψ p + Ψ h 特殊解 Ψ p は, 自由空間 Green 関数 G(r r ) に等しいことから, Ψ p = G(r r ) = ejk r r 4π r r 小山翔一 (UTokyo) 応用音響学第 9 回 2021/6/11 21 / 62
22 Kirchhoff Helmholtz 積分方程式 内部問題における Kirchhoff Helmholtz 積分方程式 Ψ h = 0 つまり Ψ = Ψ p = G(r r ) となるように, 領域 Ω が特異点を取り除くように変形することを考える 図のように, 境界面 Ω を特異点を囲う半径 ϵ の微小球面 S i と外部表面 S o の結合による形とすると, この領域で Ψ と Φ は連続となることから,Green の定理が成り立つ S o ( Φ G(r r ) n + lim ϵ 0 S i G(r r ) Φ n ) ds o ( Φ G(r r ) G(r r ) Φ n n ) ds i = 0 小山翔一 (UTokyo) 応用音響学第 9 回 2021/6/11 22 / 62
23 Kirchhoff Helmholtz 積分方程式 内部問題における Kirchhoff Helmholtz 積分方程式 微小球上の積分である第 2 項を考える lim ϵ 0 S i ( Φ G(r r ) G(r r ) Φ n n ) ds i 第 2 項は / n = / ϵ,g(r r ) = e jkϵ /4πϵ, ds i = ϵ 2 sin θdθdϕ より, ( lim G(r r ) Φ ) ds i ϵ 0 n Φ(r) = lim ϵ 0 ϵ G(r r )ϵ 2 sin θdθdϕ r=r = lim ϵ Φ(r) ϵ 0 ϵ = 0 r=r Φ(r) は r = r まわりで連続であることに注意 小山翔一 (UTokyo) 応用音響学第 9 回 2021/6/11 23 / 62
24 Kirchhoff Helmholtz 積分方程式 内部問題における Kirchhoff Helmholtz 積分方程式 第 1 項は, sin θdθdϕ = 4π より, ( ) lim Φ G(r r ) G(r r ) ds i = lim Φ(r) ϵ 0 S i n ϵ 0 r=r n ϵ2 sin θdθdϕ = Φ(r ) ここで, 以下の近似を用いた G(r r ) n = ejkϵ /ϵ ϵ = ejkϵ ejkϵ (jk 1/ϵ) 4πϵ 4πϵ 2 以上により,r Ω\ Ω において, Φ(r ) = Ω ( G(r r ) Φ n ) Φ G(r r n ) dr 小山翔一 (UTokyo) 応用音響学第 9 回 2021/6/11 24 / 62
25 Kirchhoff Helmholtz 積分方程式 内部問題における Kirchhoff Helmholtz 積分方程式 評価点 r が境界面上にある場合 (r Ω), 微小球 S i 上の積分は 1/2 が掛けられた形となるので, ( 1 2 Φ(r ) = G(r r ) Φ ) Ω n ) Φ G(r r dr n 評価点 r が領域 Ω の外にある場合 (r R 3 \Ω), 特異点が存在しないため Green の定理が Ω 内のあらゆる位置で成り立つので, ( 0 = G(r r ) Φ ) n ) Φ G(r r dr n Ω 小山翔一 (UTokyo) 応用音響学第 9 回 2021/6/11 25 / 62
26 Kirchhoff Helmholtz 積分方程式 内部問題における Kirchhoff Helmholtz 積分方程式 以上により,Helmholtz 方程式の境界値積分表現として, 内部問題における Kirchhoff Helmholtz 積分方程式が得られた 内部問題における Kirchhoff Helmholtz 積分方程式 ある音源を含まない領域 Ω 内部の位置 r Ω\ Ω における音圧 p(r) は, 境界面 Ω 上の積分方程式によって以下のように得られる ( ) p(r) = G(r r ) p(r ) n p(r ) G(r r ) n dr Ω 小山翔一 (UTokyo) 応用音響学第 9 回 2021/6/11 26 / 62
27 Kirchhoff Helmholtz 積分方程式 内部問題における Kirchhoff Helmholtz 積分方程式 以上により,Helmholtz 方程式の境界値積分表現として, 内部問題における Kirchhoff Helmholtz 積分方程式が得られた 内部問題における Kirchhoff Helmholtz 積分方程式 ある音源を含まない領域 Ω 内部の位置 r Ω\ Ω における音圧 p(r) は, 境界面 Ω 上の積分方程式によって以下のように得られる ( ) p(r) = G(r r ) p(r ) n p(r ) G(r r ) n dr Ω 音圧の法線方向微分 p(r)/ n( ここからは音圧勾配と呼ぶ ) は, 周波数領域では粒子速度に比例する量 (cf. 第 7 回の資料 ) p(r) n = jωρv n(r) 境界面 Ω 上の音圧と音圧勾配がわかれば,Kirchhoff Helmholtz 積分方程式にしたがって内部の音圧を求められる 小山翔一 (UTokyo) 応用音響学第 9 回 2021/6/11 27 / 62
28 Kirchhoff Helmholtz 積分方程式 外部問題における Kirchhoff Helmholtz 積分方程式 外部問題の場合, 上図のような 3 つの境界面 S o,s i,s ( 半径が無限大の球面 ) からなる面に対して Green の定理を適用する ( ) ( Φ G(r r ) G(r r ) Φ ) dr = 0 n n S o + S i + S 小山翔一 (UTokyo) 応用音響学第 9 回 2021/6/11 28 / 62
29 Kirchhoff Helmholtz 積分方程式 外部問題における Kirchhoff Helmholtz 積分方程式 S i における積分は内部問題の場合と同様 ( lim Φ G(r r ) G(r r ) Φ ) ds i = ϵ 0 S i n n S Φ(r ) r R 3 \Ω 1 2 Φ(r ) r S o 0 r Ω\S o S における積分は, 球の半径を r として, ( lim Φ G(r r ) G(r r ) Φ ) ds r r r さらに, ejk r r G(r r ) = 4π r r ejkr 4πr ( ) G(r r ) = e jk r r r r 4π r r jk ejkr 4πr 小山翔一 (UTokyo) 応用音響学第 9 回 2021/6/11 29 / 62
30 Kirchhoff Helmholtz 積分方程式 外部問題における Kirchhoff Helmholtz 積分方程式 近似式を使って S における積分を計算すると, ( lim Φ G(r r ) G(r r ) Φ r r r S lim r = lim r e jkr r r ( Φ(r) r ) ds ) jkφ(r) したがって,S における積分を 0 とするためには, 次の関係式が成り立たなければならない ( ) p(r) jkp(r) = 0 ここで Φ を音圧 p に置き換えた この条件は Sommerfeld の放射条件と呼ばれ, 無限遠での境界条件を与えている 小山翔一 (UTokyo) 応用音響学第 9 回 2021/6/11 30 / 62
31 Kirchhoff Helmholtz 積分方程式 外部問題における Kirchhoff Helmholtz 積分方程式 以上により,Helmholtz 方程式の境界値積分表現として, 外部問題における Kirchhoff Helmholtz 積分方程式が得られた 外部問題における Kirchhoff Helmholtz 積分方程式 ある領域 Ω 外部の音源を含まない領域内の位置 r R 3 \Ω における音圧 p(r) は, 境界面 Ω 上の積分方程式によって以下のように得られる ( ) p(r) = G(r r ) p(r ) n p(r ) G(r r ) n dr Ω 小山翔一 (UTokyo) 応用音響学第 9 回 2021/6/11 31 / 62
32 Kirchhoff Helmholtz 積分方程式 外部問題における Kirchhoff Helmholtz 積分方程式 以上により,Helmholtz 方程式の境界値積分表現として, 外部問題における Kirchhoff Helmholtz 積分方程式が得られた 外部問題における Kirchhoff Helmholtz 積分方程式 ある領域 Ω 外部の音源を含まない領域内の位置 r R 3 \Ω における音圧 p(r) は, 境界面 Ω 上の積分方程式によって以下のように得られる ( ) p(r) = G(r r ) p(r ) n p(r ) G(r r ) n dr Ω 境界面 Ω 上の音圧と音圧勾配がわかれば,Kirchhoff Helmholtz 積分方程式にしたがって外部の音圧 ( 放射音場 ) を求められる 式の形としては内部問題の場合と同じだが, 法線方向ベクトルの向きが異なることに注意 ( 内部問題の場合も同様だが,) Ω は物理的な境界と一致している必要はなく, 仮想的な境界面として設定してよい 小山翔一 (UTokyo) 応用音響学第 9 回 2021/6/11 32 / 62
33 Kirchhoff Helmholtz 積分方程式 散乱問題における Kirchhoff Helmholtz 積分方程式 外部問題を変形して,S o 内部に存在する物体による散乱を扱うこともできる 位置 r = r p に存在する点音源による音場を入射場とする 小山翔一 (UTokyo) 応用音響学第 9 回 2021/6/11 33 / 62
34 Kirchhoff Helmholtz 積分方程式 散乱問題における Kirchhoff Helmholtz 積分方程式 位置 r = r p に強度 Φ 0 の点音源による特異点を持つ Φ と, 位置 r = r に特異点を持つ Ψ = G(r r ) は, それぞれ以下を満たす 2 Φ(r) + k 2 Φ(r) = Φ 0 δ(r r p ) 2 G(r r ) + k 2 G(r r ) = δ(r r ) これらに対し,S o,s i,s,s p の境界面において Green の定理を適用する ( ) ( Φ G(r r ) G(r r ) Φ ) dr = 0 n n S o + S i + S + S p S i における積分は外部問題の場合と同様,S における積分は Sommerfeld の放射条件を満たすとして 0 となる 小山翔一 (UTokyo) 応用音響学第 9 回 2021/6/11 34 / 62
35 Kirchhoff Helmholtz 積分方程式 散乱問題における Kirchhoff Helmholtz 積分方程式 S p における積分は, 球 S p の半径を ϵ としたとき,ϵ 0 の場合に点音源近傍では自由空間に置かれた点音源による音場として近似できることから, e jk r rp lim Φ(r) = Φ 0G(r r p ) = Φ 0 ϵ 0 4π r r p よって,S p における積分は S i における積分と同様の形で求められる ( lim G(r r ) Φ ) ϵ 0 n ) Φ G(r r ds p n = G(r p r Φ ) lim ϵ 0 S p n ϵ2 sin θdθdϕ = Φ 0 G(r p r ) この式は入射場と呼ばれ, ここでは p inc と表す 小山翔一 (UTokyo) 応用音響学第 9 回 2021/6/11 35 / 62
36 Kirchhoff Helmholtz 積分方程式 散乱問題における Kirchhoff Helmholtz 積分方程式 散乱問題における Kirchhoff Helmholtz 積分方程式 ある散乱体を含む領域 Ω 外部の位置 r R 3 \Ω における音圧 p(r) は, 入射場を p inc として, 境界面 Ω 上の積分方程式によって以下のように得られる ( ) p(r) = p inc (r) + p(r ) G(r r ) n G(r r ) p(r ) n dr Ω ここで法線方向ベクトルの向きを逆にしていることに注意 小山翔一 (UTokyo) 応用音響学第 9 回 2021/6/11 36 / 62
37 Kirchhoff Helmholtz 積分方程式 散乱問題における Kirchhoff Helmholtz 積分方程式 散乱問題における Kirchhoff Helmholtz 積分方程式 ある散乱体を含む領域 Ω 外部の位置 r R 3 \Ω における音圧 p(r) は, 入射場を p inc として, 境界面 Ω 上の積分方程式によって以下のように得られる ( ) p(r) = p inc (r) + p(r ) G(r r ) n G(r r ) p(r ) n dr Ω ここでは入射場 p inc を位置 r p の点音源としたが,S p の取り方を変えれば領域 R 3 \Ω の音源による任意の p inc に対して上式が成り立つ このように散乱音場は, 入射場 p inc と散乱場 p sct の和として表すことができる p(r) = p inc (r) + p sct (r) ただし,p sct (r) = Ω ( ) p(r ) G(r r ) n G(r r ) p(r ) n dr 小山翔一 (UTokyo) 応用音響学第 9 回 2021/6/11 37 / 62
38 Kirchhoff Helmholtz 積分方程式 音源を含む領域における積分表現 領域に音源を含む場合,Ω 内の音源分布を Q(r) とすると, 音場は以下の非斉次 Helmholtz 方程式を満たす ( 2 + k 2 )p(r) = Q(r) 一方,3 次元自由空間 Green 関数 G(r r ) は以下を満たす ( 2 + k 2 )G(r r ) = δ(r r ) 小山翔一 (UTokyo) 応用音響学第 9 回 2021/6/11 38 / 62
39 Kirchhoff Helmholtz 積分方程式 音源を含む領域における積分表現 両辺に Q(r ) をかけて体積 Ω にわたって積分すると, ( 2 + k 2 ) Q(r )G(r r )dr = δ(r r )Q(r )dr Ω = Q(r) したがって, 音源分布 Q(r) による音場は,Q(r) と G(r r ) の畳み込みとして表される p(r) = Q(r )G(r r )dr Ω 自由空間でない場合は, さらに斉次解の項 p h を加えた形となる p(r) = Q(r )G(r r )dr + p h (r) Ω Ω 小山翔一 (UTokyo) 応用音響学第 9 回 2021/6/11 39 / 62
40 Kirchhoff Helmholtz 積分方程式 音源を含む領域における積分表現 非斉次 Helmholtz 方程式に対して Green の定理を適用すれば, ( ) G(r r ) p(r ) Ω n p(r ) G(r r ) n dr ( = G(r r ) 2 p(r ) p(r ) 2 G(r r ) ) dr Ω ( = G(r r )Q(r ) p(r )δ(r r) ) dr Ω = G(r r )Q(r )dr + p(r) ( ただし,r Ω\ Ω) Ω したがって,r Ω\ Ω のとき, p(r) = Q(r )G(r r )dr Ω ( ) + G(r r ) p(r ) n p(r ) G(r r ) n dr Ω 小山翔一 (UTokyo) 応用音響学第 9 回 2021/6/11 40 / 62
41 境界条件を与えた場合の Green 関数 本日の目次 1 境界値積分表現とその応用 Green 関数とその性質 Kirchhoff Helmholtz 積分方程式境界条件を与えた場合の Green 関数 Single layer potential による音場の積分表現 小山翔一 (UTokyo) 応用音響学第 9 回 2021/6/11 41 / 62
42 境界条件を与えた場合の Green 関数 境界条件を与えた場合の Green 関数 Kirchhoff Helmholtz 積分方程式は, 領域の境界面上の音圧と音圧勾配を用い, 自由空間 Green 関数の項とその法線方向微分の項の和による境界値積分により, 内部あるいは外部の音場を決定できる 境界面上の音圧または音圧勾配のみを用いた積分表現も可能であり, その場合は自由空間 Green 関数の代わりに, 具体的な境界条件を満たすような Green 関数を用いればよい Neumann 境界条件を満たすような Green 関数,Neumann 型 Green 関数 G N は, 境界面 Ω において以下を満たす G N n = 0 このような Green 関数を使えば,Kirchhoff Helmholtz 積分方程式の項が 1 つ消去される p(r) = G N (r r ) p(r ) n dr Ω 小山翔一 (UTokyo) 応用音響学第 9 回 2021/6/11 42 / 62
43 境界条件を与えた場合の Green 関数 境界条件を与えた場合の Green 関数 Dirichlet 型 Green 関数 G D (r r ) は, 境界面 Ω において Dirichlet 境界条件を満たす G D = 0 この場合,Kirchhoff Helmholtz 積分方程式のもう一方の項が消去される p(r) = p(r ) G D(r r ) n dr Ω したがって,Neumann 型 Dirichlet 型 Green 関数が得られれば, 境界面上の音圧または音圧勾配のみから ( 禁止周波数を除いて ) 内部あるいは外部の音場を計算できる 境界条件を与えた場合の Green 関数を求める方法は, 大きく分けて二つある 1 斉次 Helmholtz 方程式を満たす関数 g を用いて, 自由空間 Green 関数との和 G + g が境界条件を満たすように定める方法 2 固有関数系による展開または積分変換をを用いる方法 小山翔一 (UTokyo) 応用音響学第 9 回 2021/6/11 43 / 62
44 境界条件を与えた場合の Green 関数 斉次方程式を満たす関数を用いる構成法 まずは一つ目の方法を Neumann 型 Green 関数の場合について考える 斉次 Helmholtz 方程式を満たすような r と r の関数 g N (r r ) を定義する ( 2 + k 2 )g N = 0 この式に Green の定理を適用すれば, Ω 上の境界値積分は 0 になる よって, 自由空間 Green 関数 G と g N との和 G N を考えると, G N = G + g N この Green 関数も Kirchhoff Helmholtz 積分方程式を満たす ( p(r) = G N (r r ) p(r ) n p(r ) G N(r r ) ) n dr Ω 小山翔一 (UTokyo) 応用音響学第 9 回 2021/6/11 44 / 62
45 境界条件を与えた場合の Green 関数 斉次方程式を満たす関数を用いる構成法 あとは G N が Neumann 境界条件を満たすように g N を決めればよい しかしながら, 実際には境界面が変数分離可能な座標系の 1 変数を固定した面で表現できるような, 単純な形状 ( 平面, 球面, 円筒面など ) の場合にのみ Green 関数の具体的な形が得られる 特に平面境界の場合には鏡像法と呼ばれるテクニックが使える ここでは境界面 Ω が無限大の平面である場合の Neumann 型 Green 関数を求める 小山翔一 (UTokyo) 応用音響学第 9 回 2021/6/11 45 / 62
46 境界条件を与えた場合の Green 関数 平面境界の場合の Green 関数 外部問題における Kirchhoff Helmholtz 積分方程式において, 境界面を上図のように変形する S の半径を r とすれば,S o は無限平面となる Sommerfeld の放射条件を仮定すれば, / n = / z として, 平面境界上で Kirchhoff Helmholtz 積分方程式が成り立つ ( p(r) = p(x, y, 0) G(r r ) z p(x, y ), 0) z G(r r ) dx dy S o 小山翔一 (UTokyo) 応用音響学第 9 回 2021/6/11 46 / 62
47 境界条件を与えた場合の Green 関数 平面境界の場合の Green 関数 Neumann 型 Green 関数を構成するためには,z = 0 において, G N z = 0 を満たす g N を求めることが必要 このような g N を求めるには, 特異点 r の平面に対する鏡像位置 r i = (x, y, z) にある仮想的な波源を考えればよい 小山翔一 (UTokyo) 応用音響学第 9 回 2021/6/11 47 / 62
48 境界条件を与えた場合の Green 関数 平面境界の場合の Green 関数 具体的には,g N を以下のように定義する g N (r r ) = G(r i r ) = ejk r i r 4π r i r このとき g N は Ω 内に特異点を持たないので, 斉次 Helmholtz 方程式を満たす したがって, これを自由空間 Green 関数に加えると, G N (r r ) = ejk r r 4π r r + ejk ri r 4π r i r z = 0 において, r r = r i r となるので, G N z = 0 z =0 よって G N は Neumann 境界条件を満たす 小山翔一 (UTokyo) 応用音響学第 9 回 2021/6/11 48 / 62
49 境界条件を与えた場合の Green 関数 平面境界の場合の Green 関数 さらに,z = 0 において,G N は自由空間 Green 関数の 2 倍となる G N z =0 = ejk r r 2π r r よって,Kirchhoff Helmholtz 積分方程式の Green 関数に対してこの G N を用いれば, p(r) = p(x, y, 0) z e jk r r 2π r r dx dy この式は z = 0 の無限平面から z > 0 の音の伝播を記述する重要な式であり, 第 1 種 Raylegih 積分と呼ばれる 小山翔一 (UTokyo) 応用音響学第 9 回 2021/6/11 49 / 62
50 境界条件を与えた場合の Green 関数 平面境界の場合の Green 関数 ちなみに,Dirichlet 型 Green 関数を構成する場合は, 同じように鏡像波源を考えて, とすればよい G D (r r ) = ejk r r 4π r r ejk ri r 4π r i r この場合,z = 0 の平面において Dirichlet 境界条件 G D z = 0 が満たされ, 以下の第 2 種 Rayleigh 積分が得られる p(r) = p(x, y, 0) z e jk r r 2π r r dx dy 鏡像法が使えない球状の境界面の場合などは次回 小山翔一 (UTokyo) 応用音響学第 9 回 2021/6/11 50 / 62
51 境界条件を与えた場合の Green 関数 Rayleigh 積分の近似 光学の分野でよく出てくる回折の式は,Rayleigh 積分を近似し, 積分区間を開口部とすることで導ける フレネル回折 開口部の大きさがスクリーンまでの距離 R に対して十分小さいとすれば,A を振幅として以下の Fresnel 回折の式が得られる p(r) = A jλr ejkr p(x, y, 0)e jk 2R [(x x ) 2 +(y y ) 2] dx dy さらに近似をすることで Fraunhofer 回折の式が得られる 小山翔一 (UTokyo) 応用音響学第 9 回 2021/6/11 51 / 62
52 境界条件を与えた場合の Green 関数 固有関数展開による Green 関数の構成法 もう一つの Green 関数の構成法として, 固有関数による展開に基づく方法を考える ここで固有関数とは, ある境界条件を満たす領域内の共振に対応する 3 次元のモード形状を指す ( ただし内部音圧に対しては境界条件を指定しない ) 音源を含まない領域 Ω 内部の音場は, 以下の斉次 Helmholtz 方程式を満たす 2 p(r) + k 2 p(r) = 0 Dirichlet 型 Green 関数は, 以下の非斉次 Helmholtz 方程式および境界面 Ω における Dirichlet 境界条件を満たせばよい { 2 G D (r r ) + k 2 G D (r r ) = δ(r r ) G D (r r ) = 0, r Ω 小山翔一 (UTokyo) 応用音響学第 9 回 2021/6/11 52 / 62
53 境界条件を与えた場合の Green 関数 固有関数展開による Green 関数の構成法 このような Green 関数を使うと,Kirchhoff Helmholtz 積分方程式が単純化される p(r) = p(r ) G D(r r ) n dr Ω ここで, 領域 Ω の 3 次元固有関数 Ψ q (r) が既知であるとする この固有関数は G D と同じ境界条件を満たし,k q = ω q /c で与えられる固有周波数を持つものとする ここで q は固有関数の番号である これらの固有関数が完全直交系をなすと仮定すると, 領域 Ω 内の任意の音圧分布が固有関数の線形和として表現できる 係数を A q (r ) とすれば, G D (r r ) = q A q (r )Ψ q (r) 小山翔一 (UTokyo) 応用音響学第 9 回 2021/6/11 53 / 62
54 境界条件を与えた場合の Green 関数 固有関数展開による Green 関数の構成法 Ψ q は領域 Ω の固有関数なので, 斉次 Helmholtz 方程式を満たす固有値 k q を持つ 2 Ψ q + k 2 qψ q = 0 G D の固有関数展開の式を非斉次 Helmholtz 方程式に代入し, 上式を用いると, A q ( kq 2 + k 2 )Ψ q (r) = δ(r r ) q 両辺に Ψ q (r) をかけて, 領域 Ω にわたって積分すると, A q (k 2 kq) 2 Ψ q (r)ψ q (r) dr = Ψ q (r ) したがって, Ω Ψ q (r ) A q = (k 2 kq) 2 Ω Ψ q(r)ψ q (r) dr 小山翔一 (UTokyo) 応用音響学第 9 回 2021/6/11 54 / 62
55 境界条件を与えた場合の Green 関数 固有関数展開による Green 関数の構成法 以上の結果から,Dirichlet 型 Green 関数が以下のように得られる G D (r r ) = q Ψ q (r)ψ q (r ) (k 2 q k 2 ) Ω Ψ q(r)ψ q (r) dr Neumann 型 Green 関数についても同様の手続きで導出できる ( 最終的に同じ形になる ) ただし,k = k q の場合, 境界面 Ω での音圧が 0 となり, 内部音圧を計算することができない これは Dirichlet 型 Green 関数の分母が 0 になることにも表れている これは固有関数を用いる場合以外の方法でも共通の問題であるが, 閉じた境界面に対する Neumann 型 Dirichlet 型 Green 関数は禁止周波数において計算できない また, 固有関数をどのように得るかという問題が残っているが, これを具体的な関数として得られるのは Ω が単純な形状の場合に限られる 小山翔一 (UTokyo) 応用音響学第 9 回 2021/6/11 55 / 62
56 Single layer potential による音場の積分表現 本日の目次 1 境界値積分表現とその応用 Green 関数とその性質 Kirchhoff Helmholtz 積分方程式境界条件を与えた場合の Green 関数 Single layer potential による音場の積分表現 小山翔一 (UTokyo) 応用音響学第 9 回 2021/6/11 56 / 62
57 Single layer potential による音場の積分表現 Single layer potential による音場の積分表現 Kirchhoff Helmholtz 積分方程式は, 領域の境界面上の音圧と音圧勾配を用い, 自由空間 Green 関数の項とその法線方向微分の項の和による境界値積分により, 内部あるいは外部の音場を決定できるというものであった 自由空間 Green 関数の項のみを用いる積分表現として,single layer potential( あるいは単純波源の定式化 :simple source formulation, 等価音源法 :equivalent source method とも呼ぶ ) がある 小山翔一 (UTokyo) 応用音響学第 9 回 2021/6/11 57 / 62
58 Single layer potential による音場の積分表現 Single layer potential による音場の積分表現 境界面 Ω とその内部領域 外部領域をそれぞれ Ω int,ω ext として定義し, 以下の積分表現を考える p(r) = µ(r )G(r r )dr Ω つまり自由空間 Green 関数の項のみを用いる ここで法線方向が逆になっていることに注意 小山翔一 (UTokyo) 応用音響学第 9 回 2021/6/11 58 / 62
59 Single layer potential による音場の積分表現 Single layer potential による音場の積分表現 µ(r) を具体的に導出するため, 外部 内部問題における Kirchhoff Helmholtz 積分方程式を思い出すと, p ext (r) (r Ω ext ) p ext (r)/2 (r Ω) 0 (r Ω int ) ( = G(r r ) p ext(r ) Ω n p ext (r) G(r r ) n 0 (r Ω ext ) p int (r)/2 (r Ω) p int (r) (r Ω int ) = Ω ( G(r r ) p int(r ) n p int (r) G(r r ) n ) dr ) dr 法線方向が領域の内側を向いているため, 内部問題に関しては正負が逆になっている 小山翔一 (UTokyo) 応用音響学第 9 回 2021/6/11 59 / 62
60 Single layer potential による音場の積分表現 Single layer potential による音場の積分表現 r Ω において,p ext (r) = p int (r), p ext (r)/ n p int (r)/ n として, 外部問題の式から内部問題の式を引くと, p ext (r) (r Ω ext ) p int (r) = p ext (r) (r Ω) p int (r) (r Ω int ) ( pext (r ) = n p int(r ) ) n G(r r )dr Ω したがって,µ(r) は外部 内部領域の Ω 上の音圧勾配の差となる µ(r) = p ext(r) n p int(r) n この関係式は jump relation と呼ばれる Single layer potential は内部問題 外部問題どちらかに対して適用できるものであり, 両方同時に適用できるわけではない 小山翔一 (UTokyo) 応用音響学第 9 回 2021/6/11 60 / 62
61 Single layer potential による音場の積分表現 Single layer potential による音場の積分表現 Single layer potential を用いて境界面 Ω 上の音圧勾配を導出する場合は, 外部 内部音場で音圧勾配が不連続であることに注意が必要 不連続面における音圧勾配を両側の値の平均として定義すれば, µ(r ) G(r r ) n dr = 1 ( pext (r) + p ) int(r) (r Ω) 2 n n Ω このとき,µ(r) の定義より, ( 1 pext (r) + p ) int(r) 2 n n = µ(r) 2 + p ext(r) n よって, 例えば外部問題の場合, p ext (r) = µ(r) + µ(r ) G(r r ) n 2 n dr (r Ω) Ω 小山翔一 (UTokyo) 応用音響学第 9 回 2021/6/11 61 / 62
62 Single layer potential による音場の積分表現 参考文献 今村勤 (2017) 物理とグリーン関数岩波書店, Tokyo. E. G. Williams (1999) Fourier Acoustics: Sound Radiation and Nearfield Acoustical Holography Academic Presss, Cambridge. D. Colton and R. Kress (2013) Inverse Acoustic and Electromagnetic Scattering Theory Springer, New York. 小山翔一 (UTokyo) 応用音響学第 9 回 2021/6/11 62 / 62
例 e 指数関数的に減衰する信号を h( a < + a a すると, それらのラプラス変換は, H ( ) { e } e インパルス応答が h( a < ( ただし a >, U( ) { } となるシステムにステップ信号 ( y( のラプラス変換 Y () は, Y ( ) H ( ) X (
 第 週ラプラス変換 教科書 p.34~ 目標ラプラス変換の定義と意味を理解する フーリエ変換や Z 変換と並ぶ 信号解析やシステム設計における重要なツール ラプラス変換は波動現象や電気回路など様々な分野で 微分方程式を解くために利用されてきた ラプラス変換を用いることで微分方程式は代数方程式に変換される また 工学上使われる主要な関数のラプラス変換は簡単な形の関数で表されるので これを ラプラス変換表
第 週ラプラス変換 教科書 p.34~ 目標ラプラス変換の定義と意味を理解する フーリエ変換や Z 変換と並ぶ 信号解析やシステム設計における重要なツール ラプラス変換は波動現象や電気回路など様々な分野で 微分方程式を解くために利用されてきた ラプラス変換を用いることで微分方程式は代数方程式に変換される また 工学上使われる主要な関数のラプラス変換は簡単な形の関数で表されるので これを ラプラス変換表
微分方程式による現象記述と解きかた
 微分方程式による現象記述と解きかた 土木工学 : 公共諸施設 構造物の有用目的にむけた合理的な実現をはかる方法 ( 技術 ) に関する学 橋梁 トンネル ダム 道路 港湾 治水利水施設 安全化 利便化 快適化 合法則的 経済的 自然および人口素材によって作られた 質量保存則 構造物の自然的な性質 作用 ( 外力による応答 ) エネルギー則 の解明 社会的諸現象のうち マスとしての移動 流通 運動量則
微分方程式による現象記述と解きかた 土木工学 : 公共諸施設 構造物の有用目的にむけた合理的な実現をはかる方法 ( 技術 ) に関する学 橋梁 トンネル ダム 道路 港湾 治水利水施設 安全化 利便化 快適化 合法則的 経済的 自然および人口素材によって作られた 質量保存則 構造物の自然的な性質 作用 ( 外力による応答 ) エネルギー則 の解明 社会的諸現象のうち マスとしての移動 流通 運動量則
スライド 1
 暫定版修正 加筆の可能性あり ( 付録 球面波 回折 (. グリーンの定理. キルヒホッフの積分定理 3. ホイヘンスの原理 4. キルヒホッフの回折公式 5. ゾンマーフェルトの放射条件 6. 補足 付録 (90~904 のアプローチ : 回折 (diffaction までの道標. 球面波 (pheical wave のみ対象 : スカラー表示. 虚数単位 i を使用する 3. お詫び : 自己流かつ説明が飛躍する場面があります
暫定版修正 加筆の可能性あり ( 付録 球面波 回折 (. グリーンの定理. キルヒホッフの積分定理 3. ホイヘンスの原理 4. キルヒホッフの回折公式 5. ゾンマーフェルトの放射条件 6. 補足 付録 (90~904 のアプローチ : 回折 (diffaction までの道標. 球面波 (pheical wave のみ対象 : スカラー表示. 虚数単位 i を使用する 3. お詫び : 自己流かつ説明が飛躍する場面があります
パソコンシミュレータの現状
 第 2 章微分 偏微分, 写像 豊橋技術科学大学森謙一郎 2. 連続関数と微分 工学において物理現象を支配する方程式は微分方程式で表されていることが多く, 有限要素法も微分方程式を解く数値解析法であり, 定式化においては微分 積分が一般的に用いられており. 数学の基礎知識が必要になる. 図 2. に示すように, 微分は連続な関数 f() の傾きを求めることであり, 微小な に対して傾きを表し, を無限に
第 2 章微分 偏微分, 写像 豊橋技術科学大学森謙一郎 2. 連続関数と微分 工学において物理現象を支配する方程式は微分方程式で表されていることが多く, 有限要素法も微分方程式を解く数値解析法であり, 定式化においては微分 積分が一般的に用いられており. 数学の基礎知識が必要になる. 図 2. に示すように, 微分は連続な関数 f() の傾きを求めることであり, 微小な に対して傾きを表し, を無限に
DVIOUT-SS_Ma
 第 章 微分方程式 ニュートンはリンゴが落ちるのを見て万有引力を発見した という有名な逸話があります 無重力の宇宙船の中ではリンゴは落ちないで静止していることを考えると 重力が働くと始め静止しているものが動き出して そのスピードはどんどん大きくなる つまり速度の変化が現れることがわかります 速度は一般に時間と共に変化します 速度の瞬間的変化の割合を加速度といい で定義しましょう 速度が変化する, つまり加速度がでなくなるためにはその原因があり
第 章 微分方程式 ニュートンはリンゴが落ちるのを見て万有引力を発見した という有名な逸話があります 無重力の宇宙船の中ではリンゴは落ちないで静止していることを考えると 重力が働くと始め静止しているものが動き出して そのスピードはどんどん大きくなる つまり速度の変化が現れることがわかります 速度は一般に時間と共に変化します 速度の瞬間的変化の割合を加速度といい で定義しましょう 速度が変化する, つまり加速度がでなくなるためにはその原因があり
2009 年 11 月 16 日版 ( 久家 ) 遠地 P 波の変位波形の作成 遠地 P 波の変位波形 ( 変位の時間関数 ) は 波線理論をもとに P U () t = S()* t E()* t P() t で近似的に計算できる * は畳み込み積分 (convolution) を表す ( 付録
 遠地 波の変位波形の作成 遠地 波の変位波形 ( 変位の時間関数 ) は 波線理論をもとに U () t S() t E() t () t で近似的に計算できる は畳み込み積分 (convolution) を表す ( 付録 参照 ) ここで St () は地震の断層運動によって決まる時間関数 1 E() t は地下構造によって生じる種々の波の到着を与える時間関数 ( ここでは 直達 波とともに 震源そばの地表での反射波や変換波を与える時間関数
遠地 波の変位波形の作成 遠地 波の変位波形 ( 変位の時間関数 ) は 波線理論をもとに U () t S() t E() t () t で近似的に計算できる は畳み込み積分 (convolution) を表す ( 付録 参照 ) ここで St () は地震の断層運動によって決まる時間関数 1 E() t は地下構造によって生じる種々の波の到着を与える時間関数 ( ここでは 直達 波とともに 震源そばの地表での反射波や変換波を与える時間関数
Microsoft PowerPoint - H21生物計算化学2.ppt
 演算子の行列表現 > L いま 次元ベクトル空間の基底をケットと書くことにする この基底は完全系を成すとすると 空間内の任意のケットベクトルは > > > これより 一度基底を与えてしまえば 任意のベクトルはその基底についての成分で完全に記述することができる これらの成分を列行列の形に書くと M これをベクトル の基底 { >} による行列表現という ところで 行列 A の共役 dont 行列は A
演算子の行列表現 > L いま 次元ベクトル空間の基底をケットと書くことにする この基底は完全系を成すとすると 空間内の任意のケットベクトルは > > > これより 一度基底を与えてしまえば 任意のベクトルはその基底についての成分で完全に記述することができる これらの成分を列行列の形に書くと M これをベクトル の基底 { >} による行列表現という ところで 行列 A の共役 dont 行列は A
0 21 カラー反射率 slope aspect 図 2.9: 復元結果例 2.4 画像生成技術としての計算フォトグラフィ 3 次元情報を復元することにより, 画像生成 ( レンダリング ) に応用することが可能である. 近年, コンピュータにより, カメラで直接得られない画像を生成する技術分野が生
 0 21 カラー反射率 slope aspect 図 2.9: 復元結果例 2.4 画像生成技術としての計算フォトグラフィ 3 次元情報を復元することにより, 画像生成 ( レンダリング ) に応用することが可能である. 近年, コンピュータにより, カメラで直接得られない画像を生成する技術分野が生まれ, コンピューテーショナルフォトグラフィ ( 計算フォトグラフィ ) と呼ばれている.3 次元画像認識技術の計算フォトグラフィへの応用として,
0 21 カラー反射率 slope aspect 図 2.9: 復元結果例 2.4 画像生成技術としての計算フォトグラフィ 3 次元情報を復元することにより, 画像生成 ( レンダリング ) に応用することが可能である. 近年, コンピュータにより, カメラで直接得られない画像を生成する技術分野が生まれ, コンピューテーショナルフォトグラフィ ( 計算フォトグラフィ ) と呼ばれている.3 次元画像認識技術の計算フォトグラフィへの応用として,
Microsoft Word - 1B2011.doc
 第 14 回モールの定理 ( 単純梁の場合 ) ( モールの定理とは何か?p.11) 例題 下記に示す単純梁の C 点のたわみ角 θ C と, たわみ δ C を求めよ ただし, 部材の曲げ 剛性は材軸に沿って一様で とする C D kn B 1.5m 0.5m 1.0m 解答 1 曲げモーメント図を描く,B 点の反力を求める kn kn 4 kn 曲げモーメント図を描く knm 先に得られた曲げモーメントの値を
第 14 回モールの定理 ( 単純梁の場合 ) ( モールの定理とは何か?p.11) 例題 下記に示す単純梁の C 点のたわみ角 θ C と, たわみ δ C を求めよ ただし, 部材の曲げ 剛性は材軸に沿って一様で とする C D kn B 1.5m 0.5m 1.0m 解答 1 曲げモーメント図を描く,B 点の反力を求める kn kn 4 kn 曲げモーメント図を描く knm 先に得られた曲げモーメントの値を
vecrot
 1. ベクトル ベクトル : 方向を持つ量 ベクトルには 1 方向 2 大きさ ( 長さ ) という 2 つの属性がある ベクトルの例 : 物体の移動速度 移動量電場 磁場の強さ風速力トルクなど 2. ベクトルの表現 2.1 矢印で表現される 矢印の長さ : ベクトルの大きさ 矢印の向き : ベクトルの方向 2.2 2 個の点を用いて表現する 始点 () と終点 () を結ぶ半直線の向き : ベクトルの方向
1. ベクトル ベクトル : 方向を持つ量 ベクトルには 1 方向 2 大きさ ( 長さ ) という 2 つの属性がある ベクトルの例 : 物体の移動速度 移動量電場 磁場の強さ風速力トルクなど 2. ベクトルの表現 2.1 矢印で表現される 矢印の長さ : ベクトルの大きさ 矢印の向き : ベクトルの方向 2.2 2 個の点を用いて表現する 始点 () と終点 () を結ぶ半直線の向き : ベクトルの方向
PowerPoint Presentation
 付録 2 2 次元アフィン変換 直交変換 たたみ込み 1.2 次元のアフィン変換 座標 (x,y ) を (x,y) に移すことを 2 次元での変換. 特に, 変換が と書けるとき, アフィン変換, アフィン変換は, その 1 次の項による変換 と 0 次の項による変換 アフィン変換 0 次の項は平行移動 1 次の項は座標 (x, y ) をベクトルと考えて とすれば このようなもの 2 次元ベクトルの線形写像
付録 2 2 次元アフィン変換 直交変換 たたみ込み 1.2 次元のアフィン変換 座標 (x,y ) を (x,y) に移すことを 2 次元での変換. 特に, 変換が と書けるとき, アフィン変換, アフィン変換は, その 1 次の項による変換 と 0 次の項による変換 アフィン変換 0 次の項は平行移動 1 次の項は座標 (x, y ) をベクトルと考えて とすれば このようなもの 2 次元ベクトルの線形写像
Chap2.key
 . f( ) V (V V ) V e + V e V V V V ( ) V V ( ) E. - () V (0 ) () V (0 ) () V (0 ) (4) V ( ) E. - () V (0 ) () V (0 ) O r θ ( ) ( ) : (r θ) : { r cos θ r sn θ { r + () V (0 ) (4) V ( ) θ θ arg( ) : π π
. f( ) V (V V ) V e + V e V V V V ( ) V V ( ) E. - () V (0 ) () V (0 ) () V (0 ) (4) V ( ) E. - () V (0 ) () V (0 ) O r θ ( ) ( ) : (r θ) : { r cos θ r sn θ { r + () V (0 ) (4) V ( ) θ θ arg( ) : π π
第 4 週コンボリューションその 2, 正弦波による分解 教科書 p. 16~ 目標コンボリューションの演習. 正弦波による信号の分解の考え方の理解. 正弦波の複素表現を学ぶ. 演習問題 問 1. 以下の図にならって,1 と 2 の δ 関数を図示せよ δ (t) 2
 第 4 週コンボリューションその, 正弦波による分解 教科書 p. 6~ 目標コンボリューションの演習. 正弦波による信号の分解の考え方の理解. 正弦波の複素表現を学ぶ. 演習問題 問. 以下の図にならって, と の δ 関数を図示せよ. - - - δ () δ ( ) - - - 図 δ 関数の図示の例 δ ( ) δ ( ) δ ( ) δ ( ) δ ( ) - - - - - - - -
第 4 週コンボリューションその, 正弦波による分解 教科書 p. 6~ 目標コンボリューションの演習. 正弦波による信号の分解の考え方の理解. 正弦波の複素表現を学ぶ. 演習問題 問. 以下の図にならって, と の δ 関数を図示せよ. - - - δ () δ ( ) - - - 図 δ 関数の図示の例 δ ( ) δ ( ) δ ( ) δ ( ) δ ( ) - - - - - - - -
数学 t t t t t 加法定理 t t t 倍角公式加法定理で α=β と置く. 三角関数
 . 三角関数 基本関係 t cot c sc c cot sc t 還元公式 t t t t t t cot t cot t 数学 数学 t t t t t 加法定理 t t t 倍角公式加法定理で α=β と置く. 三角関数 数学. 三角関数 5 積和公式 6 和積公式 数学. 三角関数 7 合成 t V v t V v t V V V V VV V V V t V v v 8 べき乗 5 6 6
. 三角関数 基本関係 t cot c sc c cot sc t 還元公式 t t t t t t cot t cot t 数学 数学 t t t t t 加法定理 t t t 倍角公式加法定理で α=β と置く. 三角関数 数学. 三角関数 5 積和公式 6 和積公式 数学. 三角関数 7 合成 t V v t V v t V V V V VV V V V t V v v 8 べき乗 5 6 6
SAP11_03
 第 3 回 音声音響信号処理 ( 線形予測分析と自己回帰モデル ) 亀岡弘和 東京大学大学院情報理工学系研究科日本電信電話株式会社 NTT コミュニケーション科学基礎研究所 講義内容 ( キーワード ) 信号処理 符号化 標準化の実用システム例の紹介情報通信の基本 ( 誤り検出 訂正符号 変調 IP) 符号化技術の基本 ( 量子化 予測 変換 圧縮 ) 音声分析 合成 認識 強調 音楽信号処理統計的信号処理の基礎
第 3 回 音声音響信号処理 ( 線形予測分析と自己回帰モデル ) 亀岡弘和 東京大学大学院情報理工学系研究科日本電信電話株式会社 NTT コミュニケーション科学基礎研究所 講義内容 ( キーワード ) 信号処理 符号化 標準化の実用システム例の紹介情報通信の基本 ( 誤り検出 訂正符号 変調 IP) 符号化技術の基本 ( 量子化 予測 変換 圧縮 ) 音声分析 合成 認識 強調 音楽信号処理統計的信号処理の基礎
<4D F736F F D20824F B CC92E8979D814696CA90CF95AA82C691CC90CF95AA2E646F63>
 1/1 平成 23 年 3 月 24 日午後 6 時 52 分 6 ガウスの定理 : 面積分と体積分 6 ガウスの定理 : 面積分と体積分 Ⅰ. 直交座標系 ガウスの定理は 微分して すぐに積分すると元に戻るというルールを 3 次元積分に適用した定理になります よく知っているのは 簡単化のため 変数が1つの場合は dj ( d ( ににします全微分 = 偏微分 d = d = J ( + C d です
1/1 平成 23 年 3 月 24 日午後 6 時 52 分 6 ガウスの定理 : 面積分と体積分 6 ガウスの定理 : 面積分と体積分 Ⅰ. 直交座標系 ガウスの定理は 微分して すぐに積分すると元に戻るというルールを 3 次元積分に適用した定理になります よく知っているのは 簡単化のため 変数が1つの場合は dj ( d ( ににします全微分 = 偏微分 d = d = J ( + C d です
PowerPoint プレゼンテーション
 米田 戸倉川月 7 限 193~21 西 5-19 応用数学 A 積分定理 Gaussの定理 divbd = B nds Stokesの定理 E bds = E dr Green の定理 g x f y dxdy = fdx + gdy = f e i + ge j dr Gauss の発散定理 S n FdS = Fd 1777-1855 ドイツ Johann arl Friedrich Gauss
米田 戸倉川月 7 限 193~21 西 5-19 応用数学 A 積分定理 Gaussの定理 divbd = B nds Stokesの定理 E bds = E dr Green の定理 g x f y dxdy = fdx + gdy = f e i + ge j dr Gauss の発散定理 S n FdS = Fd 1777-1855 ドイツ Johann arl Friedrich Gauss
PowerPoint プレゼンテーション
 電磁波工学 第 5 回平面波の媒質への垂直および射入射と透過 柴田幸司 Bounda Plan Rgon ε μ Rgon Mdum ( ガラスなど ε μ z 平面波の反射と透過 垂直入射の場合 左図に示す様に 平面波が境界面に対して垂直に入射する場合を考える この時の入射波を とすると 入射波は境界において 透過波 と とに分解される この時の透過量を 反射量を Γ とおくと 領域 における媒質の誘電率に対して透過量
電磁波工学 第 5 回平面波の媒質への垂直および射入射と透過 柴田幸司 Bounda Plan Rgon ε μ Rgon Mdum ( ガラスなど ε μ z 平面波の反射と透過 垂直入射の場合 左図に示す様に 平面波が境界面に対して垂直に入射する場合を考える この時の入射波を とすると 入射波は境界において 透過波 と とに分解される この時の透過量を 反射量を Γ とおくと 領域 における媒質の誘電率に対して透過量
数値計算で学ぶ物理学 4 放物運動と惑星運動 地上のように下向きに重力がはたらいているような場においては 物体を投げると放物運動をする 一方 中心星のまわりの重力場中では 惑星は 円 だ円 放物線または双曲線を描きながら運動する ここでは 放物運動と惑星運動を 運動方程式を導出したうえで 数値シミュ
 数値計算で学ぶ物理学 4 放物運動と惑星運動 地上のように下向きに重力がはたらいているような場においては 物体を投げると放物運動をする 一方 中心星のまわりの重力場中では 惑星は 円 だ円 放物線または双曲線を描きながら運動する ここでは 放物運動と惑星運動を 運動方程式を導出したうえで 数値シミュレーションによって計算してみる 4.1 放物運動一様な重力場における放物運動を考える 一般に質量の物体に作用する力をとすると運動方程式は
数値計算で学ぶ物理学 4 放物運動と惑星運動 地上のように下向きに重力がはたらいているような場においては 物体を投げると放物運動をする 一方 中心星のまわりの重力場中では 惑星は 円 だ円 放物線または双曲線を描きながら運動する ここでは 放物運動と惑星運動を 運動方程式を導出したうえで 数値シミュレーションによって計算してみる 4.1 放物運動一様な重力場における放物運動を考える 一般に質量の物体に作用する力をとすると運動方程式は
OCW-iダランベールの原理
 講義名連続体力学配布資料 OCW- 第 2 回ダランベールの原理 無機材料工学科准教授安田公一 1 はじめに今回の講義では, まず, 前半でダランベールの原理について説明する これを用いると, 動力学の問題を静力学の問題として解くことができ, さらに, 前回の仮想仕事の原理を適用すると動力学問題も簡単に解くことができるようになる また, 後半では, ダランベールの原理の応用として ラグランジュ方程式の導出を示す
講義名連続体力学配布資料 OCW- 第 2 回ダランベールの原理 無機材料工学科准教授安田公一 1 はじめに今回の講義では, まず, 前半でダランベールの原理について説明する これを用いると, 動力学の問題を静力学の問題として解くことができ, さらに, 前回の仮想仕事の原理を適用すると動力学問題も簡単に解くことができるようになる また, 後半では, ダランベールの原理の応用として ラグランジュ方程式の導出を示す
FEM原理講座 (サンプルテキスト)
 サンプルテキスト FEM 原理講座 サイバネットシステム株式会社 8 年 月 9 日作成 サンプルテキストについて 各講師が 講義の内容が伝わりやすいページ を選びました テキストのページは必ずしも連続していません 一部を抜粋しています 幾何光学講座については 実物のテキストではなくガイダンスを掲載いたします 対象とする構造系 物理モデル 連続体 固体 弾性体 / 弾塑性体 / 粘弾性体 / 固体
サンプルテキスト FEM 原理講座 サイバネットシステム株式会社 8 年 月 9 日作成 サンプルテキストについて 各講師が 講義の内容が伝わりやすいページ を選びました テキストのページは必ずしも連続していません 一部を抜粋しています 幾何光学講座については 実物のテキストではなくガイダンスを掲載いたします 対象とする構造系 物理モデル 連続体 固体 弾性体 / 弾塑性体 / 粘弾性体 / 固体
応用数学A
 応用数学 A 米田 戸倉川月 7 限 1930~2100 西 5-109 V を :x 2 + y 2 + z 2 = 4 で囲まれる内部とする F = ye x xe y + ze z FdV = V e x e y e z F = = 2e z 2e z dv = 2e z 3 23 = 64π 3 e z y x z 4π V n Fd = 1 F nd 2 F nd 法線ベクトル n g x,
応用数学 A 米田 戸倉川月 7 限 1930~2100 西 5-109 V を :x 2 + y 2 + z 2 = 4 で囲まれる内部とする F = ye x xe y + ze z FdV = V e x e y e z F = = 2e z 2e z dv = 2e z 3 23 = 64π 3 e z y x z 4π V n Fd = 1 F nd 2 F nd 法線ベクトル n g x,
Microsoft PowerPoint - 物情数学C(2012)(フーリエ前半)_up
 年度物理情報工学科 年生秋学期 物理情報数学 C フーリエ解析 (Fourier lysis) 年 月 5 日 フーリエ ( フランス ) (768~83: ナポレオンの時代 ) 歳で Ecole Polyechique ( フランス国立理工科大学 ) の教授 ナポレオンのエジプト遠征に従軍 (798) 87: 任意の関数は三角関数によって級数展開できる という フーリエ級数 の概念を提唱 ( 論文を提出
年度物理情報工学科 年生秋学期 物理情報数学 C フーリエ解析 (Fourier lysis) 年 月 5 日 フーリエ ( フランス ) (768~83: ナポレオンの時代 ) 歳で Ecole Polyechique ( フランス国立理工科大学 ) の教授 ナポレオンのエジプト遠征に従軍 (798) 87: 任意の関数は三角関数によって級数展開できる という フーリエ級数 の概念を提唱 ( 論文を提出
ニュートン重力理論.pptx
 3 ニュートン重力理論 1. ニュートン重力理論の基本 : 慣性系とガリレイ変換不変性 2. ニュートン重力理論の定式化 3. 等価原理 4. 流体力学方程式とその基礎 3.1 ニュートン重力理論の基本 u ニュートンの第一法則 = 力がかからなければ 等速直線運動を続ける u 等速直線運動に見える系を 慣性系 と呼ぶ ² 直線とはどんな空間の直線か? ニュートン理論では 3 次元ユークリッド空間
3 ニュートン重力理論 1. ニュートン重力理論の基本 : 慣性系とガリレイ変換不変性 2. ニュートン重力理論の定式化 3. 等価原理 4. 流体力学方程式とその基礎 3.1 ニュートン重力理論の基本 u ニュートンの第一法則 = 力がかからなければ 等速直線運動を続ける u 等速直線運動に見える系を 慣性系 と呼ぶ ² 直線とはどんな空間の直線か? ニュートン理論では 3 次元ユークリッド空間
解析力学B - 第11回: 正準変換
 解析力学 B 第 11 回 : 正準変換 神戸大 : 陰山聡 ホームページ ( 第 6 回から今回までの講義ノート ) http://tinyurl.com/kage2010 2011.01.27 正準変換 バネ問題 ( あえて下手に座標をとった ) ハミルトニアンを考える q 正準方程式は H = p2 2m + k 2 (q l 0) 2 q = H p = p m ṗ = H q = k(q
解析力学 B 第 11 回 : 正準変換 神戸大 : 陰山聡 ホームページ ( 第 6 回から今回までの講義ノート ) http://tinyurl.com/kage2010 2011.01.27 正準変換 バネ問題 ( あえて下手に座標をとった ) ハミルトニアンを考える q 正準方程式は H = p2 2m + k 2 (q l 0) 2 q = H p = p m ṗ = H q = k(q
第1章 単 位
 H. Hamano,. 長柱の座屈 - 長柱の座屈 長い柱は圧縮荷重によって折れてしまう場合がある. この現象を座屈といい, 座屈するときの荷重を座屈荷重という.. 換算長 長さ の柱に荷重が作用する場合, その支持方法によって, 柱の理論上の長さ L が異なる. 長柱の計算は, この L を用いて行うと都合がよい. この L を換算長 ( あるいは有効長さという ) という. 座屈荷重は一般に,
H. Hamano,. 長柱の座屈 - 長柱の座屈 長い柱は圧縮荷重によって折れてしまう場合がある. この現象を座屈といい, 座屈するときの荷重を座屈荷重という.. 換算長 長さ の柱に荷重が作用する場合, その支持方法によって, 柱の理論上の長さ L が異なる. 長柱の計算は, この L を用いて行うと都合がよい. この L を換算長 ( あるいは有効長さという ) という. 座屈荷重は一般に,
以下 変数の上のドットは時間に関する微分を表わしている (ex. 2 dx d x x, x 2 dt dt ) 付録 E 非線形微分方程式の平衡点の安定性解析 E-1) 非線形方程式の線形近似特に言及してこなかったが これまでは線形微分方程式 ( x や x, x などがすべて 1 次で なおかつ
 以下 変数の上のドットは時間に関する微分を表わしている (e. d d, dt dt ) 付録 E 非線形微分方程式の平衡点の安定性解析 E-) 非線形方程式の線形近似特に言及してこなかったが これまでは線形微分方程式 ( や, などがすべて 次で なおかつそれらの係数が定数であるような微分方程式 ) に対して安定性の解析を行ってきた しかしながら 実際には非線形の微分方程式で記述される現象も多く存在する
以下 変数の上のドットは時間に関する微分を表わしている (e. d d, dt dt ) 付録 E 非線形微分方程式の平衡点の安定性解析 E-) 非線形方程式の線形近似特に言及してこなかったが これまでは線形微分方程式 ( や, などがすべて 次で なおかつそれらの係数が定数であるような微分方程式 ) に対して安定性の解析を行ってきた しかしながら 実際には非線形の微分方程式で記述される現象も多く存在する
Microsoft PowerPoint - シミュレーション工学-2010-第1回.ppt
 シミュレーション工学 ( 後半 ) 東京大学人工物工学研究センター 鈴木克幸 CA( Compter Aded geerg ) r. Jaso Lemo (SC, 98) 設計者が解析ツールを使いこなすことにより 設計の評価 設計の質の向上を図る geerg の本質の 計算機による支援 (CA CAM などより広い名前 ) 様々な汎用ソフトの登場 工業製品の設計に不可欠のツール 構造解析 流体解析
シミュレーション工学 ( 後半 ) 東京大学人工物工学研究センター 鈴木克幸 CA( Compter Aded geerg ) r. Jaso Lemo (SC, 98) 設計者が解析ツールを使いこなすことにより 設計の評価 設計の質の向上を図る geerg の本質の 計算機による支援 (CA CAM などより広い名前 ) 様々な汎用ソフトの登場 工業製品の設計に不可欠のツール 構造解析 流体解析
線積分.indd
 線積分 線積分 ( n, n, n ) (ξ n, η n, ζ n ) ( n-, n-, n- ) (ξ k, η k, ζ k ) ( k, k, k ) ( k-, k-, k- ) 物体に力 を作用させて位置ベクトル A の点 A から位置ベクトル の点 まで曲線 に沿って物体を移動させたときの仕事 W は 次式で計算された A, A, W : d 6 d+ d+ d@,,, d+ d+
線積分 線積分 ( n, n, n ) (ξ n, η n, ζ n ) ( n-, n-, n- ) (ξ k, η k, ζ k ) ( k, k, k ) ( k-, k-, k- ) 物体に力 を作用させて位置ベクトル A の点 A から位置ベクトル の点 まで曲線 に沿って物体を移動させたときの仕事 W は 次式で計算された A, A, W : d 6 d+ d+ d@,,, d+ d+
Probit , Mixed logit
 Probit, Mixed logit 2016/5/16 スタートアップゼミ #5 B4 後藤祥孝 1 0. 目次 Probit モデルについて 1. モデル概要 2. 定式化と理解 3. 推定 Mixed logit モデルについて 4. モデル概要 5. 定式化と理解 6. 推定 2 1.Probit 概要 プロビットモデルとは. 効用関数の誤差項に多変量正規分布を仮定したもの. 誤差項には様々な要因が存在するため,
Probit, Mixed logit 2016/5/16 スタートアップゼミ #5 B4 後藤祥孝 1 0. 目次 Probit モデルについて 1. モデル概要 2. 定式化と理解 3. 推定 Mixed logit モデルについて 4. モデル概要 5. 定式化と理解 6. 推定 2 1.Probit 概要 プロビットモデルとは. 効用関数の誤差項に多変量正規分布を仮定したもの. 誤差項には様々な要因が存在するため,
多次元レーザー分光で探る凝縮分子系の超高速動力学
 波動方程式と量子力学 谷村吉隆 京都大学理学研究科化学専攻 http:theochem.kuchem.kyoto-u.ac.jp TA: 岩元佑樹 iwamoto.y@kuchem.kyoto-u.ac.jp ベクトルと行列の作法 A 列ベクトル c = c c 行ベクトル A = [ c c c ] 転置ベクトル T A = [ c c c ] AA 内積 c AA = [ c c c ] c =
波動方程式と量子力学 谷村吉隆 京都大学理学研究科化学専攻 http:theochem.kuchem.kyoto-u.ac.jp TA: 岩元佑樹 iwamoto.y@kuchem.kyoto-u.ac.jp ベクトルと行列の作法 A 列ベクトル c = c c 行ベクトル A = [ c c c ] 転置ベクトル T A = [ c c c ] AA 内積 c AA = [ c c c ] c =
PowerPoint Presentation
 応用数学 Ⅱ (7) 7 連立微分方程式の立て方と解法. 高階微分方程式による解法. ベクトル微分方程式による解法 3. 演算子による解法 連立微分方程式 未知数が複数個あり, 未知数の数だけ微分方程式が与えられている場合, これらを連立微分方程式という. d d 解法 () 高階微分方程式化による解法 つの方程式から つの未知数を消去して, 未知数が つの方程式に変換 のみの方程式にするために,
応用数学 Ⅱ (7) 7 連立微分方程式の立て方と解法. 高階微分方程式による解法. ベクトル微分方程式による解法 3. 演算子による解法 連立微分方程式 未知数が複数個あり, 未知数の数だけ微分方程式が与えられている場合, これらを連立微分方程式という. d d 解法 () 高階微分方程式化による解法 つの方程式から つの未知数を消去して, 未知数が つの方程式に変換 のみの方程式にするために,
構造力学Ⅰ第12回
 第 回材の座屈 (0 章 ) p.5~ ( 復習 ) モールの定理 ( 手順 ) 座屈とは 荷重により梁に生じた曲げモーメントをで除して仮想荷重と考える 座屈荷重 偏心荷重 ( 曲げと軸力 ) 断面の核 この仮想荷重に対するある点でのせん断力 たわみ角に相当する曲げモーメント たわみに相当する ( 例 ) 単純梁の支点のたわみ角 : は 図 を仮想荷重と考えたときの 点の支点反力 B は 図 を仮想荷重と考えたときのB
第 回材の座屈 (0 章 ) p.5~ ( 復習 ) モールの定理 ( 手順 ) 座屈とは 荷重により梁に生じた曲げモーメントをで除して仮想荷重と考える 座屈荷重 偏心荷重 ( 曲げと軸力 ) 断面の核 この仮想荷重に対するある点でのせん断力 たわみ角に相当する曲げモーメント たわみに相当する ( 例 ) 単純梁の支点のたわみ角 : は 図 を仮想荷重と考えたときの 点の支点反力 B は 図 を仮想荷重と考えたときのB
Microsoft PowerPoint - H22制御工学I-2回.ppt
 制御工学 I 第二回ラプラス変換 平成 年 4 月 9 日 /4/9 授業の予定 制御工学概論 ( 回 ) 制御技術は現在様々な工学分野において重要な基本技術となっている 工学における制御工学の位置づけと歴史について説明する さらに 制御システムの基本構成と種類を紹介する ラプラス変換 ( 回 ) 制御工学 特に古典制御ではラプラス変換が重要な役割を果たしている ラプラス変換と逆ラプラス変換の定義を紹介し
制御工学 I 第二回ラプラス変換 平成 年 4 月 9 日 /4/9 授業の予定 制御工学概論 ( 回 ) 制御技術は現在様々な工学分野において重要な基本技術となっている 工学における制御工学の位置づけと歴史について説明する さらに 制御システムの基本構成と種類を紹介する ラプラス変換 ( 回 ) 制御工学 特に古典制御ではラプラス変換が重要な役割を果たしている ラプラス変換と逆ラプラス変換の定義を紹介し
Microsoft PowerPoint - 第3回2.ppt
 講義内容 講義内容 次元ベクトル 関数の直交性フーリエ級数 次元代表的な対の諸性質コンボリューション たたみこみ積分 サンプリング定理 次元離散 次元空間周波数の概念 次元代表的な 次元対 次元離散 次元ベクトル 関数の直交性フーリエ級数 次元代表的な対の諸性質コンボリューション たたみこみ積分 サンプリング定理 次元離散 次元空間周波数の概念 次元代表的な 次元対 次元離散 ベクトルの直交性 3
講義内容 講義内容 次元ベクトル 関数の直交性フーリエ級数 次元代表的な対の諸性質コンボリューション たたみこみ積分 サンプリング定理 次元離散 次元空間周波数の概念 次元代表的な 次元対 次元離散 次元ベクトル 関数の直交性フーリエ級数 次元代表的な対の諸性質コンボリューション たたみこみ積分 サンプリング定理 次元離散 次元空間周波数の概念 次元代表的な 次元対 次元離散 ベクトルの直交性 3
ベクトル公式.rtf
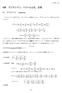 6 章ラプラシアン, ベクトル公式, 定理 6.1 ラプラシアン Laplacian φ はベクトル量である. そこでさらに発散をとると, φ はどういう形になるであろうか? φ = a + a + a φ a + a φ + a φ = φ + φ + φ = 2 φ + 2 φ 2 + 2 φ 2 2 φ = 2 φ 2 + 2 φ 2 + 2 φ 2 = 2 φ したがって,2 階の偏微分演算となる.
6 章ラプラシアン, ベクトル公式, 定理 6.1 ラプラシアン Laplacian φ はベクトル量である. そこでさらに発散をとると, φ はどういう形になるであろうか? φ = a + a + a φ a + a φ + a φ = φ + φ + φ = 2 φ + 2 φ 2 + 2 φ 2 2 φ = 2 φ 2 + 2 φ 2 + 2 φ 2 = 2 φ したがって,2 階の偏微分演算となる.
<4D F736F F D2097CD8A7793FC96E582BD82ED82DD8A E6318FCD2E646F63>
 - 第 章たわみ角法の基本式 ポイント : たわみ角法の基本式を理解する たわみ角法の基本式を梁の微分方程式より求める 本章では たわみ角法の基本式を導くことにする 基本式の誘導法は各種あるが ここでは 梁の微分方程式を解いて基本式を求める方法を採用する この本で使用する座標系は 右手 右ネジの法則に従った座標を用いる また ひとつの部材では 図 - に示すように部材の左端の 点を原点とし 軸線を
- 第 章たわみ角法の基本式 ポイント : たわみ角法の基本式を理解する たわみ角法の基本式を梁の微分方程式より求める 本章では たわみ角法の基本式を導くことにする 基本式の誘導法は各種あるが ここでは 梁の微分方程式を解いて基本式を求める方法を採用する この本で使用する座標系は 右手 右ネジの法則に従った座標を用いる また ひとつの部材では 図 - に示すように部材の左端の 点を原点とし 軸線を
Microsoft Word - thesis.doc
 剛体の基礎理論 -. 剛体の基礎理論初めに本論文で大域的に使用する記号を定義する. 使用する記号トルク撃力力角運動量角速度姿勢対角化された慣性テンソル慣性テンソル運動量速度位置質量時間 J W f F P p .. 質点の並進運動 質点は位置 と速度 P を用いる. ニュートンの運動方程式 という状態を持つ. 但し ここでは速度ではなく運動量 F P F.... より質点の運動は既に明らかであり 質点の状態ベクトル
剛体の基礎理論 -. 剛体の基礎理論初めに本論文で大域的に使用する記号を定義する. 使用する記号トルク撃力力角運動量角速度姿勢対角化された慣性テンソル慣性テンソル運動量速度位置質量時間 J W f F P p .. 質点の並進運動 質点は位置 と速度 P を用いる. ニュートンの運動方程式 という状態を持つ. 但し ここでは速度ではなく運動量 F P F.... より質点の運動は既に明らかであり 質点の状態ベクトル
<4D F736F F D E4F8E9F82C982A882AF82E98D7397F1>
 3 三次における行列 要旨高校では ほとんど 2 2 の正方行列しか扱ってなく 三次の正方行列について考えてみたかったため 数 C で学んだ定理を三次の正方行列に応用して 自分たちで仮説を立てて求めていったら 空間における回転移動を表す行列 三次のケーリー ハミルトンの定理 三次における逆行列を求めたり 仮説をたてることができた. 目的 数 C で学んだ定理を三次の正方行列に応用する 2. 概要目的の到達点として
3 三次における行列 要旨高校では ほとんど 2 2 の正方行列しか扱ってなく 三次の正方行列について考えてみたかったため 数 C で学んだ定理を三次の正方行列に応用して 自分たちで仮説を立てて求めていったら 空間における回転移動を表す行列 三次のケーリー ハミルトンの定理 三次における逆行列を求めたり 仮説をたてることができた. 目的 数 C で学んだ定理を三次の正方行列に応用する 2. 概要目的の到達点として
人間科学部研究年報平成 24 年 (1) (2) (3) (4) 式 (1) は, クーロン (Coulomb) の法則とも呼ばれる.ρは電荷密度を表し,ε 0 は真空の誘電率と呼ばれる定数である. 式 (2) は, 磁荷が存在しないことを表す式である. 式 (3) はファラデー (Faraday)
 複素振幅をもつ球面波の人間科学部研究年報 Maxwell 平成 24 方程式年 複素振幅をもつ球面波の Maxwell 方程式 Maxwell Equation of Spherical Wave with Complex Amplitude 戸上良弘 Yoshihiro TOGAMI Abstract 複素振幅をもつ球面波に関して, マクスウェル (Maxwell) 方程式との関係を考察した. 電気的な球面波としてのスカラーポテンシャルが与えられたとき,
複素振幅をもつ球面波の人間科学部研究年報 Maxwell 平成 24 方程式年 複素振幅をもつ球面波の Maxwell 方程式 Maxwell Equation of Spherical Wave with Complex Amplitude 戸上良弘 Yoshihiro TOGAMI Abstract 複素振幅をもつ球面波に関して, マクスウェル (Maxwell) 方程式との関係を考察した. 電気的な球面波としてのスカラーポテンシャルが与えられたとき,
航空機の運動方程式
 可制御性 可観測性. 可制御性システムの状態を, 適切な操作によって, 有限時間内に, 任意の状態から別の任意の状態に移動させることができるか否かという特性を可制御性という. 可制御性を有するシステムに対し, システムは可制御である, 可制御なシステム という言い方をする. 状態方程式, 出力方程式が以下で表されるn 次元 m 入力 r 出力線形時不変システム x Ax u y x Du () に対し,
可制御性 可観測性. 可制御性システムの状態を, 適切な操作によって, 有限時間内に, 任意の状態から別の任意の状態に移動させることができるか否かという特性を可制御性という. 可制御性を有するシステムに対し, システムは可制御である, 可制御なシステム という言い方をする. 状態方程式, 出力方程式が以下で表されるn 次元 m 入力 r 出力線形時不変システム x Ax u y x Du () に対し,
プランクの公式と量子化
 Planck の公式と量子化 埼玉大学理学部物理学科 久保宗弘 序論 一般に 量子力学 と表現すると Schrödinger の量子力学などの 後期量子力学 を指すことが多い 本当の量子概念 には どうアプローチ? 何故 エネルギーが量子化されるか という根本的な問いにどうこたえるか? どのように 量子 の扉は叩かれたのか? 序論 統計力学 熱力学 がことの始まり 総括的な動き を表現するための学問である
Planck の公式と量子化 埼玉大学理学部物理学科 久保宗弘 序論 一般に 量子力学 と表現すると Schrödinger の量子力学などの 後期量子力学 を指すことが多い 本当の量子概念 には どうアプローチ? 何故 エネルギーが量子化されるか という根本的な問いにどうこたえるか? どのように 量子 の扉は叩かれたのか? 序論 統計力学 熱力学 がことの始まり 総括的な動き を表現するための学問である
Microsoft PowerPoint _量子力学短大.pptx
 . エネルギーギャップとrllouゾーン ブリルアン領域,t_8.. 周期ポテンシャル中の電子とエネルギーギャップ 簡単のため 次元に間隔 で原子が並んでいる結晶を考える 右方向に進行している電子の波は 間隔 で規則正しく並んでいる原子が作る格子によって散乱され 左向きに進行する波となる 波長 λ が の時 r の反射条件 式を満たし 両者の波が互いに強め合い 定在波を作る つまり 式 式を満たす波は
. エネルギーギャップとrllouゾーン ブリルアン領域,t_8.. 周期ポテンシャル中の電子とエネルギーギャップ 簡単のため 次元に間隔 で原子が並んでいる結晶を考える 右方向に進行している電子の波は 間隔 で規則正しく並んでいる原子が作る格子によって散乱され 左向きに進行する波となる 波長 λ が の時 r の反射条件 式を満たし 両者の波が互いに強め合い 定在波を作る つまり 式 式を満たす波は
Microsoft PowerPoint - 第5回電磁気学I
 1 年 11 月 8 日 ( 月 ) 1:-1: Y 平成 年度工 系 ( 社会環境工学科 ) 第 5 回電磁気学 Ⅰ 天野浩 項目 電界と電束密度 ガウスの発散定理とガウスの法則の積分形と微分形 * ファラデーの電気力線の使い方をマスターします * 電界と電束密度を定義します * ガウスの発散定理を用いて ガウスの法則の積分形から微分形をガウスの法則の積分形から微分形を導出します * ガウスの法則を用いて
1 年 11 月 8 日 ( 月 ) 1:-1: Y 平成 年度工 系 ( 社会環境工学科 ) 第 5 回電磁気学 Ⅰ 天野浩 項目 電界と電束密度 ガウスの発散定理とガウスの法則の積分形と微分形 * ファラデーの電気力線の使い方をマスターします * 電界と電束密度を定義します * ガウスの発散定理を用いて ガウスの法則の積分形から微分形をガウスの法則の積分形から微分形を導出します * ガウスの法則を用いて
Microsoft PowerPoint - 10.pptx
 m u. 固有値とその応用 8/7/( 水 ). 固有値とその応用 固有値と固有ベクトル 行列による写像から固有ベクトルへ m m 行列 によって線形写像 f : R R が表せることを見てきた ここでは 次元平面の行列による写像を調べる とし 写像 f : を考える R R まず 単位ベクトルの像 u y y f : R R u u, u この事から 線形写像の性質を用いると 次の格子上の点全ての写像先が求まる
m u. 固有値とその応用 8/7/( 水 ). 固有値とその応用 固有値と固有ベクトル 行列による写像から固有ベクトルへ m m 行列 によって線形写像 f : R R が表せることを見てきた ここでは 次元平面の行列による写像を調べる とし 写像 f : を考える R R まず 単位ベクトルの像 u y y f : R R u u, u この事から 線形写像の性質を用いると 次の格子上の点全ての写像先が求まる
Microsoft PowerPoint - aep_1.ppt [互換モード]
![Microsoft PowerPoint - aep_1.ppt [互換モード] Microsoft PowerPoint - aep_1.ppt [互換モード]](/thumbs/91/107493198.jpg) 物理計測法特論 No.1 第 1 章 : 信号と雑音 本講義の主題 雑音の性質を理解することで 信号と雑音の大きさが非常に近い状態での信号の測定技術 : 微小信号計測 について学ぶ 講義の Web http://www.g-munu.t.u-tokyo.ac.jp/mio/note/sig_mes/tokuron.html 物理学の基本は実験事実の積み重ねである そして それは何かを測定することから始まる
物理計測法特論 No.1 第 1 章 : 信号と雑音 本講義の主題 雑音の性質を理解することで 信号と雑音の大きさが非常に近い状態での信号の測定技術 : 微小信号計測 について学ぶ 講義の Web http://www.g-munu.t.u-tokyo.ac.jp/mio/note/sig_mes/tokuron.html 物理学の基本は実験事実の積み重ねである そして それは何かを測定することから始まる
2 図微小要素の流体の流入出 方向の断面の流体の流入出の収支断面 Ⅰ から微小要素に流入出する流体の流量 Q 断面 Ⅰ は 以下のように定式化できる Q 断面 Ⅰ 流量 密度 流速 断面 Ⅰ の面積 微小要素の断面 Ⅰ から だけ移動した断面 Ⅱ を流入出する流体の流量 Q 断面 Ⅱ は以下のように
 3 章 Web に Link 解説 連続式 微分表示 の誘導.64 *4. 連続式連続式は ある領域の内部にある流体の質量の収支が その表面からの流入出の合計と等しくなることを定式化したものであり 流体における質量保存則を示したものである 2. 連続式 微分表示 の誘導図のような微小要素 コントロールボリューム の領域内の流体の増減と外部からの流体の流入出を考えることで定式化できる 微小要素 流入
3 章 Web に Link 解説 連続式 微分表示 の誘導.64 *4. 連続式連続式は ある領域の内部にある流体の質量の収支が その表面からの流入出の合計と等しくなることを定式化したものであり 流体における質量保存則を示したものである 2. 連続式 微分表示 の誘導図のような微小要素 コントロールボリューム の領域内の流体の増減と外部からの流体の流入出を考えることで定式化できる 微小要素 流入
<4D F736F F D20824F F6490CF95AA82C696CA90CF95AA2E646F63>
 1/15 平成 3 年 3 月 4 日午後 6 時 49 分 5 ベクトルの 重積分と面積分 5 重積分と面積分 Ⅰ. 重積分 と で 回積分することを 重積分 といいます この 重積分は何を意味しているのでしょう? 通常の積分 (1 重積分 ) では C d 図 1a 1 f d (5.1) 1 f d f ( ) は 図形的には図 1a のように面積を表しています つまり 1 f ( ) を高さとしてプロットすると図
1/15 平成 3 年 3 月 4 日午後 6 時 49 分 5 ベクトルの 重積分と面積分 5 重積分と面積分 Ⅰ. 重積分 と で 回積分することを 重積分 といいます この 重積分は何を意味しているのでしょう? 通常の積分 (1 重積分 ) では C d 図 1a 1 f d (5.1) 1 f d f ( ) は 図形的には図 1a のように面積を表しています つまり 1 f ( ) を高さとしてプロットすると図
工業数学F2-04(ウェブ用).pptx
 工業数学 F2 #4 フーリエ級数を極める 京都大学加納学 京都大学大学院情報学研究科システム科学専攻 Human Systems Lab., Dept. of Systems Science Graduate School of Informatics, Kyoto University 復習 1: 複素フーリエ級数 2 周期 2π の周期関数 f(x) の複素フーリエ級数展開 複素フーリエ係数
工業数学 F2 #4 フーリエ級数を極める 京都大学加納学 京都大学大学院情報学研究科システム科学専攻 Human Systems Lab., Dept. of Systems Science Graduate School of Informatics, Kyoto University 復習 1: 複素フーリエ級数 2 周期 2π の周期関数 f(x) の複素フーリエ級数展開 複素フーリエ係数
2011年度 大阪大・理系数学
 0 大阪大学 ( 理系 ) 前期日程問題 解答解説のページへ a a を自然数とする O を原点とする座標平面上で行列 A= a の表す 次変換 を f とする cosθ siθ () >0 および0θ
0 大阪大学 ( 理系 ) 前期日程問題 解答解説のページへ a a を自然数とする O を原点とする座標平面上で行列 A= a の表す 次変換 を f とする cosθ siθ () >0 および0θ
Microsoft Word - 中村工大連携教材(最終 ).doc
 音速について考えてみよう! 金沢工業大学 中村晃 ねらい 私たちの身の回りにはいろいろな種類の波が存在する. 体感できる波もあれば, できない波もある. その中で音は体感できる最も身近な波である. 遠くで雷が光ってから雷鳴が届くまで数秒間時間がかかることにより, 音の方が光より伝わるのに時間がかかることも経験していると思う. 高校の物理の授業で音の伝わる速さ ( 音速 ) は約 m/s で, 詳しく述べると
音速について考えてみよう! 金沢工業大学 中村晃 ねらい 私たちの身の回りにはいろいろな種類の波が存在する. 体感できる波もあれば, できない波もある. その中で音は体感できる最も身近な波である. 遠くで雷が光ってから雷鳴が届くまで数秒間時間がかかることにより, 音の方が光より伝わるのに時間がかかることも経験していると思う. 高校の物理の授業で音の伝わる速さ ( 音速 ) は約 m/s で, 詳しく述べると
( 慣性抵抗 ) 速度の 2 乗に比例流体中を進む物体は前面にある流体を押しのけて進む. 物 aaa 体の後面には流体が付き従う ( 渦を巻いて ). 前面にある速度 0 の流体が後面に移動して速度 vとなったと考えてよい. この流体の質量は単位時間内に物体が押しのける体積に比例するので,v に比例
 空気抵抗があるときの自由落下 抵抗が速度に比例する場合 1. 絵を描く, 座標と情報, 記号を記入する x F0 v
空気抵抗があるときの自由落下 抵抗が速度に比例する場合 1. 絵を描く, 座標と情報, 記号を記入する x F0 v
Microsoft Word - mathtext8.doc
 8 章偏微分と重積分 8. 偏微分とは これまで微分を考える際 関数は f という形で 関数値がつの変数 に依存している場合のみを扱ってきました しかし一般に変数はつとは決まっておらず f のように 複数の変数を持つ関数も考えなければなりません そ こでこの節では今まで学んできた微分を一般化させ 複数の変数に対応した偏微分と呼ばれるものについて説明します これまでの微分を偏微分と区別したいとき 常微分という呼び方を用います
8 章偏微分と重積分 8. 偏微分とは これまで微分を考える際 関数は f という形で 関数値がつの変数 に依存している場合のみを扱ってきました しかし一般に変数はつとは決まっておらず f のように 複数の変数を持つ関数も考えなければなりません そ こでこの節では今まで学んできた微分を一般化させ 複数の変数に対応した偏微分と呼ばれるものについて説明します これまでの微分を偏微分と区別したいとき 常微分という呼び方を用います
1/30 平成 29 年 3 月 24 日 ( 金 ) 午前 11 時 25 分第三章フェルミ量子場 : スピノール場 ( 次元あり ) 第三章フェルミ量子場 : スピノール場 フェルミ型 ボーズ量子場のエネルギーは 第二章ボーズ量子場 : スカラー場 の (2.18) より ˆ dp 1 1 =
 / 平成 9 年 月 日 ( 金 午前 時 5 分第三章フェルミ量子場 : スピノール場 ( 次元あり 第三章フェルミ量子場 : スピノール場 フェルミ型 ボーズ量子場のエネルギーは 第二章ボーズ量子場 : スカラー場 の (.8 より ˆ ( ( ( q -, ( ( c ( H c c ë é ù û - Ü + c ( ( - に限る (. である 一方 フェルミ型は 成分をもち その成分を,,,,
/ 平成 9 年 月 日 ( 金 午前 時 5 分第三章フェルミ量子場 : スピノール場 ( 次元あり 第三章フェルミ量子場 : スピノール場 フェルミ型 ボーズ量子場のエネルギーは 第二章ボーズ量子場 : スカラー場 の (.8 より ˆ ( ( ( q -, ( ( c ( H c c ë é ù û - Ü + c ( ( - に限る (. である 一方 フェルミ型は 成分をもち その成分を,,,,
座標系.rtf
 2 章座標系 場 空間は3 次元なので, ベクトルを表現するには少なくとも3 成分を指定する必要がある. そのために座標系が必要となる. 座標系として最も一般的なものは,,, 成分を使った直角座標系である. しかし, 他にも円柱座標, 球座標, だ円座標, 放物線座標など様々なものがある. 現在までに3 成分で変数分離可能な座標系は11 個あるといわれている (Moon & Spencer, Field
2 章座標系 場 空間は3 次元なので, ベクトルを表現するには少なくとも3 成分を指定する必要がある. そのために座標系が必要となる. 座標系として最も一般的なものは,,, 成分を使った直角座標系である. しかし, 他にも円柱座標, 球座標, だ円座標, 放物線座標など様々なものがある. 現在までに3 成分で変数分離可能な座標系は11 個あるといわれている (Moon & Spencer, Field
Laplace2.rtf
 =0 ラプラスの方程式は 階の微分方程式で, 一般的に3つの座標変数をもつ. ここでは, 直角座標系, 円筒座標系, 球座標系におけるラプラスの方程式の解き方を説明しよう. 座標変数ごとに方程式を分離し, それを解いていく方法は変数分離法と呼ばれる. 変数分離解と固有関数展開法. 直角座標系における 3 次元の偏微分方程式 = x + y + z =0 (.) を解くために,x, y, z について互いに独立な関数の積で成り立っていると考え,
=0 ラプラスの方程式は 階の微分方程式で, 一般的に3つの座標変数をもつ. ここでは, 直角座標系, 円筒座標系, 球座標系におけるラプラスの方程式の解き方を説明しよう. 座標変数ごとに方程式を分離し, それを解いていく方法は変数分離法と呼ばれる. 変数分離解と固有関数展開法. 直角座標系における 3 次元の偏微分方程式 = x + y + z =0 (.) を解くために,x, y, z について互いに独立な関数の積で成り立っていると考え,
喨微勃挹稉弑
 == 全微分方程式 == 全微分とは 変数の関数 z=f(, ) について,, の増分を Δ, Δ とするとき, z の増分 Δz は Δz z Δ+ z Δ で表されます. この式において, Δ 0, Δ 0 となる極限を形式的に dz= z d+ z d (1) で表し, dz を z の全微分といいます. z は z の に関する偏導関数で, を定数と見なし て, で微分したものを表し, 方向の傾きに対応します.
== 全微分方程式 == 全微分とは 変数の関数 z=f(, ) について,, の増分を Δ, Δ とするとき, z の増分 Δz は Δz z Δ+ z Δ で表されます. この式において, Δ 0, Δ 0 となる極限を形式的に dz= z d+ z d (1) で表し, dz を z の全微分といいます. z は z の に関する偏導関数で, を定数と見なし て, で微分したものを表し, 方向の傾きに対応します.
数学 ⅡB < 公理 > 公理を論拠に定義を用いて定理を証明する 1 大小関係の公理 順序 (a > b, a = b, a > b 1 つ成立 a > b, b > c a > c 成立 ) 順序と演算 (a > b a + c > b + c (a > b, c > 0 ac > bc) 2 図
 数学 Ⅱ < 公理 > 公理を論拠に定義を用いて定理を証明する 大小関係の公理 順序 >, =, > つ成立 >, > > 成立 順序と演算 > + > + >, > > 図形の公理 平行線の性質 錯角 同位角 三角形の合同条件 三角形の合同相似 量の公理 角の大きさ 線分の長さ < 空間における座漂とベクトル > ベクトルの演算 和 差 実数倍については 文字の計算と同様 ベクトルの成分表示 平面ベクトル
数学 Ⅱ < 公理 > 公理を論拠に定義を用いて定理を証明する 大小関係の公理 順序 >, =, > つ成立 >, > > 成立 順序と演算 > + > + >, > > 図形の公理 平行線の性質 錯角 同位角 三角形の合同条件 三角形の合同相似 量の公理 角の大きさ 線分の長さ < 空間における座漂とベクトル > ベクトルの演算 和 差 実数倍については 文字の計算と同様 ベクトルの成分表示 平面ベクトル
PowerPoint Presentation
 Non-linea factue mechanics き裂先端付近の塑性変形 塑性域 R 破壊進行領域応カ特異場 Ω R R Hutchinson, Rice and Rosengen 全ひずみ塑性理論に基づいた解析 現段階のひずみは 除荷がないとすると現段階の応力で一義的に決まる 単純引張り時の応カーひずみ関係 ( 構成方程式 ): ( ) ( ) n () y y y ここで α,n 定数, /
Non-linea factue mechanics き裂先端付近の塑性変形 塑性域 R 破壊進行領域応カ特異場 Ω R R Hutchinson, Rice and Rosengen 全ひずみ塑性理論に基づいた解析 現段階のひずみは 除荷がないとすると現段階の応力で一義的に決まる 単純引張り時の応カーひずみ関係 ( 構成方程式 ): ( ) ( ) n () y y y ここで α,n 定数, /
DVIOUT
 第 章 離散フーリエ変換 離散フーリエ変換 これまで 私たちは連続関数に対するフーリエ変換およびフーリエ積分 ( 逆フーリエ変換 ) について学んできました この節では フーリエ変換を離散化した離散フーリエ変換について学びましょう 自然現象 ( 音声 ) などを観測して得られる波 ( 信号値 ; 観測値 ) は 通常 電気信号による連続的な波として観測機器から出力されます しかしながら コンピュータはこの様な連続的な波を直接扱うことができないため
第 章 離散フーリエ変換 離散フーリエ変換 これまで 私たちは連続関数に対するフーリエ変換およびフーリエ積分 ( 逆フーリエ変換 ) について学んできました この節では フーリエ変換を離散化した離散フーリエ変換について学びましょう 自然現象 ( 音声 ) などを観測して得られる波 ( 信号値 ; 観測値 ) は 通常 電気信号による連続的な波として観測機器から出力されます しかしながら コンピュータはこの様な連続的な波を直接扱うことができないため
DVIOUT
 最適レギュレータ 松尾研究室資料 第 最適レギュレータ 節時不変型無限時間最適レギュレータ 状態フィードバックの可能な場合の無限時間問題における最適レギュレータについて確定系について説明する. ここで, レギュレータとは状態量をゼロにするようなコントローラのことである. なぜ, 無限時間問題のみを述べるかという理由は以下のとおりである. 有限時間の最適レギュレータ問題の場合の最適フィードバックゲインは微分方程式の解から構成される時間関数として表現される.
最適レギュレータ 松尾研究室資料 第 最適レギュレータ 節時不変型無限時間最適レギュレータ 状態フィードバックの可能な場合の無限時間問題における最適レギュレータについて確定系について説明する. ここで, レギュレータとは状態量をゼロにするようなコントローラのことである. なぜ, 無限時間問題のみを述べるかという理由は以下のとおりである. 有限時間の最適レギュレータ問題の場合の最適フィードバックゲインは微分方程式の解から構成される時間関数として表現される.
モデリングとは
 コンピュータグラフィックス基礎 第 5 回曲線 曲面の表現 ベジェ曲線 金森由博 学習の目標 滑らかな曲線を扱う方法を学習する パラメトリック曲線について理解する 広く一般的に使われているベジェ曲線を理解する 制御点を入力することで ベジェ曲線を描画するアプリケーションの開発を行えるようになる C++ 言語の便利な機能を使えるようになる 要素数が可変な配列としての std::vector の活用 計算機による曲線の表現
コンピュータグラフィックス基礎 第 5 回曲線 曲面の表現 ベジェ曲線 金森由博 学習の目標 滑らかな曲線を扱う方法を学習する パラメトリック曲線について理解する 広く一般的に使われているベジェ曲線を理解する 制御点を入力することで ベジェ曲線を描画するアプリケーションの開発を行えるようになる C++ 言語の便利な機能を使えるようになる 要素数が可変な配列としての std::vector の活用 計算機による曲線の表現
Microsoft PowerPoint - mp11-02.pptx
 数理計画法第 2 回 塩浦昭義情報科学研究科准教授 shioura@dais.is.tohoku.ac.jp http://www.dais.is.tohoku.ac.jp/~shioura/teaching 前回の復習 数理計画とは? 数理計画 ( 復習 ) 数理計画問題とは? 狭義には : 数理 ( 数学 ) を使って計画を立てるための問題 広義には : 与えられた評価尺度に関して最も良い解を求める問題
数理計画法第 2 回 塩浦昭義情報科学研究科准教授 shioura@dais.is.tohoku.ac.jp http://www.dais.is.tohoku.ac.jp/~shioura/teaching 前回の復習 数理計画とは? 数理計画 ( 復習 ) 数理計画問題とは? 狭義には : 数理 ( 数学 ) を使って計画を立てるための問題 広義には : 与えられた評価尺度に関して最も良い解を求める問題
Microsoft PowerPoint - CSA_B3_EX2.pptx
 Computer Science A Hardware Design Excise 2 Handout V2.01 May 27 th.,2019 CSAHW Computer Science A, Meiji University CSA_B3_EX2.pptx 32 Slides Renji Mikami 1 CSAHW2 ハード演習内容 2.1 二次元空間でのベクトルの直交 2.2 Reserved
Computer Science A Hardware Design Excise 2 Handout V2.01 May 27 th.,2019 CSAHW Computer Science A, Meiji University CSA_B3_EX2.pptx 32 Slides Renji Mikami 1 CSAHW2 ハード演習内容 2.1 二次元空間でのベクトルの直交 2.2 Reserved
Microsoft PowerPoint - zairiki_3
 材料力学講義 (3) 応力と変形 Ⅲ ( 曲げモーメント, 垂直応力度, 曲率 ) 今回は, 曲げモーメントに関する, 断面力 - 応力度 - 変形 - 変位の関係について学びます 1 曲げモーメント 曲げモーメント M 静定力学で求めた曲げモーメントも, 仮想的に断面を切ることによって現れる内力です 軸方向力は断面に働く力 曲げモーメント M は断面力 曲げモーメントも, 一つのモーメントとして表しますが,
材料力学講義 (3) 応力と変形 Ⅲ ( 曲げモーメント, 垂直応力度, 曲率 ) 今回は, 曲げモーメントに関する, 断面力 - 応力度 - 変形 - 変位の関係について学びます 1 曲げモーメント 曲げモーメント M 静定力学で求めた曲げモーメントも, 仮想的に断面を切ることによって現れる内力です 軸方向力は断面に働く力 曲げモーメント M は断面力 曲げモーメントも, 一つのモーメントとして表しますが,
Microsoft PowerPoint - ip02_01.ppt [互換モード]
![Microsoft PowerPoint - ip02_01.ppt [互換モード] Microsoft PowerPoint - ip02_01.ppt [互換モード]](/thumbs/96/127250376.jpg) 空間周波数 周波数領域での処理 空間周波数 (spatial frquncy) とは 単位長さ当たりの正弦波状の濃淡変化の繰り返し回数を表したもの 正弦波 : y sin( t) 周期 : 周波数 : T f / T 角周波数 : f 画像処理 空間周波数 周波数領域での処理 波形が違うと 周波数も違う 画像処理 空間周波数 周波数領域での処理 画像処理 3 周波数領域での処理 周波数は一つしかない?-
空間周波数 周波数領域での処理 空間周波数 (spatial frquncy) とは 単位長さ当たりの正弦波状の濃淡変化の繰り返し回数を表したもの 正弦波 : y sin( t) 周期 : 周波数 : T f / T 角周波数 : f 画像処理 空間周波数 周波数領域での処理 波形が違うと 周波数も違う 画像処理 空間周波数 周波数領域での処理 画像処理 3 周波数領域での処理 周波数は一つしかない?-
Microsoft Word - note02.doc
 年度 物理化学 Ⅱ 講義ノート. 二原子分子の振動. 調和振動子近似 モデル 分子 = 理想的なバネでつながった原子 r : 核間距離, r e : 平衡核間距離, : 変位 ( = r r e ), k f : 力の定数ポテンシャルエネルギー ( ) k V = f (.) 古典運動方程式 [ 振動数 ] 3.3 d kf (.) dt μ : 換算質量 (m, m : 原子, の質量 ) mm
年度 物理化学 Ⅱ 講義ノート. 二原子分子の振動. 調和振動子近似 モデル 分子 = 理想的なバネでつながった原子 r : 核間距離, r e : 平衡核間距離, : 変位 ( = r r e ), k f : 力の定数ポテンシャルエネルギー ( ) k V = f (.) 古典運動方程式 [ 振動数 ] 3.3 d kf (.) dt μ : 換算質量 (m, m : 原子, の質量 ) mm
Microsoft PowerPoint - 9.pptx
 9. 線形写像 ここでは 行列の積によって 写像を定義できることをみていく また 行列の積によって定義される写像の性質を調べていく 行列演算と写像 ( 次変換 3 拡大とスカラー倍 p ' = ( ', ' = ( k, kk p = (, k 倍 k 倍 拡大後 k 倍拡大の関係は スカラー倍を用いて次のように表現できる ' = k ' 拡大前 拡大 4 拡大と行列の積 p ' = ( ', '
9. 線形写像 ここでは 行列の積によって 写像を定義できることをみていく また 行列の積によって定義される写像の性質を調べていく 行列演算と写像 ( 次変換 3 拡大とスカラー倍 p ' = ( ', ' = ( k, kk p = (, k 倍 k 倍 拡大後 k 倍拡大の関係は スカラー倍を用いて次のように表現できる ' = k ' 拡大前 拡大 4 拡大と行列の積 p ' = ( ', '
画像処理工学
 画像処理工学 画像の空間周波数解析とテクスチャ特徴 フーリエ変換の基本概念 信号波形のフーリエ変換 信号波形を周波数の異なる三角関数 ( 正弦波など ) に分解する 逆に, 周波数の異なる三角関数を重ねあわせることにより, 任意の信号波形を合成できる 正弦波の重ね合わせによる矩形波の表現 フーリエ変換の基本概念 フーリエ変換 次元信号 f (t) のフーリエ変換 変換 ( ω) ( ) ωt F f
画像処理工学 画像の空間周波数解析とテクスチャ特徴 フーリエ変換の基本概念 信号波形のフーリエ変換 信号波形を周波数の異なる三角関数 ( 正弦波など ) に分解する 逆に, 周波数の異なる三角関数を重ねあわせることにより, 任意の信号波形を合成できる 正弦波の重ね合わせによる矩形波の表現 フーリエ変換の基本概念 フーリエ変換 次元信号 f (t) のフーリエ変換 変換 ( ω) ( ) ωt F f
Microsoft Word - 微分入門.doc
 基本公式 例題 0 定義式 f( ) 数 Ⅲ 微分入門 = の導関数を定義式にもとづいて計算しなさい 基本事項 ( f( ), g( ) が微分可能ならば ) y= f( ) g( ) のとき, y = y= f( ) g( ) h( ) のとき, y = ( f( ), g( ) が微分可能で, g( ) 0 ならば ) f( ) y = のとき, y = g ( ) とくに, y = のとき,
基本公式 例題 0 定義式 f( ) 数 Ⅲ 微分入門 = の導関数を定義式にもとづいて計算しなさい 基本事項 ( f( ), g( ) が微分可能ならば ) y= f( ) g( ) のとき, y = y= f( ) g( ) h( ) のとき, y = ( f( ), g( ) が微分可能で, g( ) 0 ならば ) f( ) y = のとき, y = g ( ) とくに, y = のとき,
様々なミクロ計量モデル†
 担当 : 長倉大輔 ( ながくらだいすけ ) この資料は私の講義において使用するために作成した資料です WEB ページ上で公開しており 自由に参照して頂いて構いません ただし 内容について 一応検証してありますが もし間違いがあった場合でもそれによって生じるいかなる損害 不利益について責任を負いかねますのでご了承ください 間違いは発見次第 継続的に直していますが まだ存在する可能性があります 1 カウントデータモデル
担当 : 長倉大輔 ( ながくらだいすけ ) この資料は私の講義において使用するために作成した資料です WEB ページ上で公開しており 自由に参照して頂いて構いません ただし 内容について 一応検証してありますが もし間違いがあった場合でもそれによって生じるいかなる損害 不利益について責任を負いかねますのでご了承ください 間違いは発見次第 継続的に直していますが まだ存在する可能性があります 1 カウントデータモデル
Microsoft Word - NumericalComputation.docx
 数値計算入門 武尾英哉. 離散数学と数値計算 数学的解法の中には理論計算では求められないものもある. 例えば, 定積分は, まずは積分 ( 被積分関数の原始関数をみつけること できなければ値を得ることはできない. また, ある関数の所定の値における微分値を得るには, まずその関数の微分ができなければならない. さらに代数方程式の解を得るためには, 解析的に代数方程式を解く必要がある. ところが, これらは必ずしも解析的に導けるとは限らない.
数値計算入門 武尾英哉. 離散数学と数値計算 数学的解法の中には理論計算では求められないものもある. 例えば, 定積分は, まずは積分 ( 被積分関数の原始関数をみつけること できなければ値を得ることはできない. また, ある関数の所定の値における微分値を得るには, まずその関数の微分ができなければならない. さらに代数方程式の解を得るためには, 解析的に代数方程式を解く必要がある. ところが, これらは必ずしも解析的に導けるとは限らない.
2018年度 東京大・理系数学
 08 東京大学 ( 理系 ) 前期日程問題 解答解説のページへ関数 f ( ) = + cos (0 < < ) の増減表をつくり, + 0, 0 のと sin きの極限を調べよ 08 東京大学 ( 理系 ) 前期日程問題 解答解説のページへ n+ 数列 a, a, を, Cn a n = ( n =,, ) で定める n! an qn () n とする を既約分数 an p として表したときの分母
08 東京大学 ( 理系 ) 前期日程問題 解答解説のページへ関数 f ( ) = + cos (0 < < ) の増減表をつくり, + 0, 0 のと sin きの極限を調べよ 08 東京大学 ( 理系 ) 前期日程問題 解答解説のページへ n+ 数列 a, a, を, Cn a n = ( n =,, ) で定める n! an qn () n とする を既約分数 an p として表したときの分母
横浜市環境科学研究所
 周期時系列の統計解析 単回帰分析 io 8 年 3 日 周期時系列に季節調整を行わないで単回帰分析を適用すると, 回帰係数には周期成分の影響が加わる. ここでは, 周期時系列をコサイン関数モデルで近似し単回帰分析によりモデルの回帰係数を求め, 周期成分の影響を検討した. また, その結果を気温時系列に当てはめ, 課題等について考察した. 気温時系列とコサイン関数モデル第 報の結果を利用するので, その一部を再掲する.
周期時系列の統計解析 単回帰分析 io 8 年 3 日 周期時系列に季節調整を行わないで単回帰分析を適用すると, 回帰係数には周期成分の影響が加わる. ここでは, 周期時系列をコサイン関数モデルで近似し単回帰分析によりモデルの回帰係数を求め, 周期成分の影響を検討した. また, その結果を気温時系列に当てはめ, 課題等について考察した. 気温時系列とコサイン関数モデル第 報の結果を利用するので, その一部を再掲する.
補足 中学で学習したフレミング左手の法則 ( 電 磁 力 ) と関連付けると覚えやすい 電磁力は電流と磁界の外積で表される 力 F 磁 電磁力 F li 右ねじの回転の向き電 li ( l は導線の長さ ) 補足 有向線分とベクトル有向線分 : 矢印の位
 http://totemt.sur.ne.p 外積 ( ベクトル積 ) の活用 ( 面積, 法線ベクトル, 平面の方程式 ) 3 次元空間の つのベクトルの積が つのベクトルを与えるようなベクトルの掛け算 ベクトルの積がベクトルを与えることからベクトル積とも呼ばれる これに対し内積は符号と大きさをもつ量 ( スカラー量 ) を与えるので, スカラー積とも呼ばれる 外積を使うと, 平行四辺形や三角形の面積,
http://totemt.sur.ne.p 外積 ( ベクトル積 ) の活用 ( 面積, 法線ベクトル, 平面の方程式 ) 3 次元空間の つのベクトルの積が つのベクトルを与えるようなベクトルの掛け算 ベクトルの積がベクトルを与えることからベクトル積とも呼ばれる これに対し内積は符号と大きさをもつ量 ( スカラー量 ) を与えるので, スカラー積とも呼ばれる 外積を使うと, 平行四辺形や三角形の面積,
第6章 実験モード解析
 第 6 章実験モード解析 6. 実験モード解析とは 6. 有限自由度系の実験モード解析 6.3 連続体の実験モード解析 6. 実験モード解析とは 実験モード解析とは加振実験によって測定された外力と応答を用いてモードパラメータ ( 固有振動数, モード減衰比, 正規固有モードなど ) を求める ( 同定する ) 方法である. 力計 試験体 変位計 / 加速度計 実験モード解析の概念 時間領域データを利用する方法
第 6 章実験モード解析 6. 実験モード解析とは 6. 有限自由度系の実験モード解析 6.3 連続体の実験モード解析 6. 実験モード解析とは 実験モード解析とは加振実験によって測定された外力と応答を用いてモードパラメータ ( 固有振動数, モード減衰比, 正規固有モードなど ) を求める ( 同定する ) 方法である. 力計 試験体 変位計 / 加速度計 実験モード解析の概念 時間領域データを利用する方法
2016年度 筑波大・理系数学
 06 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ k を実数とする y 平面の曲線 C : y とC : y- + k+ -k が異なる共 有点 P, Q をもつとする ただし点 P, Q の 座標は正であるとする また, 原点を O とする () k のとりうる値の範囲を求めよ () k が () の範囲を動くとき, OPQ の重心 G の軌跡を求めよ () OPQ の面積を S とするとき,
06 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ k を実数とする y 平面の曲線 C : y とC : y- + k+ -k が異なる共 有点 P, Q をもつとする ただし点 P, Q の 座標は正であるとする また, 原点を O とする () k のとりうる値の範囲を求めよ () k が () の範囲を動くとき, OPQ の重心 G の軌跡を求めよ () OPQ の面積を S とするとき,
反射係数
 平面波の反射と透過 電磁波の性質として, 反射と透過は最も基礎的な現象である. 我々の生活している空間は, 各種の形状を持った媒質で構成されている. 人間から見れば, 空気, 水, 木, 土, 火, 金属, プラスチックなど, 全く異なるものに見えるが, 電磁波からすると誘電率, 透磁率, 導電率が異なるだけである. 磁性体を除く媒質は比透磁率がで, ほとんど媒質に当てはまるので, 実質的に我々の身の回りの媒質で,
平面波の反射と透過 電磁波の性質として, 反射と透過は最も基礎的な現象である. 我々の生活している空間は, 各種の形状を持った媒質で構成されている. 人間から見れば, 空気, 水, 木, 土, 火, 金属, プラスチックなど, 全く異なるものに見えるが, 電磁波からすると誘電率, 透磁率, 導電率が異なるだけである. 磁性体を除く媒質は比透磁率がで, ほとんど媒質に当てはまるので, 実質的に我々の身の回りの媒質で,
Microsoft PowerPoint - 複素数.pptx
 00 年 月 9 日 ( 金 第 時限 平成 年度物質科学解析第 7 回 複素数 冨田知志 0. なぜ複素数か?. 虚数単位. 複素数の計算. オイラーの公式. 複素平面 5. 級数での複素数 ( オイラーの公式 の活用 6. 量子力学で出てくる複素数の例 0. なぜ複素数か? 量子論 ( 量子力学 で不可欠だから参照 : 光ナノサイエンスコアI 古典論や電気回路でも複素数は使うただしそれはあくまでも数学的道具
00 年 月 9 日 ( 金 第 時限 平成 年度物質科学解析第 7 回 複素数 冨田知志 0. なぜ複素数か?. 虚数単位. 複素数の計算. オイラーの公式. 複素平面 5. 級数での複素数 ( オイラーの公式 の活用 6. 量子力学で出てくる複素数の例 0. なぜ複素数か? 量子論 ( 量子力学 で不可欠だから参照 : 光ナノサイエンスコアI 古典論や電気回路でも複素数は使うただしそれはあくまでも数学的道具
物性基礎
 水素様原子 水素原子 水素様原子 エネルギー固有値 波動関数 主量子数 角運動量 方位量子数 磁気量子数 原子核 + 電子 個 F p F = V = 水素様原子 古典力学 水素様原子 量子力学 角運動量 L p F p L 運動方程式 d dt p = d d d p p = p + dt dt dt = p p = d dt L = 角運動量の保存則 ポテンシャルエネルギー V = 4πε =
水素様原子 水素原子 水素様原子 エネルギー固有値 波動関数 主量子数 角運動量 方位量子数 磁気量子数 原子核 + 電子 個 F p F = V = 水素様原子 古典力学 水素様原子 量子力学 角運動量 L p F p L 運動方程式 d dt p = d d d p p = p + dt dt dt = p p = d dt L = 角運動量の保存則 ポテンシャルエネルギー V = 4πε =
ハートレー近似(Hartree aproximation)
 ハートリー近似 ( 量子多体系の平均場近似 1) 0. ハミルトニアンの期待値の変分がシュレディンガー方程式と等価であること 1. 独立粒子近似という考え方. 電子系におけるハートリー近似 3.3 電子系におけるハートリー近似 Mde by R. Okmoto (Kyushu Institute of Technology) filenme=rtree080609.ppt (0) ハミルトニアンの期待値の変分と
ハートリー近似 ( 量子多体系の平均場近似 1) 0. ハミルトニアンの期待値の変分がシュレディンガー方程式と等価であること 1. 独立粒子近似という考え方. 電子系におけるハートリー近似 3.3 電子系におけるハートリー近似 Mde by R. Okmoto (Kyushu Institute of Technology) filenme=rtree080609.ppt (0) ハミルトニアンの期待値の変分と
Microsoft PowerPoint - 9.pptx
 9/7/8( 水 9. 線形写像 ここでは 行列の積によって 写像を定義できることをみていく また 行列の積によって定義される写像の性質を調べていく 拡大とスカラー倍 行列演算と写像 ( 次変換 拡大後 k 倍 k 倍 k 倍拡大の関係は スカラー倍を用いて次のように表現できる p = (, ' = k ' 拡大前 p ' = ( ', ' = ( k, k 拡大 4 拡大と行列の積 拡大後 k 倍
9/7/8( 水 9. 線形写像 ここでは 行列の積によって 写像を定義できることをみていく また 行列の積によって定義される写像の性質を調べていく 拡大とスカラー倍 行列演算と写像 ( 次変換 拡大後 k 倍 k 倍 k 倍拡大の関係は スカラー倍を用いて次のように表現できる p = (, ' = k ' 拡大前 p ' = ( ', ' = ( k, k 拡大 4 拡大と行列の積 拡大後 k 倍
コンピュータグラフィックス第8回
 コンピュータグラフィックス 第 8 回 レンダリング技法 1 ~ 基礎と概要, 隠面消去 ~ 理工学部 兼任講師藤堂英樹 レポート提出状況 課題 1 の選択が多い (STAND BY ME ドラえもん ) 体験演習型 ( 課題 3, 課題 4) の選択も多い 内訳 課題 1 課題 2 課題 3 課題 4 課題 5 2014/11/24 コンピュータグラフィックス 2 次回レポートの体験演習型 メタセコイア,
コンピュータグラフィックス 第 8 回 レンダリング技法 1 ~ 基礎と概要, 隠面消去 ~ 理工学部 兼任講師藤堂英樹 レポート提出状況 課題 1 の選択が多い (STAND BY ME ドラえもん ) 体験演習型 ( 課題 3, 課題 4) の選択も多い 内訳 課題 1 課題 2 課題 3 課題 4 課題 5 2014/11/24 コンピュータグラフィックス 2 次回レポートの体験演習型 メタセコイア,
1/12 平成 29 年 3 月 24 日午後 1 時 1 分第 3 章測地線 第 3 章測地線 Ⅰ. 変分法と運動方程式最小作用の原理に基づくラグランジュの方法により 重力場中の粒子の運動方程式が求められる これは 力が未知の時に有効な方法であり 今のような 一般相対性理論における力を求めるのに使
 / 平成 9 年 3 月 4 日午後 時 分第 3 章測地線 第 3 章測地線 Ⅰ. 変分法と運動方程式最小作用の原理に基づくラグランジュの方法により 重力場中の粒子の運動方程式が求められる これは 力が未知の時に有効な方法であり 今のような 一般相対性理論における力を求めるのに使う事ができる 最小作用の原理 : 粒子が時刻 から の間に移動したとき 位置 と速度 v = するのが ラグランジュ関数
/ 平成 9 年 3 月 4 日午後 時 分第 3 章測地線 第 3 章測地線 Ⅰ. 変分法と運動方程式最小作用の原理に基づくラグランジュの方法により 重力場中の粒子の運動方程式が求められる これは 力が未知の時に有効な方法であり 今のような 一般相対性理論における力を求めるのに使う事ができる 最小作用の原理 : 粒子が時刻 から の間に移動したとき 位置 と速度 v = するのが ラグランジュ関数
Microsoft PowerPoint - 第7章(自然対流熱伝達 )_H27.ppt [互換モード]
![Microsoft PowerPoint - 第7章(自然対流熱伝達 )_H27.ppt [互換モード] Microsoft PowerPoint - 第7章(自然対流熱伝達 )_H27.ppt [互換モード]](/thumbs/94/118222251.jpg) 第 7 章自然対流熱伝達 伝熱工学の基礎 : 伝熱の基本要素 フーリエの法則 ニュートンの冷却則 次元定常熱伝導 : 熱伝導率 熱通過率 熱伝導方程式 次元定常熱伝導 : ラプラスの方程式 数値解析の基礎 非定常熱伝導 : 非定常熱伝導方程式 ラプラス変換 フーリエ数とビオ数 対流熱伝達の基礎 : 熱伝達率 速度境界層と温度境界層 層流境界層と乱流境界層 境界層厚さ 混合平均温度 強制対流熱伝達 :
第 7 章自然対流熱伝達 伝熱工学の基礎 : 伝熱の基本要素 フーリエの法則 ニュートンの冷却則 次元定常熱伝導 : 熱伝導率 熱通過率 熱伝導方程式 次元定常熱伝導 : ラプラスの方程式 数値解析の基礎 非定常熱伝導 : 非定常熱伝導方程式 ラプラス変換 フーリエ数とビオ数 対流熱伝達の基礎 : 熱伝達率 速度境界層と温度境界層 層流境界層と乱流境界層 境界層厚さ 混合平均温度 強制対流熱伝達 :
スライド 1
 非線形数理秋の学校 パターン形成の数理とその周辺 - 反応拡散方程式理論による時 空間パターンの解析を中心に - 2007 年 9 月 25 日 -27 日 モデル方程式を通してみるパターン解析ー進行波からヘリカル波の分岐を例としてー 池田勉 ( 龍谷大学理工学部 ) 講義概要, 講義資料, 講義中に使用する C 言語プログラムと初期値データ, ヘリカル波のアニメーションをウェブで公開しています :
非線形数理秋の学校 パターン形成の数理とその周辺 - 反応拡散方程式理論による時 空間パターンの解析を中心に - 2007 年 9 月 25 日 -27 日 モデル方程式を通してみるパターン解析ー進行波からヘリカル波の分岐を例としてー 池田勉 ( 龍谷大学理工学部 ) 講義概要, 講義資料, 講義中に使用する C 言語プログラムと初期値データ, ヘリカル波のアニメーションをウェブで公開しています :
代数 幾何 < ベクトル > 1 ベクトルの演算 和 差 実数倍については 文字の計算と同様 2 ベクトルの成分表示 平面ベクトル : a x e y e x, ) ( 1 y1 空間ベクトル : a x e y e z e x, y, ) ( 1 1 z1
 代数 幾何 < ベクトル > ベクトルの演算 和 差 実数倍については 文字の計算と同様 ベクトルの成分表示 平面ベクトル :, 空間ベクトル : z,, z 成分での計算ができるようにすること ベクトルの内積 : os 平面ベクトル :,, 空間ベクトル :,,,, z z zz 4 ベクトルの大きさ 平面上 : 空間上 : z は 良く用いられる 5 m: に分ける点 : m m 図形への応用
代数 幾何 < ベクトル > ベクトルの演算 和 差 実数倍については 文字の計算と同様 ベクトルの成分表示 平面ベクトル :, 空間ベクトル : z,, z 成分での計算ができるようにすること ベクトルの内積 : os 平面ベクトル :,, 空間ベクトル :,,,, z z zz 4 ベクトルの大きさ 平面上 : 空間上 : z は 良く用いられる 5 m: に分ける点 : m m 図形への応用
Microsoft Word - 非線形計画法 原稿
 非線形計画法条件付き最適化問題は目的関数と制約条件で示すが この中に一つでも 次式でないものが含まれる問題を総称して非線形計画法いう 非線形計画問題は 多くの分野で研究されているが 複雑性により十分汎用的なものは確立されておらず 限定的なものに限り幾つかの提案がなされている ここでは簡単な解法について紹介する. 制約なし極値問題 単純問題の解法 変数で表される関数 の極値は を解くことによって求められる
非線形計画法条件付き最適化問題は目的関数と制約条件で示すが この中に一つでも 次式でないものが含まれる問題を総称して非線形計画法いう 非線形計画問題は 多くの分野で研究されているが 複雑性により十分汎用的なものは確立されておらず 限定的なものに限り幾つかの提案がなされている ここでは簡単な解法について紹介する. 制約なし極値問題 単純問題の解法 変数で表される関数 の極値は を解くことによって求められる
ディジタル信号処理
 ディジタルフィルタの設計法. 逆フィルター. 直線位相 FIR フィルタの設計. 窓関数法による FIR フィルタの設計.5 時間領域での FIR フィルタの設計 3. アナログフィルタを基にしたディジタル IIR フィルタの設計法 I 4. アナログフィルタを基にしたディジタル IIR フィルタの設計法 II 5. 双 次フィルタ LI 離散時間システムの基礎式の証明 [ ] 4. ] [ ]*
ディジタルフィルタの設計法. 逆フィルター. 直線位相 FIR フィルタの設計. 窓関数法による FIR フィルタの設計.5 時間領域での FIR フィルタの設計 3. アナログフィルタを基にしたディジタル IIR フィルタの設計法 I 4. アナログフィルタを基にしたディジタル IIR フィルタの設計法 II 5. 双 次フィルタ LI 離散時間システムの基礎式の証明 [ ] 4. ] [ ]*
3 数値解の特性 3.1 CFL 条件 を 前の章では 波動方程式 f x= x0 = f x= x0 t f c x f =0 [1] c f 0 x= x 0 x 0 f x= x0 x 2 x 2 t [2] のように差分化して数値解を求めた ここでは このようにして得られた数値解の性質を 考
![3 数値解の特性 3.1 CFL 条件 を 前の章では 波動方程式 f x= x0 = f x= x0 t f c x f =0 [1] c f 0 x= x 0 x 0 f x= x0 x 2 x 2 t [2] のように差分化して数値解を求めた ここでは このようにして得られた数値解の性質を 考 3 数値解の特性 3.1 CFL 条件 を 前の章では 波動方程式 f x= x0 = f x= x0 t f c x f =0 [1] c f 0 x= x 0 x 0 f x= x0 x 2 x 2 t [2] のように差分化して数値解を求めた ここでは このようにして得られた数値解の性質を 考](/thumbs/103/158269281.jpg) 3 数値解の特性 3.1 CFL 条件 を 前の章では 波動方程式 f x= x = f x= x t f c x f = [1] c f x= x f x= x 2 2 t [2] のように差分化して数値解を求めた ここでは このようにして得られた数値解の性質を 考える まず 初期時刻 t=t に f =R f exp [ik x ] [3] のような波動を与えたとき どのように時間変化するか調べる
3 数値解の特性 3.1 CFL 条件 を 前の章では 波動方程式 f x= x = f x= x t f c x f = [1] c f x= x f x= x 2 2 t [2] のように差分化して数値解を求めた ここでは このようにして得られた数値解の性質を 考える まず 初期時刻 t=t に f =R f exp [ik x ] [3] のような波動を与えたとき どのように時間変化するか調べる
DVIOUT
 第 3 章 フーリエ変換 3.1 フーリエ積分とフーリエ変換 第 章では 周期を持つ関数のフーリエ級数について学びました この章では 最初に 周期を持つ関数のフーリエ級数を拡張し 周期を持たない ( 一般的な ) 関数のフーリエ級数を導きましょう 具体的には 関数 f(x) を区間 L x L で考え この L を限りなく大きくするというアプローチを取ります (L ) なお ここで扱う関数 f(x)
第 3 章 フーリエ変換 3.1 フーリエ積分とフーリエ変換 第 章では 周期を持つ関数のフーリエ級数について学びました この章では 最初に 周期を持つ関数のフーリエ級数を拡張し 周期を持たない ( 一般的な ) 関数のフーリエ級数を導きましょう 具体的には 関数 f(x) を区間 L x L で考え この L を限りなく大きくするというアプローチを取ります (L ) なお ここで扱う関数 f(x)
2 Hermite-Gaussian モード 2-1 Hermite-Gaussian モード 自由空間を伝搬するレーザ光は次のような Hermite-gaussian Modes を持つ光波として扱う ことができる ここで U lm (x, y, z) U l (x, z)u m (y, z) e
 Wavefront Sensor 法による三角共振器のミスアラインメント検出 齊藤高大 新潟大学大学院自然科学研究科電気情報工学専攻博士後期課程 2 年 214 年 8 月 6 日 1 はじめに Input Mode Cleaner(IMC) は Fig.1 に示すような三角共振器である 懸架鏡の共振などにより IMC を構成する各ミラーが角度変化を起こすと 入射光軸と共振器軸との間にずれが生じる
Wavefront Sensor 法による三角共振器のミスアラインメント検出 齊藤高大 新潟大学大学院自然科学研究科電気情報工学専攻博士後期課程 2 年 214 年 8 月 6 日 1 はじめに Input Mode Cleaner(IMC) は Fig.1 に示すような三角共振器である 懸架鏡の共振などにより IMC を構成する各ミラーが角度変化を起こすと 入射光軸と共振器軸との間にずれが生じる
Microsoft PowerPoint - DigitalMedia2_3b.pptx
 Contents デジタルメディア処理 2 の概要 フーリエ級数展開と 離散とその性質 周波数フィルタリング 担当 : 井尻敬 とは ( ) FourierSound.py とは ( ) FourierSound.py 横軸が時間の関数を 横軸が周波数の関数に変換する 法 声周波数 周波数 ( 係数番号 ) 後の関数は元信号に含まれる正弦波の量を す 中央に近いほど低周波, 外ほどが 周波 中央 (
Contents デジタルメディア処理 2 の概要 フーリエ級数展開と 離散とその性質 周波数フィルタリング 担当 : 井尻敬 とは ( ) FourierSound.py とは ( ) FourierSound.py 横軸が時間の関数を 横軸が周波数の関数に変換する 法 声周波数 周波数 ( 係数番号 ) 後の関数は元信号に含まれる正弦波の量を す 中央に近いほど低周波, 外ほどが 周波 中央 (
5-仮想仕事式と種々の応力.ppt
 1 以上, 運動の変数についての話を終える. 次は再び力の変数に戻る. その前に, まず次の話が唐突と思われないように 以下は前置き. 先に, 力の変数と運動の変数には対応関係があって, 適当な内積演算によって仕事量を表す ことを述べた. 実は,Cauchy 応力と速度勾配テンソル ( あるいは変位勾配テンソル ) を用いると, それらの内積は内部仮想仕事を表していて, そして, それは外力がなす仮想仕事に等しいという
1 以上, 運動の変数についての話を終える. 次は再び力の変数に戻る. その前に, まず次の話が唐突と思われないように 以下は前置き. 先に, 力の変数と運動の変数には対応関係があって, 適当な内積演算によって仕事量を表す ことを述べた. 実は,Cauchy 応力と速度勾配テンソル ( あるいは変位勾配テンソル ) を用いると, それらの内積は内部仮想仕事を表していて, そして, それは外力がなす仮想仕事に等しいという
Taro-F25理論 印刷原稿
 第 種理論 A 問題 ( 配点は 問題当たり小問各 点, 計 0 点 ) 問 次の文章は, 真空中の静電界に関する諸法則の微分形に関する記述である 文中の に当てはまるものを解答群の中から選びなさい 図のように, 直交座標系において電界の z 軸成分が零となるような電界について, y 平面の二次元で電位や電界を考える ここで,4 点 (h,0),(0,h), (- h,0),(0,-h) の電位がそれぞれ
第 種理論 A 問題 ( 配点は 問題当たり小問各 点, 計 0 点 ) 問 次の文章は, 真空中の静電界に関する諸法則の微分形に関する記述である 文中の に当てはまるものを解答群の中から選びなさい 図のように, 直交座標系において電界の z 軸成分が零となるような電界について, y 平面の二次元で電位や電界を考える ここで,4 点 (h,0),(0,h), (- h,0),(0,-h) の電位がそれぞれ
2011年度 筑波大・理系数学
 0 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ O を原点とするy 平面において, 直線 y= の を満たす部分をC とする () C 上に点 A( t, ) をとるとき, 線分 OA の垂直二等分線の方程式を求めよ () 点 A が C 全体を動くとき, 線分 OA の垂直二等分線が通過する範囲を求め, それ を図示せよ -- 0 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ
0 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ O を原点とするy 平面において, 直線 y= の を満たす部分をC とする () C 上に点 A( t, ) をとるとき, 線分 OA の垂直二等分線の方程式を求めよ () 点 A が C 全体を動くとき, 線分 OA の垂直二等分線が通過する範囲を求め, それ を図示せよ -- 0 筑波大学 ( 理系 ) 前期日程問題 解答解説のページへ
<4D F736F F D20824F E B82CC90FC90CF95AA2E646F63>
 1/1 平成 3 年 6 月 11 日午前 1 時 3 分 4 ベクトルの線積分 4 ベクトルの線積分 Ⅰ. 積分の種類 通常の物理で使う積分には 3 種類あります 積分変数の数に応じて 線積分 ( 記号 横(1 重 d, dy, dz d ( ine: 面積分 ( 記号 縦 横 ( 重 線 4 ベクトルの線積分 重積分記号 ddy, dydz, dzdz ds ( Surface: 1 重積分記号
1/1 平成 3 年 6 月 11 日午前 1 時 3 分 4 ベクトルの線積分 4 ベクトルの線積分 Ⅰ. 積分の種類 通常の物理で使う積分には 3 種類あります 積分変数の数に応じて 線積分 ( 記号 横(1 重 d, dy, dz d ( ine: 面積分 ( 記号 縦 横 ( 重 線 4 ベクトルの線積分 重積分記号 ddy, dydz, dzdz ds ( Surface: 1 重積分記号
Microsoft PowerPoint - qcomp.ppt [互換モード]
![Microsoft PowerPoint - qcomp.ppt [互換モード] Microsoft PowerPoint - qcomp.ppt [互換モード]](/thumbs/85/91243661.jpg) 量子計算基礎 東京工業大学 河内亮周 概要 計算って何? 数理科学的に 計算 を扱うには 量子力学を計算に使おう! 量子情報とは? 量子情報に対する演算 = 量子計算 一般的な量子回路の構成方法 計算って何? 計算とは? 計算 = 入力情報から出力情報への変換 入力 計算機構 ( デジタルコンピュータ,etc ) 出力 計算とは? 計算 = 入力情報から出力情報への変換 この関数はどれくらい計算が大変か??
量子計算基礎 東京工業大学 河内亮周 概要 計算って何? 数理科学的に 計算 を扱うには 量子力学を計算に使おう! 量子情報とは? 量子情報に対する演算 = 量子計算 一般的な量子回路の構成方法 計算って何? 計算とは? 計算 = 入力情報から出力情報への変換 入力 計算機構 ( デジタルコンピュータ,etc ) 出力 計算とは? 計算 = 入力情報から出力情報への変換 この関数はどれくらい計算が大変か??
静的弾性問題の有限要素法解析アルゴリズム
 概要 基礎理論. 応力とひずみおよび平衡方程式. 降伏条件式. 構成式 ( 応力 - ひずみ関係式 ) 有限要素法. 有限要素法の概要. 仮想仕事の原理式と変分原理. 平面ひずみ弾性有限要素法定式化 FEM の基礎方程式平衡方程式. G G G ひずみ - 変位関係式 w w w. kl jkl j D 構成式応力 - ひずみ関係式 ) (. 変位の境界条件力の境界条件境界条件式 t S on V
概要 基礎理論. 応力とひずみおよび平衡方程式. 降伏条件式. 構成式 ( 応力 - ひずみ関係式 ) 有限要素法. 有限要素法の概要. 仮想仕事の原理式と変分原理. 平面ひずみ弾性有限要素法定式化 FEM の基礎方程式平衡方程式. G G G ひずみ - 変位関係式 w w w. kl jkl j D 構成式応力 - ひずみ関係式 ) (. 変位の境界条件力の境界条件境界条件式 t S on V
<4D F736F F D FCD B90DB93AE96402E646F63>
 7 章摂動法講義のメモ 式が複雑なので 黒板を何度も修正したし 間違ったことも書いたので メモを置きます 摂動論の式の導出無摂動系 先ず 厳密に解けている Schrödiger 方程式を考える,,,3,... 3,,,3,... は状態を区別する整数であり 状態 はエネルギー順に並んでいる 即ち は基底状態 は励起状態である { m } は相互に規格直交条件が成立する k m k mdx km k
7 章摂動法講義のメモ 式が複雑なので 黒板を何度も修正したし 間違ったことも書いたので メモを置きます 摂動論の式の導出無摂動系 先ず 厳密に解けている Schrödiger 方程式を考える,,,3,... 3,,,3,... は状態を区別する整数であり 状態 はエネルギー順に並んでいる 即ち は基底状態 は励起状態である { m } は相互に規格直交条件が成立する k m k mdx km k
