ハートリー・フォック(HF)法とは?
|
|
|
- なつき ひろき
- 4 years ago
- Views:
Transcription
1 大学院講義 電子相関編 阿部穣里
2 目的 電子相関法はハートリー フォック (F) 法に対してより良い電子状態の記述を行う理論です 主に量子化学で用いられるのが 配置換相互作用 (CI) 法多体摂動論 (PT) 法クラスター展開 (CC) 法です 電子相関法に慣れるために 最小基底を用いた 分子の Full CI 法と MP 法について 自ら導出を行い エクセルでポテンシャル曲線を求めます
3 アウトライン (CI 法 ) F の波動関数とは? その満たすべき条件 分子のハミルトニアン エネルギー期待値を計算しよう 他の配置のエネルギーを求めよう 配置間の行列要素を計算しよう スピンの固有状態を考えよう CI とは? ラグランジュの未定乗数法 エクセルで計算してみよう
4 アウトライン (MP 法 ) 次摂動論の一般式を求めよう ゼロ次のハミルトニアン その固有値は? MP 法の表式を求めよう エクセルでMPのエネルギーを求めよう F,CI,MPのポテンシャルの比較を行おう
5 ハートリー フォック (F) 法とは? Lnear Combnaton of Atom Orbtal (LCAO) 近似を 用いてより良い 電子軌道 ( 分子軌道 ) を作る方法 φ ( r) χ ( r) p p p 分子軌道 (MO) 係数 ( 求めたいもの ) 基底関数 ( 原子軌道を参考に作られる既知関数 )
6 反対称性原理 つの電子の座標の交換に対して 交換 電子 電子 電子 電子 波動関数の符号が変わる フェルミ粒子の性質 ( τ, τ ) ( τ, τ ) τ ( x, y, z, ω ) 電子 の位置座標 電子 のスピン座標
7 スレーター行列式 準位系のスレーター行列式 行列式を取る ( τ, τ ) ψ ψ ( τ ) ψ ( τ ) ( τ ) ψ ( τ ) ψ ψ ψ ψ ( ( τ ) ( τ ) ( τ ) ( τ ))
8 スレーター行列式 前の式の つの電子の座標を入れかれると τ, τ ψ τ ψ τ ψ τ ψ τ τ τ, 行列式で表現すると反対称性原理を満たす! 行列式は 行や列の入れ替えで負の符号を与える
9 スレーター行列式 つの電子が全く同じ座標にいる場合 ( τ, τ ) ( τ ) ( τ ) ( τ ) ( τ ) ψ ψ ψ ψ つの電子が同じ位置で同じスピンになる確率は Paul の排他原理も表現できている 行列式は 同じ値の行や列があると になる
10 スレーター行列式 準位系のスレーター行列式 ( τ, τ ) ψ ψ ( τ ) ψ ( τ ) ( τ ) ψ ( τ ) τ τ ψ ψ 場所をとり面倒なので スレーター行列式を上のように記述することにする
11 スピン軌道と空間軌道 番目の空間軌道 φ ( r) χ ( r) p p p スピン軌道 ( r) ψ φ α ω τ または ψ τ φ r β ω 上スピンのスピン関数 下スピンのスピン関数
12 空間軌道 規格直交性 * * d j j r r r φ φ δ スピン関数 F 法で得られる空間軌道 ( 正準軌道 ) は規格直交性を満たす α * ω β ω * dω β ω α ω dω α * ω α ω * dω β ω β ω dω これはこういうものとして受け入れる α,β の形は問わない
13 Q. 以下のスレーター行列式を書き下せ つの空間軌道に 電子が占有している (STO-G 基底を使った 分子 ) φ φ 重項で最安定な詰まり方は ψ φ α ω ( τ) ( r ) ψ τ φ r β ω τ τ F ψ ψ r r φ α ω φ β ω
14 F Q. さらに書き下すと ( φ ( r ) α( ω ) φ ( r ) β( ω ) φ ( r ) α( ω ) φ ( r ) β( ω )) この波動関数に対して 全エネルギーを求めていくことにする F F e F
15 電子ハミルトニアン 分子のハミルトニアン total A e A M A 核の運動エネルギー演算子 ( 電子状態への影響が小さく無視 ) e 電子の運エネ電子 - 核引力電子 - 電子反発核 - 核反発 Z A A r R A > j j A> B A r r R R B hˆ hˆ r, j, j > j > j gˆ r r gˆ V ( R) 電子演算子 電子演算子 定数扱い ( 電子座標なし )
16 F F e F 分子のエネルギー hˆ gˆ V hˆ hˆ hˆ R F F F, j F > j ( 電子 核 ) 系の時 A ˆ ZA ZB h ( r) r R r R A ここは電子波動関数に変化を与えないいわば定数なので 最後に足せばいい F ˆ ZA ZB h ( r) r R r R B B V ( R) F ˆ ˆ g, j g,, > j ĝ r r
17 エネルギーの計算 h ˆ r h ˆ r g ˆ F F F F F, F に ( r ) ( r ) ( r ) ( r ) F φ α ω φ β ω φ α ω φ β ω を代入して 積分計算を実行する
18 エネルギーの計算 ( ) dr dr dω dω φ r α ω φ r β ω φ r α ω φ r β ω hˆ ( r ) hˆ ( r ) r r ( φ( r) α( ω) φ( r) β( ω) φ( r) α( ω) φ( r) β( ω) ) * 展開すると 個の 項存在する!( 面倒 ) 積分変数ごとに計算を分けることができる 特にスピン座標の積分は中の演算子に依存しないことを利用する
19 規格化条件より 例 ( ) dr dr dω dω φ r α ω φ r β ω φ r α ω φ r β ω エネルギーの計算 hˆ ( r ) hˆ ( r ) ここだけ何か値あり r r ( φ( r) α( ω) φ( r) β( ω) φ( r) α( ω) φ( r) β( ω) ) ˆ φ h φ r h r r dr * φ ( r ) hˆ ( r ) φ ( r ) dr φ ( r ) φ ( r ) dr * * α ω α ω dω β ω β ω dω h * * と置く *
20 規格化条件より 例 ( ) dr dr dω dω φ r α ω φ r β ω φ r α ω φ r β ω エネルギーの計算 hˆ ( r ) hˆ ( r ) r r ( φ( r) α( ω) φ( r) β( ω) φ( r) α( ω) φ( r) β( ω) ) ここだけ何か値あり φ ( r ) φ ( r ) dr φ ( r ) hˆ ( r ) φ ( r ) dr * * α ω α ω dω β ω β ω dω h * * *
21 例 ( ) dr dr dω dω φ r α ω φ r β ω φ r α ω φ r β ω エネルギーの計算 hˆ ( r ) hˆ ( r ) r r ( φ( r) α( ω) φ( r) β( ω) φ( r) α( ω) φ( r) β( ω) ) ここだけ何か値あり ( ) と定義 φ ( r ) φ ( r ) φ ( r ) φ ( r ) drdr * * r r d d ( ) α ω α ω ω β ω β ω ω * * 規格化条件より *
22 例 4 ( ) dr dr dω dω φ r α ω φ r β ω φ r α ω φ r β ω エネルギーの計算 hˆ ( r ) hˆ ( r ) r r ( φ( r) α( ω) φ( r) β( ω) φ( r) α( ω) φ( r) β( ω) ) * ˆ ˆ φ r φ r h r h( r ) φ ( r ) φ ( r ) drdr * * r r d α ω β ω ω β ω α ω dω * * 直交条件より
23 電子 ( 分子軌道 ) 積分 ( j kl ) 積分の略称の定義 * ˆ j j h φ h φ d r r r r 電子 ( 分子軌道 ) 積分 ( 化学者の記法 ) 複素共役を取る軌道 電子座標 電子座標 φ r φ r φ r φ r * * j k l r r drdr 電子相関のエネルギーは, 電子分子軌道積分を用いて表現される
24
25 課題. F のエネルギー ( 核ポテンシャル項を除く ) を, 電子積分の記法を用いて表せ. 以下の配置に対応する波動関数を書き下し そのエネルギーも と同様に表せ φ φ φ φ φ φ 4
26
27 課題. V( R) j e j としたときに を求めよ,, 4,, 4, 4 φ φ φ φ φ φ φ φ ( ) F 4
28
29 スピン演算子 ˆ S S ˆz SS S z ( 非相対論の ) 波動関数は S 演算子と S z 演算子の固有状態でなければならない S: スピン S: スピン多重度 ( 重項 重項 ) S z : スピンのz 成分合成スピン演算子は 電子スピン演算子の和で 記述できる Sˆ SS ˆ ˆ SS ˆ ˆ Sˆ z Sˆ ˆ s ω S s ( ω ) ˆ ˆ Sˆ sˆ ω z z
30 電子スピン演算子 電子スピン演算子は以下の性質を満たす sˆ x ( ωαω ) βω sˆ x ( ω) β( ω) α( ω) sˆ y ( ωαω ) βω sˆ y ( ω) β( ω) α( ω) sˆ z ( ω) α( ω) α( ω) sˆ z ( ω) β( ω) β( ω) さらに以下の昇降演算子を定義すると計算が楽 上昇演算子 ( ω) ( ω) ( ω) sˆ ˆ ˆ sx s 下降演算子 ( ω) ( ω) ( ω) sˆ ˆ ˆ sx s スピンを 増やす y y スピンを 減らす ( ωαω ) ŝ ( ω) β( ω) α( ω) sˆ ŝ ( ωαω ) βω ( ω) β( ω) sˆ
31 課題. 課題. で書き下した波動関数について,, 4, 4 スピン部分だけをまとめよ を書き出し
32 課題. 先の問題で得られたスピン関数に対して Ŝ と S を作用させた計算を行え ˆz α( ω) β( ω) α( ω) β( ω) と α( ω) β( ω) α( ω) β( ω) Sˆ SS ˆ ˆ ˆ ˆ ˆ SS S z を作用するために必要な計算を以下に行う Sˆ sˆ sˆ α( ω) β( ω) ( ω) ( ω) α ω β ω α ω α ω Ŝ β( ω) α( ω) α( ω) α( ω) を考えればよい α( ω) β( ω) ( ω) ( ω) α ω β ω β ω β ω Ŝ β( ω) α( ω) β( ω) β( ω) Sˆ sˆ sˆ Ŝ α ω α ω α ω β ω β ω α ω Ŝ β ω β ω α ω β ω β ω α ω ˆ S ( ˆ ˆ z α ω β ω sz ω sz( ω) ) α( ω) β( ω) α( ω) β( ω) α( ω) β( ω) Sˆ z β ω α ω Sˆz は α ω β ω α ω β ω, α ω β ω α ω β ω どちらも Ŝ は ( SS SS ) Sz α( ω) β( ω) α( ω) β( ω) ˆ ˆ ˆ ˆ ˆ 固有値はS(S), ( SS ˆ ˆ SS ˆ ˆ ) S ˆ S z α( ω) β( ω) α( ω) β( ω) α( ω) β( ω) α( ω) β( ω) 固有値は S(S) S( 重項 )
33 準位 電子系の取りうる電子配置 ( スレーター行列式は 6 つ!) φ φ [ φ ( r ) α( ω ) φ ( r ) β ( ω ) φ ( r ) α( ω ) φ ( r ) β ( ω )] [ φ ( r ) α( ω ) φ ( r ) β ( ω ) φ ( r ) α( ω ) φ ( r ) β ( ω )] そのままで正しい 重項 (S z ) ( つまりスピン演算子の固有状態 ) ˆ S S S, S, S > 重項 そのままで正しい 重項 (S z ) [ φ ( r ) α( ω ) φ ( r ) β ( ω ) φ ( r ) α( ω ) φ ( r ) β ( ω )] ( ) 4 が正しい 重項 (S z ) 4 φ( r) β( ω) φ( r) α( ω) φ( r) β( ω) φ( r) α( ω) ( 4 ) が正しい 重項 (S z ) 5 ϕ( r) α( ω) ϕ( r) α( ω) ϕ( r) α( ω) ϕ( r) α( ω) そのままで正しい 重項 (S z ) 6 ϕ( r) β( ω) ϕ( r) β( ω) ϕ( r) β( ω) ϕ( r) β( ω) そのままで正しい 重項 (S z -)
34
35 配置換相互作用 Confguraton nteraton (CI) CI... (F 配置 ) 異なる配置 F 配置 ( スレーター行列式 ) に別の配置のスレーター行列式の状態の線形結合をとると波動関数により自由度をもたせて記述できる ある基底関数を用いてすべての電子配置の線形結合をとる 完全 CI (FCI, Full CI) 完全系を成す基底関数の場合 FCI は厳密解に一致する電子相関は異なる配置をどう混ぜるかという問題
36 重項に限定すると配置は つ [ ] ω β φ ω α φ ω β φ ω α φ r r r r [ ] ω β φ ω α φ ω β φ ω α φ r r r r [ ] ω β φ ω α φ ω β φ ω α φ r r r r そのままで正しい 重項 (S z ) ( つまりスピン演算子の固有状態 ) そのままで正しい 重項 (S z ) 重項,, ˆ > S S S S S が正しい 重項 (S z ) 4 φ φ φ φ φ φ φ φ 4 ~ ~ FCI 重項として,, を最適化することでより良い波動関数を求める 4 r r r r φ β ω φ α ω φ β ω φ α ω
37 変分原理 C などの係数の決め方 厳密な固有状態の波動関数の エネルギーは ニセの波動関数よりも低い 偽 のエネルギー 偽 エネルギーが一致したら それは本物 Ĥ 偽 偽 偽 Ĥ 偽 偽
38 C などの係数の決め方 変分法 偽 偽 ニセの波動関数のエネルギーを より低くなるようにすれば 厳密解に近づく 偽 偽 偽 Ĥ 偽 偽 最小化の必要条件 を最小化する を選ぶ 偽 以降 偽の文字は省略
39 ラグランジュの未定乗数法 ~ ~ ~ ˆ ~ ˆ L FCI FCI FCI FCI ε ε ε * ε L をの制限のもとに 最小化したいとき上記の L を微分して調べればよい (ε はラグランジュの未定乗数係数 ) FCI FCI ˆ FCI FCI 他の微分の条件も加えると, などの行列要素の計算が必要 ( 課題 で行った!) ε ε ε
40 FCI 計算に必要な行列要素 IJ h ˆ ˆ h [ φ ( r ) α( ω ) φ ( r ) β ( ω ) φ ( r ) α( ω ) φ ( r ) β ( ω )] ϕ ( r ) α( ω ) ϕ ( r ) β( ω ) ϕ ( r ) α( ω ) ϕ ( r ) β( ω ) ( r ) hˆ ( r ) [ φ ( r ) α( ω ) φ ( r ) β ( ω ) φ ( r ) α( ω ) φ ( r ) β ( ω )] r dτ ˆ 4 ˆ ˆ h r h( r) r ϕ( r) β( ω) ϕ( r) α( ω) ϕ( r) β( ω) ϕ( r) α( ω) dτ h ( ) ブリルアンの定理より ˆ ˆ ˆ h 4 ˆ h ˆ h ( ) ( ) ˆ ~ ~ ˆ 値はあるが省略
41 ラグランジュの未定乗数法 ~ ~ ~ ˆ ~ ˆ L FCI FCI FCI FCI ε ε ε * ε L をの制限のもとに 最小化したいとき上記の L を微分して調べればよい (ε はラグランジュの未定乗数係数 ) FCI FCI ˆ FCI FCI 他の微分の条件も加えると 先の計算でここはゼロだったことに注意 ε ε ε
42 ε ε ε が自明な解以外を持つためには ε ε ε ε ε det ε ε ε ε こっちには今興味がないとしか混ざらない その逆行列が存在せず 行列式が つまり
43 課題.FCI エネルギー計算のステップ ( 準備 ) ( ) FCI 重項 に対して ε det ε つ解があることに注意 ( ε )( ε ) より ε を数式で求める それぞれの ε の時の, を数式で求める ただし ( 規格化条件 ) を満たすようにする 求めた, で ˆ FCI FCI を計算する式を作っておく
44 課題.FCI エネルギー計算のステップ ( エクセル ) 式ができたら エクセルにある hj, (j kl) の値を用いて,,, ε を求める また ( つある ) も求める それぞれの ε の時の, をエクセルで求める 対応するエネルギー ˆ FCI FCI もエクセルで求める そして 核エネルギーを足し 核間距離を横軸にしてプロットする
45 摂動論とは 変分法 (CI 法 ) とは異なる近似解を得る方法 ˆ ˆ ( ) ( ) これの解が知りたいけどわからないとき でもこっちの解 ( ) は完全にわかっている Ĥ と Ĥ が割と近いときに使える理論が摂動論 { ( ) } k をで展開して表現するが 展開係数は反復計算なしで求まる
46 摂動論 ˆ ˆ λv とする λ は任意の値をとるパラメータ ( ) λ λ 次エネルギー 次波動関数 次エネルギー 次波動関数 次エネルギー 次波動関数 ( ) λ λ ほんとは λ しか興味ないがトリックを使いたいのでこうする と呼ぶ ハミルトニアンが少し変化したのだから エネルギーも波動関数も変化する しかも λ の値に依存して変化しないとおかしい λ に対してテーラー展開で表現しておこう
47 摂動論 ˆ に全部代入 ( ( ) ˆ ) λv λ λ ( ( ) ) ( ) λ λ λ λ ( ) 見方を変えると この式は λ を変数とした多項式である λ にどんな値を代入しても この式は成立しないといけない λ の各次数の係数がすべて にならないといけない
48 摂動論 ( ( ) ˆ ) λv λ λ ( ( ) ) ( ) λ λ λ λ ( ) λ の 次の項 λ の 次の項 λ の 次の項 ( ( ) ( ) ( ) ) ˆ λ ˆ ( ( ) ( ) ( ) ) V ( ( ) V ) ˆ λ
49 摂動論 ( 波動関数 ) { ( ) } k は 次ハミルトニアンの固有状態であり 規格直交の組が無限個あって完全系を張っているので 次 次 の波動関数は 次の解の線形結合で記述できる ( ) k k k ( ) k k k 話すとややこしいので省くが 同じ状態の解はここには含めない ( 次波動関数に含まれる )
50 摂動論 ( 次の項 ) λ の 次の項 より ( ( ) ( ) ( ) λ ˆ ) V ˆ V ( ) ( ) k k を代入すると k ˆ V k k 左から ( ) ( * ) k をかけて積分すると ˆ ( ) V k k k
51 摂動論 ( 次の項 ) ˆ ( ) V k k k ( ) ( ) ( ) ( ) ( ) δ ˆ k k k k k ( 規格直交条件 ) 次波動関数は 次ハミルトニアンの固有状態 を用いると V ( ) ( )
52 摂動論 ( 次の波動関数 ) λ の 次の項 より ( ( ) ( ) ( ) λ ˆ ) V ˆ V ( ) ( ) k k を代入すると k ˆ V k k ( ) 左から * j j k をかけて積分すると ˆ ( ) V j k j k k
53 摂動論 ( 次の波動関数 ) ˆ ( ) V j k j k k ( ) ( ) ( ) ( ) ( ) δ ˆ k k k k k ( 規格直交条件 ) 次波動関数は 次ハミルトニアンの固有状態 を用いると j ( ) ( ) j ( ) ( ) j V
54 摂動論 ( 次の項 ) λの 次の項 ˆ ( ) ( ) λ V より ( ) k k k V ˆ ( ), ( ) k k k ( ) k を代入すると V ˆ 左から k k k k k k ( * ) をかけて積分すると V ˆ ( ) k k k k k
55 k 摂動論 ( 次の項 ) V ˆ k k k k k ( ) ( ) ( ) ( ) ( ) δ ˆ k k k k k ( 規格直交条件 ) 次波動関数は 次ハミルトニアンの固有状態 を用いると V ( ) ( ) k k k
56 摂動論 ( 次の項 ) ( ) V k k k と j ( ) ( ) j ( ) ( ) j V より V V ( ) ( ) ( ) ( ) k k ( ) ( ) k k
57 摂動論 ( 次の項 ) V ˆ ˆ ( ) ( ) ( ) ( ) k k ˆ ( ) ( ) ( ) ( ) ( ) k k k ˆ ( ) ( ) k ˆ ˆ ( ) ( ) ( ) ( ) k k ( ) ( ) k k 次の波動関数の解に対するハミルトニアン行列要素がわかれば 次摂動エネルギーは求めることができる
58 MP 法とフォック演算子 次のハミルトニアンをフォック演算子の和で定義 ˆ N e fˆ r ˆ fψ εψ F の分子軌道はフォック演算子の固有関数 電子項 電子項 フォック演算子 fˆ ( r) ˆ ( ˆ ˆ ) h r J j K j N e j クーロン演算子 交換演算子 J r d * ˆ j ψ ψ j τ ψ j τ ψ τ τ r K r d * ˆ j ψ ψ j τ ψ τ ψ j τ τ r
59 電子 軌道系のフォック演算子 空間軌道は 種類 スピン軌道は 4 種類ある φ ψ φ α( ω) τ r ψ ( τ) φ ( r) β( ω) 占有軌道 φ ( τ) ( r ) ψ ( τ) φ ( r) β( ω) ψ φ α ω 4 電子 軌道の 電子演算子 総和は占有軌道でとる クーロン演算子 交換演算子 j j J d d * * ˆ ψ τ ψ τ ψ τ j r ψ τ τ ψ τ ψ τ r ψ τ τ K d d * * ˆ ψ τ ψ τ ψ τ j r ψ τ τ ψ τ ψ τ r ψ τ τ
60 電子 軌道系のフォック演算子 課題 ε ψ fˆ ψ, ε ψ fˆ ψ を計算せよ フォック演算子の各項計算する, 電子積分の表記は前頁を参照 ψ Jˆ j j ( r ) ( r ) ( r ) ( r ) * * r φ α ω φ β ω φ β ω φ α ω dτ dτ ( r ) ( r ) ( r ) ( r ) * * r ψ * * ψ ( τ) ψ ( τ) ψ ( τ) ψ( τ) dτdτ r * * ψ ( τ) ψ( τ) ψ ( τ) ψ( τ) dτdτ r φ α ω φ α ω φ α ω φ α ω dτ dτ
61 電子 軌道系のフォック演算子 課題 ε ψ fˆ ψ, ε ψ fˆ ψ を計算せよ フォック演算子の各項計算する, 電子積分の表記は前頁を参照 ψ Kˆ j j ψ τ ψ τ ψ τ ψ τ dτ dτ ψ τ ψ τ ψ τ ψ τ dτ dτ * * * * r r φ α ω φ α ω φ α ω φ α ω dτ dτ ( r ) ( r ) ( r ) ( r ) * * r φ α ω φ β ω φ α ω φ β ω dτ dτ ( r ) ( r ) ( r ) ( r ) * * r ψ ε ψ f ˆ ψ h 対称性から ε でも同じ値
62 電子 軌道系のフォック演算子 課題 ε ψ fˆ ψ, ε ψ fˆ ψ を計算せよ ψ Jˆ j j ψ τ ψ τ ψ τ ψ τ dτ dτ ψ τ ψ τ ψ τ ψ τ dτ dτ フォック演算子の各項計算する, 電子積分の表記は前頁を参照 * * * * r r φ α ω φ α ω φ α ω φ α ω dτ dτ ( r ) ( r ) ( r ) ( r ) * * r φ α ω φ β ω φ β ω φ α ω dτ dτ ( r ) ( r ) ( r ) ( r ) * * r ψ
63 電子 軌道系のフォック演算子 課題 ε ψ fˆ ψ, ε ψ fˆ ψ を計算せよ ψ Kˆ j j ψ τ ψ τ ψ τ ψ τ dτ dτ ψ τ ψ τ ψ τ ψ τ dτ dτ フォック演算子の各項計算する, 電子積分の表記は前頁を参照 * * * * r r φ α ω φ α ω φ α ω φ α ω dτ dτ ( r ) ( r ) ( r ) ( r ) * * r φ α ω φ β ω φ α ω φ β ω dτ dτ ( r ) ( r ) ( r ) ( r ) * * r ψ ε ψ f ˆ ψ h 対称性から ε 4 でも同じ値
64 次エネルギー ˆ fˆ τ fˆ τ fˆ τ ˆ fψ εψ のとき ˆ ˆ を求めよ, φ φ [ φ ( r ) α( ω ) φ ( r ) β ( ω ) φ ( r ) α( ω ) φ ( r ) β ( ω )] φ φ [ φ ( r ) α( ω ) φ ( r ) β ( ω ) φ ( r ) α( ω ) φ ( r ) β ( ω )] ( ) F
65
66 次エネルギー ( fˆ ( τ) fˆ ( τ) ) ( fˆ ( τ) fˆ ( τ) ) ψ( τ) ψ( τ) ψ( τ) ψ( τ) ( ε ε) ψ( τ) ψ( τ) ψ( τ) ψ( τ) ( ε ε) ( εψ ( τ) ψ( τ) εψ( τ) ψ( τ) ) εψ( τ) ψ( τ) εψ ( τ) ψ( τ) ( fˆ ( τ) fˆ ( τ) ) ( fˆ ( τ) fˆ ( τ) ) ψ( τ) ψ4( τ) ψ( τ) ψ4( τ) ( ε ε ) 4, どちらも Ĥ の固有状態になる 一般に F の 電子軌道で得られるスレーター行列式は Ĥ の固有状態
67 MP エネルギーを求めよう,, 次のエネルギーの和を求める必要がある の基底状態を考えると 次関数は F 関数に対応 次を示す添え字を省略し CI の時に表わした配置の関数の記法で表す ( ) ˆ V k ˆ ˆ k k k
68 次 次は MP エネルギーを求めよう ( ) ˆ V ˆ ˆ これは以前に求めた F エネルギーに等しい 次の項に含めるべき励起配置は? k ˆ ˆ k k k CI の時に計算した配置間の行列要素 重項 かつFとの行列要素がにならない のみ
69 MP エネルギーを求めよう ( ) ˆ ˆ ˆ 行列要素はすでに CI の時に計算済み φ φ ( ) F φ φ 分母の を, 電子積分で表わし MP エネルギー ( ) をエクセルで計算
70 最後の課題! エクセルで F, CI, MP のポテンシャルカーブを同一の図に記述しよう これまで計算した項に核ポテンシャルの項が含まれないので 最後に V R を足すことを忘れずに Gaussan で STO-G 基底を用いた 分子の計算を行い F,CI,MP のエネルギーが 自分が求めたものと一致するか確認せよ ( やり方は理論研の学生に聞く ) 核間距離については,, a.u. のみ行えばよい
Microsoft PowerPoint - H21生物計算化学2.ppt
 演算子の行列表現 > L いま 次元ベクトル空間の基底をケットと書くことにする この基底は完全系を成すとすると 空間内の任意のケットベクトルは > > > これより 一度基底を与えてしまえば 任意のベクトルはその基底についての成分で完全に記述することができる これらの成分を列行列の形に書くと M これをベクトル の基底 { >} による行列表現という ところで 行列 A の共役 dont 行列は A
演算子の行列表現 > L いま 次元ベクトル空間の基底をケットと書くことにする この基底は完全系を成すとすると 空間内の任意のケットベクトルは > > > これより 一度基底を与えてしまえば 任意のベクトルはその基底についての成分で完全に記述することができる これらの成分を列行列の形に書くと M これをベクトル の基底 { >} による行列表現という ところで 行列 A の共役 dont 行列は A
ハートレー近似(Hartree aproximation)
 ハートリー近似 ( 量子多体系の平均場近似 1) 0. ハミルトニアンの期待値の変分がシュレディンガー方程式と等価であること 1. 独立粒子近似という考え方. 電子系におけるハートリー近似 3.3 電子系におけるハートリー近似 Mde by R. Okmoto (Kyushu Institute of Technology) filenme=rtree080609.ppt (0) ハミルトニアンの期待値の変分と
ハートリー近似 ( 量子多体系の平均場近似 1) 0. ハミルトニアンの期待値の変分がシュレディンガー方程式と等価であること 1. 独立粒子近似という考え方. 電子系におけるハートリー近似 3.3 電子系におけるハートリー近似 Mde by R. Okmoto (Kyushu Institute of Technology) filenme=rtree080609.ppt (0) ハミルトニアンの期待値の変分と
Microsoft Word - 量子化学概論v1c.doc
 この講義ノートは以下の URL から入手できます http://www.sbchem.kyoto-u.ac.p/matsuda-lab/hase_fles/educaton_jh.html 量子化学概論講義ノート 3 正準 HF(Canoncal HF) 方程式 制限 HF(RHF) 方程式 HF-Roothaan(HFR) 方程式 京都大学工学研究科合成 生物化学専攻長谷川淳也 HF 解の任意性について式
この講義ノートは以下の URL から入手できます http://www.sbchem.kyoto-u.ac.p/matsuda-lab/hase_fles/educaton_jh.html 量子化学概論講義ノート 3 正準 HF(Canoncal HF) 方程式 制限 HF(RHF) 方程式 HF-Roothaan(HFR) 方程式 京都大学工学研究科合成 生物化学専攻長谷川淳也 HF 解の任意性について式
Microsoft Word - 8章(CI).doc
 8 章配置間相互作用法 : Configuration Interaction () etho [] 化学的精度化学反応の精密な解析をするためには エネルギー誤差は数 ~ kcal/mol 程度に抑えたいものである この程度の誤差内に治まる精度を 化学的精度 と呼ぶことがある He 原子のエネルギーをシュレーディンガー方程式と分子軌道法で計算した結果を示そう He 原子のエネルギー Hartree-Fock
8 章配置間相互作用法 : Configuration Interaction () etho [] 化学的精度化学反応の精密な解析をするためには エネルギー誤差は数 ~ kcal/mol 程度に抑えたいものである この程度の誤差内に治まる精度を 化学的精度 と呼ぶことがある He 原子のエネルギーをシュレーディンガー方程式と分子軌道法で計算した結果を示そう He 原子のエネルギー Hartree-Fock
Microsoft PowerPoint - 11JUN03
 基礎量子化学 年 4 月 ~8 月 6 月 3 日第 7 回 章分子構造 担当教員 : 福井大学大学院工学研究科生物応用化学専攻准教授前田史郎 -ail:saea@u-fukui.a.p URL:http://abio.abio.u-fukui.a.p/phyhe/aea/kougi 教科書 : アトキンス物理化学 ( 第 8 版 ) 東京化学同人 章原子構造と原子スペクトル 章分子構造 分子軌道法
基礎量子化学 年 4 月 ~8 月 6 月 3 日第 7 回 章分子構造 担当教員 : 福井大学大学院工学研究科生物応用化学専攻准教授前田史郎 -ail:saea@u-fukui.a.p URL:http://abio.abio.u-fukui.a.p/phyhe/aea/kougi 教科書 : アトキンス物理化学 ( 第 8 版 ) 東京化学同人 章原子構造と原子スペクトル 章分子構造 分子軌道法
<4D F736F F D FCD B90DB93AE96402E646F63>
 7 章摂動法講義のメモ 式が複雑なので 黒板を何度も修正したし 間違ったことも書いたので メモを置きます 摂動論の式の導出無摂動系 先ず 厳密に解けている Schrödiger 方程式を考える,,,3,... 3,,,3,... は状態を区別する整数であり 状態 はエネルギー順に並んでいる 即ち は基底状態 は励起状態である { m } は相互に規格直交条件が成立する k m k mdx km k
7 章摂動法講義のメモ 式が複雑なので 黒板を何度も修正したし 間違ったことも書いたので メモを置きます 摂動論の式の導出無摂動系 先ず 厳密に解けている Schrödiger 方程式を考える,,,3,... 3,,,3,... は状態を区別する整数であり 状態 はエネルギー順に並んでいる 即ち は基底状態 は励起状態である { m } は相互に規格直交条件が成立する k m k mdx km k
多次元レーザー分光で探る凝縮分子系の超高速動力学
 波動方程式と量子力学 谷村吉隆 京都大学理学研究科化学専攻 http:theochem.kuchem.kyoto-u.ac.jp TA: 岩元佑樹 iwamoto.y@kuchem.kyoto-u.ac.jp ベクトルと行列の作法 A 列ベクトル c = c c 行ベクトル A = [ c c c ] 転置ベクトル T A = [ c c c ] AA 内積 c AA = [ c c c ] c =
波動方程式と量子力学 谷村吉隆 京都大学理学研究科化学専攻 http:theochem.kuchem.kyoto-u.ac.jp TA: 岩元佑樹 iwamoto.y@kuchem.kyoto-u.ac.jp ベクトルと行列の作法 A 列ベクトル c = c c 行ベクトル A = [ c c c ] 転置ベクトル T A = [ c c c ] AA 内積 c AA = [ c c c ] c =
Microsoft Word - 5章摂動法.doc
 5 章摂動法 ( 次の Moller-Plesset (MP) 法のために ) // 水素原子など 電子系を除いては 原子系の Schrödiger 方程式を解析的に解くことはできない 分子系の Schrödiger 方程式の正確な数値解を求めることも困難である そこで Hartree-Fock(H-F) 法を導入した H-F 法は Schrödiger 方程式が与える全エネルギーの 99% を再現することができる優れた近似方法である
5 章摂動法 ( 次の Moller-Plesset (MP) 法のために ) // 水素原子など 電子系を除いては 原子系の Schrödiger 方程式を解析的に解くことはできない 分子系の Schrödiger 方程式の正確な数値解を求めることも困難である そこで Hartree-Fock(H-F) 法を導入した H-F 法は Schrödiger 方程式が与える全エネルギーの 99% を再現することができる優れた近似方法である
H AB φ A,1s (r r A )Hφ B,1s (r r B )dr (9) S AB φ A,1s (r r A )φ B,1s (r r B )dr (10) とした (S AA = S BB = 1). なお,H ij は共鳴積分 (resonance integra),s ij は重
 半経験量子計算法 : Tight-binding( 強結合近似 ) 計算の基礎 1. 基礎 Tight-binding 近似 ( 強結合近似, TB 近似あるいは TB 法などとも呼ばれる ) とは, 電子が強く拘束されており隣り合う軌道へ自由に移動できない, とする近似であり, 自由電子近似とは対極にある. 但し, 軌道間はわずかに重なり合っているので, 全く飛び移れないわけではない. Tight-binding
半経験量子計算法 : Tight-binding( 強結合近似 ) 計算の基礎 1. 基礎 Tight-binding 近似 ( 強結合近似, TB 近似あるいは TB 法などとも呼ばれる ) とは, 電子が強く拘束されており隣り合う軌道へ自由に移動できない, とする近似であり, 自由電子近似とは対極にある. 但し, 軌道間はわずかに重なり合っているので, 全く飛び移れないわけではない. Tight-binding
2012/10/17 第 3 章 Hückel 法 Schrödinger 方程式が提案された 1926 年から10 年を経た 1936 年に Hückel 法と呼ばれる分子軌道法が登場した 分子の化学的特徴を残しつつ 解法上で困難となる複雑な部分を最大限にカットした理論である Hückel 法は最
 //7 第 3 章 ükel 法 Shrödnger 方程式が提案された 96 年から 年を経た 936 年に ükel 法と呼ばれる分子軌道法が登場した 分子の化学的特徴を残しつつ 解法上で困難となる複雑な部分を最大限にカットした理論である ükel 法は最も単純な分子軌道法だが それによって生まれた考え方は化学者の概念となって現在に生き続けている ükel 近似の前提 ükel 近似の前提となっている主要な近似を列挙する
//7 第 3 章 ükel 法 Shrödnger 方程式が提案された 96 年から 年を経た 936 年に ükel 法と呼ばれる分子軌道法が登場した 分子の化学的特徴を残しつつ 解法上で困難となる複雑な部分を最大限にカットした理論である ükel 法は最も単純な分子軌道法だが それによって生まれた考え方は化学者の概念となって現在に生き続けている ükel 近似の前提 ükel 近似の前提となっている主要な近似を列挙する
Microsoft PowerPoint - 10.pptx
 m u. 固有値とその応用 8/7/( 水 ). 固有値とその応用 固有値と固有ベクトル 行列による写像から固有ベクトルへ m m 行列 によって線形写像 f : R R が表せることを見てきた ここでは 次元平面の行列による写像を調べる とし 写像 f : を考える R R まず 単位ベクトルの像 u y y f : R R u u, u この事から 線形写像の性質を用いると 次の格子上の点全ての写像先が求まる
m u. 固有値とその応用 8/7/( 水 ). 固有値とその応用 固有値と固有ベクトル 行列による写像から固有ベクトルへ m m 行列 によって線形写像 f : R R が表せることを見てきた ここでは 次元平面の行列による写像を調べる とし 写像 f : を考える R R まず 単位ベクトルの像 u y y f : R R u u, u この事から 線形写像の性質を用いると 次の格子上の点全ての写像先が求まる
1/30 平成 29 年 3 月 24 日 ( 金 ) 午前 11 時 25 分第三章フェルミ量子場 : スピノール場 ( 次元あり ) 第三章フェルミ量子場 : スピノール場 フェルミ型 ボーズ量子場のエネルギーは 第二章ボーズ量子場 : スカラー場 の (2.18) より ˆ dp 1 1 =
 / 平成 9 年 月 日 ( 金 午前 時 5 分第三章フェルミ量子場 : スピノール場 ( 次元あり 第三章フェルミ量子場 : スピノール場 フェルミ型 ボーズ量子場のエネルギーは 第二章ボーズ量子場 : スカラー場 の (.8 より ˆ ( ( ( q -, ( ( c ( H c c ë é ù û - Ü + c ( ( - に限る (. である 一方 フェルミ型は 成分をもち その成分を,,,,
/ 平成 9 年 月 日 ( 金 午前 時 5 分第三章フェルミ量子場 : スピノール場 ( 次元あり 第三章フェルミ量子場 : スピノール場 フェルミ型 ボーズ量子場のエネルギーは 第二章ボーズ量子場 : スカラー場 の (.8 より ˆ ( ( ( q -, ( ( c ( H c c ë é ù û - Ü + c ( ( - に限る (. である 一方 フェルミ型は 成分をもち その成分を,,,,
2018/6/12 表面の電子状態 表面に局在する電子状態 表面電子状態表面準位 1. ショックレー状態 ( 準位 ) 2. タム状態 ( 準位 ) 3. 鏡像状態 ( 準位 ) 4. 表面バンドのナローイング 5. 吸着子の状態密度 鏡像力によるポテンシャル 表面からzの位置の電子に働く力とポテン
 表面の電子状態 表面に局在する電子状態 表面電子状態表面準位. ショックレー状態 ( 準位. タム状態 ( 準位 3. 鏡像状態 ( 準位 4. 表面バンドのナローイング 5. 吸着子の状態密度 鏡像力によるポテンシャル 表面からzの位置の電子に働く力とポテンシャル e F z ( z z e V ( z ( Fz dz 4z e V ( z 4z ( z > ( z < のときの電子の運動を考える
表面の電子状態 表面に局在する電子状態 表面電子状態表面準位. ショックレー状態 ( 準位. タム状態 ( 準位 3. 鏡像状態 ( 準位 4. 表面バンドのナローイング 5. 吸着子の状態密度 鏡像力によるポテンシャル 表面からzの位置の電子に働く力とポテンシャル e F z ( z z e V ( z ( Fz dz 4z e V ( z 4z ( z > ( z < のときの電子の運動を考える
Microsoft PowerPoint - qchem3-9
 008 年度冬学期 量子化学 Ⅲ 章量子化学の応用 4.4. 相対論的効果 009 年 月 8 日 担当 : 常田貴夫准教授 相対性理論 A. Einstein 特殊相対論 (905 年 ) 相対性原理: ローレンツ変換に対して物理法則の形は不変 光速度不変 : 互いに等速運動する座標系で光速度は常に一定 ミンコフスキーの4 次元空間座標系 ( 等速系のみ ) 一般相対論 (96 年 ) 等価原理
008 年度冬学期 量子化学 Ⅲ 章量子化学の応用 4.4. 相対論的効果 009 年 月 8 日 担当 : 常田貴夫准教授 相対性理論 A. Einstein 特殊相対論 (905 年 ) 相対性原理: ローレンツ変換に対して物理法則の形は不変 光速度不変 : 互いに等速運動する座標系で光速度は常に一定 ミンコフスキーの4 次元空間座標系 ( 等速系のみ ) 一般相対論 (96 年 ) 等価原理
三重大学工学部
 反応理論化学 ( その 軌道相互作用 複数の原子が相互作用して分子が形成される複数の原子軌道 ( または混成軌道 が混合して分子軌道が形成される原子軌道 ( または混成軌道 が混合して分子軌道に変化すると軌道エネルギーも変化する. 原子軌道 原子軌道は3つの量子数 ( nlm,, の組合せにより指定される量子数の取り得る値の範囲 n の値が定まる l の範囲は n の値に依存して定まる m の範囲は
反応理論化学 ( その 軌道相互作用 複数の原子が相互作用して分子が形成される複数の原子軌道 ( または混成軌道 が混合して分子軌道が形成される原子軌道 ( または混成軌道 が混合して分子軌道に変化すると軌道エネルギーも変化する. 原子軌道 原子軌道は3つの量子数 ( nlm,, の組合せにより指定される量子数の取り得る値の範囲 n の値が定まる l の範囲は n の値に依存して定まる m の範囲は
三重大学工学部
 量子化学 : 量子力学を化学の問題に適用分子に対する Schödige 方程式を解く ˆ Ψ x, x, x,, x EΨ x, x, x,, x 3 N 3 Ĥ :milto 演算子 Ψ x, x, x,, x : 多電子波動関数, 3 N 反応理論化学 ( その ) E : エネルギー一般の多原子分子に対して厳密に解くことはできない N x : 電子の座標 ( 空間座標とスピン座標 ) Schödige
量子化学 : 量子力学を化学の問題に適用分子に対する Schödige 方程式を解く ˆ Ψ x, x, x,, x EΨ x, x, x,, x 3 N 3 Ĥ :milto 演算子 Ψ x, x, x,, x : 多電子波動関数, 3 N 反応理論化学 ( その ) E : エネルギー一般の多原子分子に対して厳密に解くことはできない N x : 電子の座標 ( 空間座標とスピン座標 ) Schödige
Microsoft Word - 9章(分子物性).doc
 1/1/6 9 章分子物性 1 節電気双極子モーメント (Electric Dipole Moment) 電子双極子モーメント とは 微小な距離 a だけ離れて点電荷 q が存在する状態 絶対値は aq で 負電荷 q から正電荷 q へ向かうベクトルである 例えば 水分子は下右図のような向きの電気双極子モーメントをもち その大きさは約 1.85D である このように元々から持っている双極子モーメントを
1/1/6 9 章分子物性 1 節電気双極子モーメント (Electric Dipole Moment) 電子双極子モーメント とは 微小な距離 a だけ離れて点電荷 q が存在する状態 絶対値は aq で 負電荷 q から正電荷 q へ向かうベクトルである 例えば 水分子は下右図のような向きの電気双極子モーメントをもち その大きさは約 1.85D である このように元々から持っている双極子モーメントを
Microsoft Word - Chap17
 第 7 章化学反応に対する磁場効果における三重項機構 その 7.. 節の訂正 年 7 月 日. 節 章の9ページ の赤枠に記載した説明は間違いであった事に気付いた 以下に訂正する しかし.. 式は 結果的には正しいので安心して下さい 磁場 の存在下でのT 状態のハミルトニアン は ゼーマン項 と時間に依存するスピン-スピン相互作用の項 との和となる..=7.. g S = g S z = S z g
第 7 章化学反応に対する磁場効果における三重項機構 その 7.. 節の訂正 年 7 月 日. 節 章の9ページ の赤枠に記載した説明は間違いであった事に気付いた 以下に訂正する しかし.. 式は 結果的には正しいので安心して下さい 磁場 の存在下でのT 状態のハミルトニアン は ゼーマン項 と時間に依存するスピン-スピン相互作用の項 との和となる..=7.. g S = g S z = S z g
PowerPoint Presentation
 付録 2 2 次元アフィン変換 直交変換 たたみ込み 1.2 次元のアフィン変換 座標 (x,y ) を (x,y) に移すことを 2 次元での変換. 特に, 変換が と書けるとき, アフィン変換, アフィン変換は, その 1 次の項による変換 と 0 次の項による変換 アフィン変換 0 次の項は平行移動 1 次の項は座標 (x, y ) をベクトルと考えて とすれば このようなもの 2 次元ベクトルの線形写像
付録 2 2 次元アフィン変換 直交変換 たたみ込み 1.2 次元のアフィン変換 座標 (x,y ) を (x,y) に移すことを 2 次元での変換. 特に, 変換が と書けるとき, アフィン変換, アフィン変換は, その 1 次の項による変換 と 0 次の項による変換 アフィン変換 0 次の項は平行移動 1 次の項は座標 (x, y ) をベクトルと考えて とすれば このようなもの 2 次元ベクトルの線形写像
Microsoft PowerPoint - 10.pptx
 0. 固有値とその応用 固有値と固有ベクトル 2 行列による写像から固有ベクトルへ m n A : m n n m 行列によって線形写像 f R R A が表せることを見てきた ここでは 2 次元平面の行列による写像を調べる 2 = 2 A 2 2 とし 写像 まず 単位ベクトルの像を求める u 2 x = v 2 y f : R A R を考える u 2 2 u, 2 2 0 = = v 2 0
0. 固有値とその応用 固有値と固有ベクトル 2 行列による写像から固有ベクトルへ m n A : m n n m 行列によって線形写像 f R R A が表せることを見てきた ここでは 2 次元平面の行列による写像を調べる 2 = 2 A 2 2 とし 写像 まず 単位ベクトルの像を求める u 2 x = v 2 y f : R A R を考える u 2 2 u, 2 2 0 = = v 2 0
多体系の量子力学 ー同種の多体系ー
 スピンに依存する有効相互作用の発現と化学結合のしくみ 巨視的な物体の構造にとって 基本的な単位になるのは原子または分子であり 物性の基礎にあるのは原子または分子の性質である. ボルン オッペンハイマー近似. He 原子中の 電子状態 ( 中心 電子系 ) 外場の中の同種 粒子系ー. 電子間相互作用のない場合. 電子間相互作用がある場合.3 電子系の波動関数は全反対称.4 電子系のスピン演算子の固有関数と対称性.5
スピンに依存する有効相互作用の発現と化学結合のしくみ 巨視的な物体の構造にとって 基本的な単位になるのは原子または分子であり 物性の基礎にあるのは原子または分子の性質である. ボルン オッペンハイマー近似. He 原子中の 電子状態 ( 中心 電子系 ) 外場の中の同種 粒子系ー. 電子間相互作用のない場合. 電子間相互作用がある場合.3 電子系の波動関数は全反対称.4 電子系のスピン演算子の固有関数と対称性.5
Microsoft Word - 素粒子物理学I.doc
 6. 自発的対称性の破れとヒッグス機構 : 素粒子の標準模型 Dc 方程式.5 を導くラグランジアンは ϕ ϕ mϕϕ 6. である [H] Eu-nn 方程式 を使って 6. のラグランジア ンから Dc 方程式が導かれることを示せ 6. ゲージ対称性 6.. U 対称性 :QED ディラック粒子の複素場 ψに対する位相変換 ϕ ϕ 6. に対して ラグランジアンが不変であることを要請する これは簡単に示せる
6. 自発的対称性の破れとヒッグス機構 : 素粒子の標準模型 Dc 方程式.5 を導くラグランジアンは ϕ ϕ mϕϕ 6. である [H] Eu-nn 方程式 を使って 6. のラグランジア ンから Dc 方程式が導かれることを示せ 6. ゲージ対称性 6.. U 対称性 :QED ディラック粒子の複素場 ψに対する位相変換 ϕ ϕ 6. に対して ラグランジアンが不変であることを要請する これは簡単に示せる
Microsoft Word - note02.doc
 年度 物理化学 Ⅱ 講義ノート. 二原子分子の振動. 調和振動子近似 モデル 分子 = 理想的なバネでつながった原子 r : 核間距離, r e : 平衡核間距離, : 変位 ( = r r e ), k f : 力の定数ポテンシャルエネルギー ( ) k V = f (.) 古典運動方程式 [ 振動数 ] 3.3 d kf (.) dt μ : 換算質量 (m, m : 原子, の質量 ) mm
年度 物理化学 Ⅱ 講義ノート. 二原子分子の振動. 調和振動子近似 モデル 分子 = 理想的なバネでつながった原子 r : 核間距離, r e : 平衡核間距離, : 変位 ( = r r e ), k f : 力の定数ポテンシャルエネルギー ( ) k V = f (.) 古典運動方程式 [ 振動数 ] 3.3 d kf (.) dt μ : 換算質量 (m, m : 原子, の質量 ) mm
解析力学B - 第11回: 正準変換
 解析力学 B 第 11 回 : 正準変換 神戸大 : 陰山聡 ホームページ ( 第 6 回から今回までの講義ノート ) http://tinyurl.com/kage2010 2011.01.27 正準変換 バネ問題 ( あえて下手に座標をとった ) ハミルトニアンを考える q 正準方程式は H = p2 2m + k 2 (q l 0) 2 q = H p = p m ṗ = H q = k(q
解析力学 B 第 11 回 : 正準変換 神戸大 : 陰山聡 ホームページ ( 第 6 回から今回までの講義ノート ) http://tinyurl.com/kage2010 2011.01.27 正準変換 バネ問題 ( あえて下手に座標をとった ) ハミルトニアンを考える q 正準方程式は H = p2 2m + k 2 (q l 0) 2 q = H p = p m ṗ = H q = k(q
Microsoft PowerPoint _量子力学短大.pptx
 . エネルギーギャップとrllouゾーン ブリルアン領域,t_8.. 周期ポテンシャル中の電子とエネルギーギャップ 簡単のため 次元に間隔 で原子が並んでいる結晶を考える 右方向に進行している電子の波は 間隔 で規則正しく並んでいる原子が作る格子によって散乱され 左向きに進行する波となる 波長 λ が の時 r の反射条件 式を満たし 両者の波が互いに強め合い 定在波を作る つまり 式 式を満たす波は
. エネルギーギャップとrllouゾーン ブリルアン領域,t_8.. 周期ポテンシャル中の電子とエネルギーギャップ 簡単のため 次元に間隔 で原子が並んでいる結晶を考える 右方向に進行している電子の波は 間隔 で規則正しく並んでいる原子が作る格子によって散乱され 左向きに進行する波となる 波長 λ が の時 r の反射条件 式を満たし 両者の波が互いに強め合い 定在波を作る つまり 式 式を満たす波は
1/12 平成 29 年 3 月 24 日午後 1 時 1 分第 3 章測地線 第 3 章測地線 Ⅰ. 変分法と運動方程式最小作用の原理に基づくラグランジュの方法により 重力場中の粒子の運動方程式が求められる これは 力が未知の時に有効な方法であり 今のような 一般相対性理論における力を求めるのに使
 / 平成 9 年 3 月 4 日午後 時 分第 3 章測地線 第 3 章測地線 Ⅰ. 変分法と運動方程式最小作用の原理に基づくラグランジュの方法により 重力場中の粒子の運動方程式が求められる これは 力が未知の時に有効な方法であり 今のような 一般相対性理論における力を求めるのに使う事ができる 最小作用の原理 : 粒子が時刻 から の間に移動したとき 位置 と速度 v = するのが ラグランジュ関数
/ 平成 9 年 3 月 4 日午後 時 分第 3 章測地線 第 3 章測地線 Ⅰ. 変分法と運動方程式最小作用の原理に基づくラグランジュの方法により 重力場中の粒子の運動方程式が求められる これは 力が未知の時に有効な方法であり 今のような 一般相対性理論における力を求めるのに使う事ができる 最小作用の原理 : 粒子が時刻 から の間に移動したとき 位置 と速度 v = するのが ラグランジュ関数
例 e 指数関数的に減衰する信号を h( a < + a a すると, それらのラプラス変換は, H ( ) { e } e インパルス応答が h( a < ( ただし a >, U( ) { } となるシステムにステップ信号 ( y( のラプラス変換 Y () は, Y ( ) H ( ) X (
 第 週ラプラス変換 教科書 p.34~ 目標ラプラス変換の定義と意味を理解する フーリエ変換や Z 変換と並ぶ 信号解析やシステム設計における重要なツール ラプラス変換は波動現象や電気回路など様々な分野で 微分方程式を解くために利用されてきた ラプラス変換を用いることで微分方程式は代数方程式に変換される また 工学上使われる主要な関数のラプラス変換は簡単な形の関数で表されるので これを ラプラス変換表
第 週ラプラス変換 教科書 p.34~ 目標ラプラス変換の定義と意味を理解する フーリエ変換や Z 変換と並ぶ 信号解析やシステム設計における重要なツール ラプラス変換は波動現象や電気回路など様々な分野で 微分方程式を解くために利用されてきた ラプラス変換を用いることで微分方程式は代数方程式に変換される また 工学上使われる主要な関数のラプラス変換は簡単な形の関数で表されるので これを ラプラス変換表
平成 年 月 7 日 ( 土 第 75 回数学教育実践研究会アスティ 45 ビル F セミナールーム A 札幌医科大学 年 P ab, を正の定数とする 平面上において ( a, を中心とする円 Q 4 C と (, b を中心とする円 C が 原点 O で外接している また P を円 C 上の点と
 平成 年 月 7 日 ( 土 第 75 回数学教育実践研究会アスティ 45 ビル F セミナールーム 微分積分の拡張 変数関数問題へのアプローチ 予選決勝優勝法からラグランジュ未定乗数法 松本睦郎 ( 札幌北高等学校 変数関数の最大値 最小値に関する問題には多様なアプローチ法がある 文字を固定した 予選決勝優勝法, 計算のみで解法する 文字消去法, 微分積分を利用した ラグランジュ未定乗数法 がある
平成 年 月 7 日 ( 土 第 75 回数学教育実践研究会アスティ 45 ビル F セミナールーム 微分積分の拡張 変数関数問題へのアプローチ 予選決勝優勝法からラグランジュ未定乗数法 松本睦郎 ( 札幌北高等学校 変数関数の最大値 最小値に関する問題には多様なアプローチ法がある 文字を固定した 予選決勝優勝法, 計算のみで解法する 文字消去法, 微分積分を利用した ラグランジュ未定乗数法 がある
Probit , Mixed logit
 Probit, Mixed logit 2016/5/16 スタートアップゼミ #5 B4 後藤祥孝 1 0. 目次 Probit モデルについて 1. モデル概要 2. 定式化と理解 3. 推定 Mixed logit モデルについて 4. モデル概要 5. 定式化と理解 6. 推定 2 1.Probit 概要 プロビットモデルとは. 効用関数の誤差項に多変量正規分布を仮定したもの. 誤差項には様々な要因が存在するため,
Probit, Mixed logit 2016/5/16 スタートアップゼミ #5 B4 後藤祥孝 1 0. 目次 Probit モデルについて 1. モデル概要 2. 定式化と理解 3. 推定 Mixed logit モデルについて 4. モデル概要 5. 定式化と理解 6. 推定 2 1.Probit 概要 プロビットモデルとは. 効用関数の誤差項に多変量正規分布を仮定したもの. 誤差項には様々な要因が存在するため,
<4D F736F F D E4F8E9F82C982A882AF82E98D7397F1>
 3 三次における行列 要旨高校では ほとんど 2 2 の正方行列しか扱ってなく 三次の正方行列について考えてみたかったため 数 C で学んだ定理を三次の正方行列に応用して 自分たちで仮説を立てて求めていったら 空間における回転移動を表す行列 三次のケーリー ハミルトンの定理 三次における逆行列を求めたり 仮説をたてることができた. 目的 数 C で学んだ定理を三次の正方行列に応用する 2. 概要目的の到達点として
3 三次における行列 要旨高校では ほとんど 2 2 の正方行列しか扱ってなく 三次の正方行列について考えてみたかったため 数 C で学んだ定理を三次の正方行列に応用して 自分たちで仮説を立てて求めていったら 空間における回転移動を表す行列 三次のケーリー ハミルトンの定理 三次における逆行列を求めたり 仮説をたてることができた. 目的 数 C で学んだ定理を三次の正方行列に応用する 2. 概要目的の到達点として
1/17 平成 29 年 3 月 25 日 ( 土 ) 午前 11 時 1 分量子力学とクライン ゴルドン方程式 ( 学部 3 年次秋学期向 ) 量子力学とクライン ゴルドン方程式 素粒子の満たす場 y ( x,t) の運動方程式 : クライン ゴルドン方程式 : æ 3 ö ç å è m= 0
 /7 平成 9 年 月 5 日 ( 土 午前 時 分量子力学とクライン ゴルドン方程式 ( 学部 年次秋学期向 量子力学とクライン ゴルドン方程式 素粒子の満たす場 (,t の運動方程式 : クライン ゴルドン方程式 : æ ö ç å è = 0 c + ( t =, 0 (. = 0 ì æ = = = ö æ ö æ ö ç ì =,,,,,,, ç 0 = ç Ñ 0 = ç Ñ 0 Ñ Ñ
/7 平成 9 年 月 5 日 ( 土 午前 時 分量子力学とクライン ゴルドン方程式 ( 学部 年次秋学期向 量子力学とクライン ゴルドン方程式 素粒子の満たす場 (,t の運動方程式 : クライン ゴルドン方程式 : æ ö ç å è = 0 c + ( t =, 0 (. = 0 ì æ = = = ö æ ö æ ö ç ì =,,,,,,, ç 0 = ç Ñ 0 = ç Ñ 0 Ñ Ñ
Microsoft Word - thesis.doc
 剛体の基礎理論 -. 剛体の基礎理論初めに本論文で大域的に使用する記号を定義する. 使用する記号トルク撃力力角運動量角速度姿勢対角化された慣性テンソル慣性テンソル運動量速度位置質量時間 J W f F P p .. 質点の並進運動 質点は位置 と速度 P を用いる. ニュートンの運動方程式 という状態を持つ. 但し ここでは速度ではなく運動量 F P F.... より質点の運動は既に明らかであり 質点の状態ベクトル
剛体の基礎理論 -. 剛体の基礎理論初めに本論文で大域的に使用する記号を定義する. 使用する記号トルク撃力力角運動量角速度姿勢対角化された慣性テンソル慣性テンソル運動量速度位置質量時間 J W f F P p .. 質点の並進運動 質点は位置 と速度 P を用いる. ニュートンの運動方程式 という状態を持つ. 但し ここでは速度ではなく運動量 F P F.... より質点の運動は既に明らかであり 質点の状態ベクトル
DVIOUT
 最適レギュレータ 松尾研究室資料 第 最適レギュレータ 節時不変型無限時間最適レギュレータ 状態フィードバックの可能な場合の無限時間問題における最適レギュレータについて確定系について説明する. ここで, レギュレータとは状態量をゼロにするようなコントローラのことである. なぜ, 無限時間問題のみを述べるかという理由は以下のとおりである. 有限時間の最適レギュレータ問題の場合の最適フィードバックゲインは微分方程式の解から構成される時間関数として表現される.
最適レギュレータ 松尾研究室資料 第 最適レギュレータ 節時不変型無限時間最適レギュレータ 状態フィードバックの可能な場合の無限時間問題における最適レギュレータについて確定系について説明する. ここで, レギュレータとは状態量をゼロにするようなコントローラのことである. なぜ, 無限時間問題のみを述べるかという理由は以下のとおりである. 有限時間の最適レギュレータ問題の場合の最適フィードバックゲインは微分方程式の解から構成される時間関数として表現される.
2_分子軌道法解説
 2. 分子軌道法解説 分子軌道法計算を行ってその結果を正しく理解するには, 計算の背景となる理論を勉強 する必要がある この演習では詳細を講義する時間的な余裕がないので, それはいろいろ な講義を通しておいおい学んで頂くこととして, ここではその概要をごく簡単に説明しよう 2.1 原子軌道原子はその質量のほとんどすべてを占める原子核と, その周囲をまわっている何個かの電子からなっている 原子核は最も軽い水素の場合でも電子の約
2. 分子軌道法解説 分子軌道法計算を行ってその結果を正しく理解するには, 計算の背景となる理論を勉強 する必要がある この演習では詳細を講義する時間的な余裕がないので, それはいろいろ な講義を通しておいおい学んで頂くこととして, ここではその概要をごく簡単に説明しよう 2.1 原子軌道原子はその質量のほとんどすべてを占める原子核と, その周囲をまわっている何個かの電子からなっている 原子核は最も軽い水素の場合でも電子の約
Microsoft PowerPoint - 第2回半導体工学
 17 年 1 月 16 日 月 1 限 8:5~1:15 IB15 第 回半導体工学 * バンド構造と遷移確率 天野浩 項目 1 章量子論入門 何故 Si は光らず GN は良く光るのか? *MOSFET ゲート SiO / チャネル Si 界面の量子輸送過程 MOSFET には どのようなゲート材料が必要なのか? http://www.iue.tuwien.c.t/ph/vsicek/noe3.html
17 年 1 月 16 日 月 1 限 8:5~1:15 IB15 第 回半導体工学 * バンド構造と遷移確率 天野浩 項目 1 章量子論入門 何故 Si は光らず GN は良く光るのか? *MOSFET ゲート SiO / チャネル Si 界面の量子輸送過程 MOSFET には どのようなゲート材料が必要なのか? http://www.iue.tuwien.c.t/ph/vsicek/noe3.html
物性基礎
 水素様原子 水素原子 水素様原子 エネルギー固有値 波動関数 主量子数 角運動量 方位量子数 磁気量子数 原子核 + 電子 個 F p F = V = 水素様原子 古典力学 水素様原子 量子力学 角運動量 L p F p L 運動方程式 d dt p = d d d p p = p + dt dt dt = p p = d dt L = 角運動量の保存則 ポテンシャルエネルギー V = 4πε =
水素様原子 水素原子 水素様原子 エネルギー固有値 波動関数 主量子数 角運動量 方位量子数 磁気量子数 原子核 + 電子 個 F p F = V = 水素様原子 古典力学 水素様原子 量子力学 角運動量 L p F p L 運動方程式 d dt p = d d d p p = p + dt dt dt = p p = d dt L = 角運動量の保存則 ポテンシャルエネルギー V = 4πε =
パソコンシミュレータの現状
 第 2 章微分 偏微分, 写像 豊橋技術科学大学森謙一郎 2. 連続関数と微分 工学において物理現象を支配する方程式は微分方程式で表されていることが多く, 有限要素法も微分方程式を解く数値解析法であり, 定式化においては微分 積分が一般的に用いられており. 数学の基礎知識が必要になる. 図 2. に示すように, 微分は連続な関数 f() の傾きを求めることであり, 微小な に対して傾きを表し, を無限に
第 2 章微分 偏微分, 写像 豊橋技術科学大学森謙一郎 2. 連続関数と微分 工学において物理現象を支配する方程式は微分方程式で表されていることが多く, 有限要素法も微分方程式を解く数値解析法であり, 定式化においては微分 積分が一般的に用いられており. 数学の基礎知識が必要になる. 図 2. に示すように, 微分は連続な関数 f() の傾きを求めることであり, 微小な に対して傾きを表し, を無限に
数学 t t t t t 加法定理 t t t 倍角公式加法定理で α=β と置く. 三角関数
 . 三角関数 基本関係 t cot c sc c cot sc t 還元公式 t t t t t t cot t cot t 数学 数学 t t t t t 加法定理 t t t 倍角公式加法定理で α=β と置く. 三角関数 数学. 三角関数 5 積和公式 6 和積公式 数学. 三角関数 7 合成 t V v t V v t V V V V VV V V V t V v v 8 べき乗 5 6 6
. 三角関数 基本関係 t cot c sc c cot sc t 還元公式 t t t t t t cot t cot t 数学 数学 t t t t t 加法定理 t t t 倍角公式加法定理で α=β と置く. 三角関数 数学. 三角関数 5 積和公式 6 和積公式 数学. 三角関数 7 合成 t V v t V v t V V V V VV V V V t V v v 8 べき乗 5 6 6
Microsoft Word - 補論3.2
 補論 3. 多変量 GARC モデル 07//6 新谷元嗣 藪友良 対数尤度関数 3 章 7 節では 変量の対数尤度を求めた ここでは多変量の場合 とくに 変量について対数尤度を求める 誤差項 は平均 0 で 次元の正規分布に従うとする 単純化のため 分散と共分散は時間を通じて一定としよう ( この仮定は後で変更される ) したがって ij から添え字 を除くことができる このとき と の尤度関数は
補論 3. 多変量 GARC モデル 07//6 新谷元嗣 藪友良 対数尤度関数 3 章 7 節では 変量の対数尤度を求めた ここでは多変量の場合 とくに 変量について対数尤度を求める 誤差項 は平均 0 で 次元の正規分布に従うとする 単純化のため 分散と共分散は時間を通じて一定としよう ( この仮定は後で変更される ) したがって ij から添え字 を除くことができる このとき と の尤度関数は
数値計算で学ぶ物理学 4 放物運動と惑星運動 地上のように下向きに重力がはたらいているような場においては 物体を投げると放物運動をする 一方 中心星のまわりの重力場中では 惑星は 円 だ円 放物線または双曲線を描きながら運動する ここでは 放物運動と惑星運動を 運動方程式を導出したうえで 数値シミュ
 数値計算で学ぶ物理学 4 放物運動と惑星運動 地上のように下向きに重力がはたらいているような場においては 物体を投げると放物運動をする 一方 中心星のまわりの重力場中では 惑星は 円 だ円 放物線または双曲線を描きながら運動する ここでは 放物運動と惑星運動を 運動方程式を導出したうえで 数値シミュレーションによって計算してみる 4.1 放物運動一様な重力場における放物運動を考える 一般に質量の物体に作用する力をとすると運動方程式は
数値計算で学ぶ物理学 4 放物運動と惑星運動 地上のように下向きに重力がはたらいているような場においては 物体を投げると放物運動をする 一方 中心星のまわりの重力場中では 惑星は 円 だ円 放物線または双曲線を描きながら運動する ここでは 放物運動と惑星運動を 運動方程式を導出したうえで 数値シミュレーションによって計算してみる 4.1 放物運動一様な重力場における放物運動を考える 一般に質量の物体に作用する力をとすると運動方程式は
Microsoft PowerPoint - qchem3-12
 8 年度冬学期 量子化学 Ⅲ 3 章全体のまとめ 9 年 月 日 担当 : 常田貴夫准教授 主要テーマの変遷 年主要テーマ理論化学のトピック科学技術のトピック 196 1937 量子力学の基礎理論構築 HF 法 経験法 V 法 摂動法 固体論 反応論など 1938 1949 原子爆弾関連反応速度論など 195-196 1961-1968 1969-1984 1985-1995 1996 5 量子論
8 年度冬学期 量子化学 Ⅲ 3 章全体のまとめ 9 年 月 日 担当 : 常田貴夫准教授 主要テーマの変遷 年主要テーマ理論化学のトピック科学技術のトピック 196 1937 量子力学の基礎理論構築 HF 法 経験法 V 法 摂動法 固体論 反応論など 1938 1949 原子爆弾関連反応速度論など 195-196 1961-1968 1969-1984 1985-1995 1996 5 量子論
Microsoft Word - 1-4Wd
 第 4 章運動範囲が制限された電子の Scrödinger 方程式の解とその解釈原子 分子の中の電子の運動は原子核の正の電荷によって制約を受けています. 運動範囲が制限された電子はどのような行動をとるか を Scrödinger 方程式を解いて調べましょう. 具体的には, 箱 に閉じ込められた電子の問題です ( 図 1-5). この問題は簡単な系についての Scrödinger 方程式のとき方の例であると同時に量子論の本質が含まれています.
第 4 章運動範囲が制限された電子の Scrödinger 方程式の解とその解釈原子 分子の中の電子の運動は原子核の正の電荷によって制約を受けています. 運動範囲が制限された電子はどのような行動をとるか を Scrödinger 方程式を解いて調べましょう. 具体的には, 箱 に閉じ込められた電子の問題です ( 図 1-5). この問題は簡単な系についての Scrödinger 方程式のとき方の例であると同時に量子論の本質が含まれています.
Microsoft Word - Chap11
 第 章 次元回転群とそのリー代数. SO のリー代数. 節でリー代数を定義したが 以下にその定義を再録する なお 多くの教科書に従って本章以降は ep t A の代わりに ep t と書くこととする 定義.. G を 次の線型リー群とすると 任意の実数 t に対して ep t G となる gl C の全体をGのリー代数 またはリー環 という 例えば ep t が 次の特殊直交群 SO の元であれば
第 章 次元回転群とそのリー代数. SO のリー代数. 節でリー代数を定義したが 以下にその定義を再録する なお 多くの教科書に従って本章以降は ep t A の代わりに ep t と書くこととする 定義.. G を 次の線型リー群とすると 任意の実数 t に対して ep t G となる gl C の全体をGのリー代数 またはリー環 という 例えば ep t が 次の特殊直交群 SO の元であれば
スライド 1
 暫定版修正 加筆の可能性あり ( 付録 ) 電磁波 ( 光 ) の角運動量. 復習 : 電磁波 ( 光 ) のエネルギー. 運動量 角運動量 ( 実空間 ) 3. 軌道 スピン角運動量 4. 円偏光状態 5. 螺旋状態 付録 8 のアプローチ. 本付録では電磁波 ( 光 ) の軌道 スピン角運動量ついて古典的に扱う. スピン角運動量は直線偏光状態では零 円偏光状態では非零 右 左回りで大きさは同じ
暫定版修正 加筆の可能性あり ( 付録 ) 電磁波 ( 光 ) の角運動量. 復習 : 電磁波 ( 光 ) のエネルギー. 運動量 角運動量 ( 実空間 ) 3. 軌道 スピン角運動量 4. 円偏光状態 5. 螺旋状態 付録 8 のアプローチ. 本付録では電磁波 ( 光 ) の軌道 スピン角運動量ついて古典的に扱う. スピン角運動量は直線偏光状態では零 円偏光状態では非零 右 左回りで大きさは同じ
1/17 平成 29 年 3 月 25 日 ( 土 ) 午前 11 時 37 分第 7 章 : 量子力学とディラック方程式 ( 学部 4 年次向 ) 第 7 章量子力学とディラック方程式 Ⅰ. クライン ゴルドン方程式の完全平方化 素粒子場 : y ( x,t ) の従うクライン ゴルドン方程式は
 /7 平成 9 年 月 5 日 ( 土 ) 午前 時 7 分第 7 章 : 量子力学とディラック方程式 ( 学部 4 年次向 ) 第 7 章量子力学とディラック方程式 Ⅰ. クライン ゴルドン方程式の完全平方化 素粒子場 : y ( x,t ) の従うクライン ゴルドン方程式は 素粒子を質量 とすると ì x : ( ct, x, y, z) :,,, ì c ct ç + y (, t) ç å
/7 平成 9 年 月 5 日 ( 土 ) 午前 時 7 分第 7 章 : 量子力学とディラック方程式 ( 学部 4 年次向 ) 第 7 章量子力学とディラック方程式 Ⅰ. クライン ゴルドン方程式の完全平方化 素粒子場 : y ( x,t ) の従うクライン ゴルドン方程式は 素粒子を質量 とすると ì x : ( ct, x, y, z) :,,, ì c ct ç + y (, t) ç å
多変量解析 ~ 重回帰分析 ~ 2006 年 4 月 21 日 ( 金 ) 南慶典
 多変量解析 ~ 重回帰分析 ~ 2006 年 4 月 21 日 ( 金 ) 南慶典 重回帰分析とは? 重回帰分析とは複数の説明変数から目的変数との関係性を予測 評価説明変数 ( 数量データ ) は目的変数を説明するのに有効であるか得られた関係性より未知のデータの妥当性を判断する これを重回帰分析という つまり どんなことをするのか? 1 最小 2 乗法により重回帰モデルを想定 2 自由度調整済寄与率を求め
多変量解析 ~ 重回帰分析 ~ 2006 年 4 月 21 日 ( 金 ) 南慶典 重回帰分析とは? 重回帰分析とは複数の説明変数から目的変数との関係性を予測 評価説明変数 ( 数量データ ) は目的変数を説明するのに有効であるか得られた関係性より未知のデータの妥当性を判断する これを重回帰分析という つまり どんなことをするのか? 1 最小 2 乗法により重回帰モデルを想定 2 自由度調整済寄与率を求め
Matrix and summation convention Kronecker delta δ ij 1 = 0 ( i = j) ( i j) permutation symbol e ijk = (even permutation) (odd permutation) (othe
 Matr ad summato covto Krockr dlta δ ( ) ( ) prmutato symbol k (v prmutato) (odd prmutato) (othrs) gvalu dtrmat dt 6 k rst r s kt opyrght s rsrvd. No part of ths documt may b rproducd for proft. 行列 行 正方行列
Matr ad summato covto Krockr dlta δ ( ) ( ) prmutato symbol k (v prmutato) (odd prmutato) (othrs) gvalu dtrmat dt 6 k rst r s kt opyrght s rsrvd. No part of ths documt may b rproducd for proft. 行列 行 正方行列
ベイズ統計入門
 ベイズ統計入門 条件付確率 事象 F が起こったことが既知であるという条件の下で E が起こる確率を条件付確率 (codtoal probablt) という P ( E F ) P ( E F ) P( F ) 定義式を変形すると 確率の乗法公式となる ( E F ) P( F ) P( E F ) P( E) P( F E) P 事象の独立 ある事象の生起する確率が 他のある事象が生起するかどうかによって変化しないとき
ベイズ統計入門 条件付確率 事象 F が起こったことが既知であるという条件の下で E が起こる確率を条件付確率 (codtoal probablt) という P ( E F ) P ( E F ) P( F ) 定義式を変形すると 確率の乗法公式となる ( E F ) P( F ) P( E F ) P( E) P( F E) P 事象の独立 ある事象の生起する確率が 他のある事象が生起するかどうかによって変化しないとき
Microsoft Word - 非線形計画法 原稿
 非線形計画法条件付き最適化問題は目的関数と制約条件で示すが この中に一つでも 次式でないものが含まれる問題を総称して非線形計画法いう 非線形計画問題は 多くの分野で研究されているが 複雑性により十分汎用的なものは確立されておらず 限定的なものに限り幾つかの提案がなされている ここでは簡単な解法について紹介する. 制約なし極値問題 単純問題の解法 変数で表される関数 の極値は を解くことによって求められる
非線形計画法条件付き最適化問題は目的関数と制約条件で示すが この中に一つでも 次式でないものが含まれる問題を総称して非線形計画法いう 非線形計画問題は 多くの分野で研究されているが 複雑性により十分汎用的なものは確立されておらず 限定的なものに限り幾つかの提案がなされている ここでは簡単な解法について紹介する. 制約なし極値問題 単純問題の解法 変数で表される関数 の極値は を解くことによって求められる
Microsoft Word - 1B2011.doc
 第 14 回モールの定理 ( 単純梁の場合 ) ( モールの定理とは何か?p.11) 例題 下記に示す単純梁の C 点のたわみ角 θ C と, たわみ δ C を求めよ ただし, 部材の曲げ 剛性は材軸に沿って一様で とする C D kn B 1.5m 0.5m 1.0m 解答 1 曲げモーメント図を描く,B 点の反力を求める kn kn 4 kn 曲げモーメント図を描く knm 先に得られた曲げモーメントの値を
第 14 回モールの定理 ( 単純梁の場合 ) ( モールの定理とは何か?p.11) 例題 下記に示す単純梁の C 点のたわみ角 θ C と, たわみ δ C を求めよ ただし, 部材の曲げ 剛性は材軸に沿って一様で とする C D kn B 1.5m 0.5m 1.0m 解答 1 曲げモーメント図を描く,B 点の反力を求める kn kn 4 kn 曲げモーメント図を描く knm 先に得られた曲げモーメントの値を
ビジネス統計 統計基礎とエクセル分析 正誤表
 ビジネス統計統計基礎とエクセル分析 ビジネス統計スペシャリスト エクセル分析スペシャリスト 公式テキスト正誤表と学習用データ更新履歴 平成 30 年 5 月 14 日現在 公式テキスト正誤表 頁場所誤正修正 6 知識編第 章 -3-3 最頻値の解説内容 たとえば, 表.1 のデータであれば, 最頻値は 167.5cm というたとえば, 表.1 のデータであれば, 最頻値は 165.0cm ということになります
ビジネス統計統計基礎とエクセル分析 ビジネス統計スペシャリスト エクセル分析スペシャリスト 公式テキスト正誤表と学習用データ更新履歴 平成 30 年 5 月 14 日現在 公式テキスト正誤表 頁場所誤正修正 6 知識編第 章 -3-3 最頻値の解説内容 たとえば, 表.1 のデータであれば, 最頻値は 167.5cm というたとえば, 表.1 のデータであれば, 最頻値は 165.0cm ということになります
<4D F736F F D208CF68BA48C6F8DCF8A C30342C CFA90B68C6F8DCF8A7782CC8AEE967B92E8979D32288F4390B394C529332E646F63>
 2. 厚生経済学の ( 第 ) 基本定理 2 203 年 4 月 7 日 ( 水曜 3 限 )/8 本章では 純粋交換経済において厚生経済学の ( 第 ) 基本定理 が成立することを示す なお より一般的な生産技術のケースについては 4.5 補論 2 で議論する 2. 予算集合と最適消費点 ( 完全 ) 競争市場で達成される資源配分がパレート効率的であることを示すための準備として 個人の最適化行動を検討する
2. 厚生経済学の ( 第 ) 基本定理 2 203 年 4 月 7 日 ( 水曜 3 限 )/8 本章では 純粋交換経済において厚生経済学の ( 第 ) 基本定理 が成立することを示す なお より一般的な生産技術のケースについては 4.5 補論 2 で議論する 2. 予算集合と最適消費点 ( 完全 ) 競争市場で達成される資源配分がパレート効率的であることを示すための準備として 個人の最適化行動を検討する
第9章
 第 9 章光の量子化これまでは光を古典的電磁波として扱い 原子を量子力学システムとして与え 電磁波と原子に束縛された電子との相互作用ポテンシャルを演算子で表現した この表現の中で電磁波の電場はあくまでも古典的パラメータとして振舞う ここでは この電磁波も量子力学的システム ; 電場と磁場をエルミート演算子で与える として表現する その結果 電磁波のエネルギー密度や運動量密度なども演算子として表せれる
第 9 章光の量子化これまでは光を古典的電磁波として扱い 原子を量子力学システムとして与え 電磁波と原子に束縛された電子との相互作用ポテンシャルを演算子で表現した この表現の中で電磁波の電場はあくまでも古典的パラメータとして振舞う ここでは この電磁波も量子力学的システム ; 電場と磁場をエルミート演算子で与える として表現する その結果 電磁波のエネルギー密度や運動量密度なども演算子として表せれる
超伝導状態の輸送方程式におけるゲージ不変性とホール効果
 超伝導状態の輸送方程式におけるゲージ不変性とホール項 輸送方程式について 研究の歴史 微視的導出法 問題点 - 項 超伝導体の 効果の実験 北大 理 物理北孝文 非平衡状態の摂動論 の方法 輸送方程式の微視的導出と問題点 ゲージ不変性とホール項 まとめ バイロイト 月 - 月 カールスルーエ 月 - 月 カールスルーエのお城 モーゼル渓谷 ザルツカンマ - グート ( オーストリア ) バイロイト近郊
超伝導状態の輸送方程式におけるゲージ不変性とホール項 輸送方程式について 研究の歴史 微視的導出法 問題点 - 項 超伝導体の 効果の実験 北大 理 物理北孝文 非平衡状態の摂動論 の方法 輸送方程式の微視的導出と問題点 ゲージ不変性とホール項 まとめ バイロイト 月 - 月 カールスルーエ 月 - 月 カールスルーエのお城 モーゼル渓谷 ザルツカンマ - グート ( オーストリア ) バイロイト近郊
高知工科大学電子 光システム工学科
 卒業研究報告 題 目 量子力学に基づいた水素分子の分子軌道法的取り扱いと Hamiltonian 近似法 指導教員 山本哲也 報告者 山中昭徳 平成 14 年 月 5 日 高知工科大学電子 光システム工学科. 3. 4.1 4. 4.3 4.5 6.6 8.7 10.8 11.9 1.10 1 3. 13 3.113 3. 13 3.3 13 3.4 14 3.5 15 3.6 15 3.7 17
卒業研究報告 題 目 量子力学に基づいた水素分子の分子軌道法的取り扱いと Hamiltonian 近似法 指導教員 山本哲也 報告者 山中昭徳 平成 14 年 月 5 日 高知工科大学電子 光システム工学科. 3. 4.1 4. 4.3 4.5 6.6 8.7 10.8 11.9 1.10 1 3. 13 3.113 3. 13 3.3 13 3.4 14 3.5 15 3.6 15 3.7 17
memo
 数理情報工学特論第一 機械学習とデータマイニング 4 章 : 教師なし学習 3 かしまひさし 鹿島久嗣 ( 数理 6 研 ) kashima@mist.i.~ DEPARTMENT OF MATHEMATICAL INFORMATICS 1 グラフィカルモデルについて学びます グラフィカルモデル グラフィカルラッソ グラフィカルラッソの推定アルゴリズム 2 グラフィカルモデル 3 教師なし学習の主要タスクは
数理情報工学特論第一 機械学習とデータマイニング 4 章 : 教師なし学習 3 かしまひさし 鹿島久嗣 ( 数理 6 研 ) kashima@mist.i.~ DEPARTMENT OF MATHEMATICAL INFORMATICS 1 グラフィカルモデルについて学びます グラフィカルモデル グラフィカルラッソ グラフィカルラッソの推定アルゴリズム 2 グラフィカルモデル 3 教師なし学習の主要タスクは
<4D F736F F D20824F B CC92E8979D814696CA90CF95AA82C691CC90CF95AA2E646F63>
 1/1 平成 23 年 3 月 24 日午後 6 時 52 分 6 ガウスの定理 : 面積分と体積分 6 ガウスの定理 : 面積分と体積分 Ⅰ. 直交座標系 ガウスの定理は 微分して すぐに積分すると元に戻るというルールを 3 次元積分に適用した定理になります よく知っているのは 簡単化のため 変数が1つの場合は dj ( d ( ににします全微分 = 偏微分 d = d = J ( + C d です
1/1 平成 23 年 3 月 24 日午後 6 時 52 分 6 ガウスの定理 : 面積分と体積分 6 ガウスの定理 : 面積分と体積分 Ⅰ. 直交座標系 ガウスの定理は 微分して すぐに積分すると元に戻るというルールを 3 次元積分に適用した定理になります よく知っているのは 簡単化のため 変数が1つの場合は dj ( d ( ににします全微分 = 偏微分 d = d = J ( + C d です
Microsoft PowerPoint - many-particle-quantum-summary090611c
 多体系の量子力学的記述 目次. 量子力学的多粒子系の種類. 粒子系の量子力学 3. 異種の粒子から構成される有限多粒子系 4. 同種粒子の不可識別性 5. スピン自由度をもつ同種の多粒子系の波動関数の ( 位置 スピン ) 交換に対する対称性 6. フェルミ粒子に対するパウリの排他原理 6. 電子の量子状態の占有の仕方 6. スレーター行列式 6.3 どのような場合に 反対称化が重要になるか? 7.
多体系の量子力学的記述 目次. 量子力学的多粒子系の種類. 粒子系の量子力学 3. 異種の粒子から構成される有限多粒子系 4. 同種粒子の不可識別性 5. スピン自由度をもつ同種の多粒子系の波動関数の ( 位置 スピン ) 交換に対する対称性 6. フェルミ粒子に対するパウリの排他原理 6. 電子の量子状態の占有の仕方 6. スレーター行列式 6.3 どのような場合に 反対称化が重要になるか? 7.
Microsoft PowerPoint - H17-5時限(パターン認識).ppt
 パターン認識早稲田大学講義 平成 7 年度 独 産業技術総合研究所栗田多喜夫 赤穂昭太郎 統計的特徴抽出 パターン認識過程 特徴抽出 認識対象から何らかの特徴量を計測 抽出 する必要がある 認識に有効な情報 特徴 を抽出し 次元を縮小した効率の良い空間を構成する過程 文字認識 : スキャナ等で取り込んだ画像から文字の識別に必要な本質的な特徴のみを抽出 例 文字線の傾き 曲率 面積など 識別 与えられた未知の対象を
パターン認識早稲田大学講義 平成 7 年度 独 産業技術総合研究所栗田多喜夫 赤穂昭太郎 統計的特徴抽出 パターン認識過程 特徴抽出 認識対象から何らかの特徴量を計測 抽出 する必要がある 認識に有効な情報 特徴 を抽出し 次元を縮小した効率の良い空間を構成する過程 文字認識 : スキャナ等で取り込んだ画像から文字の識別に必要な本質的な特徴のみを抽出 例 文字線の傾き 曲率 面積など 識別 与えられた未知の対象を
Microsoft PowerPoint - H22制御工学I-10回.ppt
 制御工学 I 第 回 安定性 ラウス, フルビッツの安定判別 平成 年 6 月 日 /6/ 授業の予定 制御工学概論 ( 回 ) 制御技術は現在様々な工学分野において重要な基本技術となっている 工学における制御工学の位置づけと歴史について説明する さらに 制御システムの基本構成と種類を紹介する ラプラス変換 ( 回 ) 制御工学 特に古典制御ではラプラス変換が重要な役割を果たしている ラプラス変換と逆ラプラス変換の定義を紹介し
制御工学 I 第 回 安定性 ラウス, フルビッツの安定判別 平成 年 6 月 日 /6/ 授業の予定 制御工学概論 ( 回 ) 制御技術は現在様々な工学分野において重要な基本技術となっている 工学における制御工学の位置づけと歴史について説明する さらに 制御システムの基本構成と種類を紹介する ラプラス変換 ( 回 ) 制御工学 特に古典制御ではラプラス変換が重要な役割を果たしている ラプラス変換と逆ラプラス変換の定義を紹介し
以下 変数の上のドットは時間に関する微分を表わしている (ex. 2 dx d x x, x 2 dt dt ) 付録 E 非線形微分方程式の平衡点の安定性解析 E-1) 非線形方程式の線形近似特に言及してこなかったが これまでは線形微分方程式 ( x や x, x などがすべて 1 次で なおかつ
 以下 変数の上のドットは時間に関する微分を表わしている (e. d d, dt dt ) 付録 E 非線形微分方程式の平衡点の安定性解析 E-) 非線形方程式の線形近似特に言及してこなかったが これまでは線形微分方程式 ( や, などがすべて 次で なおかつそれらの係数が定数であるような微分方程式 ) に対して安定性の解析を行ってきた しかしながら 実際には非線形の微分方程式で記述される現象も多く存在する
以下 変数の上のドットは時間に関する微分を表わしている (e. d d, dt dt ) 付録 E 非線形微分方程式の平衡点の安定性解析 E-) 非線形方程式の線形近似特に言及してこなかったが これまでは線形微分方程式 ( や, などがすべて 次で なおかつそれらの係数が定数であるような微分方程式 ) に対して安定性の解析を行ってきた しかしながら 実際には非線形の微分方程式で記述される現象も多く存在する
テンソル ( その ) テンソル ( その ) スカラー ( 階のテンソル ) スカラー ( 階のテンソル ) 階数 ベクトル ( 階のテンソル ) ベクトル ( 階のテンソル ) 行列表現 シンボリック表現 [ ]
![テンソル ( その ) テンソル ( その ) スカラー ( 階のテンソル ) スカラー ( 階のテンソル ) 階数 ベクトル ( 階のテンソル ) ベクトル ( 階のテンソル ) 行列表現 シンボリック表現 [ ] テンソル ( その ) テンソル ( その ) スカラー ( 階のテンソル ) スカラー ( 階のテンソル ) 階数 ベクトル ( 階のテンソル ) ベクトル ( 階のテンソル ) 行列表現 シンボリック表現 [ ]](/thumbs/93/113587990.jpg) Tsor th-ordr tsor by dcl xprsso m m Lm m k m k L mk kk quott rul by symbolc xprsso Lk X thrd-ordr tsor cotrcto j j Copyrght s rsrvd. No prt of ths documt my b rproducd for proft. テンソル ( その ) テンソル ( その
Tsor th-ordr tsor by dcl xprsso m m Lm m k m k L mk kk quott rul by symbolc xprsso Lk X thrd-ordr tsor cotrcto j j Copyrght s rsrvd. No prt of ths documt my b rproducd for proft. テンソル ( その ) テンソル ( その
14 化学実験法 II( 吉村 ( 洋 mmol/l の半分だったから さんの測定値は くんの測定値の 4 倍の重みがあり 推定値 としては 0.68 mmol/l その標準偏差は mmol/l 程度ということになる 測定値を 特徴づけるパラメータ t を推定するこの手
 14 化学実験法 II( 吉村 ( 洋 014.6.1. 最小 乗法のはなし 014.6.1. 内容 最小 乗法のはなし...1 最小 乗法の考え方...1 最小 乗法によるパラメータの決定... パラメータの信頼区間...3 重みの異なるデータの取扱い...4 相関係数 決定係数 ( 最小 乗法を語るもう一つの立場...5 実験条件の誤差の影響...5 問題...6 最小 乗法の考え方 飲料水中のカルシウム濃度を
14 化学実験法 II( 吉村 ( 洋 014.6.1. 最小 乗法のはなし 014.6.1. 内容 最小 乗法のはなし...1 最小 乗法の考え方...1 最小 乗法によるパラメータの決定... パラメータの信頼区間...3 重みの異なるデータの取扱い...4 相関係数 決定係数 ( 最小 乗法を語るもう一つの立場...5 実験条件の誤差の影響...5 問題...6 最小 乗法の考え方 飲料水中のカルシウム濃度を
OCW-iダランベールの原理
 講義名連続体力学配布資料 OCW- 第 2 回ダランベールの原理 無機材料工学科准教授安田公一 1 はじめに今回の講義では, まず, 前半でダランベールの原理について説明する これを用いると, 動力学の問題を静力学の問題として解くことができ, さらに, 前回の仮想仕事の原理を適用すると動力学問題も簡単に解くことができるようになる また, 後半では, ダランベールの原理の応用として ラグランジュ方程式の導出を示す
講義名連続体力学配布資料 OCW- 第 2 回ダランベールの原理 無機材料工学科准教授安田公一 1 はじめに今回の講義では, まず, 前半でダランベールの原理について説明する これを用いると, 動力学の問題を静力学の問題として解くことができ, さらに, 前回の仮想仕事の原理を適用すると動力学問題も簡単に解くことができるようになる また, 後半では, ダランベールの原理の応用として ラグランジュ方程式の導出を示す
ボルツマンマシンの高速化
 1. はじめに ボルツマン学習と平均場近似 山梨大学工学部宗久研究室 G04MK016 鳥居圭太 ボルツマンマシンは学習可能な相互結合型ネットワー クの代表的なものである. ボルツマンマシンには, 学習のための統計平均を取る必要があり, 結果を求めるまでに長い時間がかかってしまうという欠点がある. そこで, 学習の高速化のために, 統計を取る2つのステップについて, 以下のことを行う. まず1つ目のステップでは,
1. はじめに ボルツマン学習と平均場近似 山梨大学工学部宗久研究室 G04MK016 鳥居圭太 ボルツマンマシンは学習可能な相互結合型ネットワー クの代表的なものである. ボルツマンマシンには, 学習のための統計平均を取る必要があり, 結果を求めるまでに長い時間がかかってしまうという欠点がある. そこで, 学習の高速化のために, 統計を取る2つのステップについて, 以下のことを行う. まず1つ目のステップでは,
Microsoft PowerPoint - 9.pptx
 9/7/8( 水 9. 線形写像 ここでは 行列の積によって 写像を定義できることをみていく また 行列の積によって定義される写像の性質を調べていく 拡大とスカラー倍 行列演算と写像 ( 次変換 拡大後 k 倍 k 倍 k 倍拡大の関係は スカラー倍を用いて次のように表現できる p = (, ' = k ' 拡大前 p ' = ( ', ' = ( k, k 拡大 4 拡大と行列の積 拡大後 k 倍
9/7/8( 水 9. 線形写像 ここでは 行列の積によって 写像を定義できることをみていく また 行列の積によって定義される写像の性質を調べていく 拡大とスカラー倍 行列演算と写像 ( 次変換 拡大後 k 倍 k 倍 k 倍拡大の関係は スカラー倍を用いて次のように表現できる p = (, ' = k ' 拡大前 p ' = ( ', ' = ( k, k 拡大 4 拡大と行列の積 拡大後 k 倍
スライド タイトルなし
 線形代数 演習 (008 年度版 ) 008/5/6 線形代数 演習 Ⅰ コンピュータ グラフィックス, 次曲面と線形代数指南書第七の巻 直交行列, 実対称行列とその対角化, 次曲線池田勉龍谷大学理工学部数理情報学科 実行列, 正方行列, 実対称行列, 直交行列 a a N A am a MN 実行列 : すべての成分 a が実数である行列 ij ji ij 正方行列 : 行の数と列の数が等しい (
線形代数 演習 (008 年度版 ) 008/5/6 線形代数 演習 Ⅰ コンピュータ グラフィックス, 次曲面と線形代数指南書第七の巻 直交行列, 実対称行列とその対角化, 次曲線池田勉龍谷大学理工学部数理情報学科 実行列, 正方行列, 実対称行列, 直交行列 a a N A am a MN 実行列 : すべての成分 a が実数である行列 ij ji ij 正方行列 : 行の数と列の数が等しい (
数学 ⅡB < 公理 > 公理を論拠に定義を用いて定理を証明する 1 大小関係の公理 順序 (a > b, a = b, a > b 1 つ成立 a > b, b > c a > c 成立 ) 順序と演算 (a > b a + c > b + c (a > b, c > 0 ac > bc) 2 図
 数学 Ⅱ < 公理 > 公理を論拠に定義を用いて定理を証明する 大小関係の公理 順序 >, =, > つ成立 >, > > 成立 順序と演算 > + > + >, > > 図形の公理 平行線の性質 錯角 同位角 三角形の合同条件 三角形の合同相似 量の公理 角の大きさ 線分の長さ < 空間における座漂とベクトル > ベクトルの演算 和 差 実数倍については 文字の計算と同様 ベクトルの成分表示 平面ベクトル
数学 Ⅱ < 公理 > 公理を論拠に定義を用いて定理を証明する 大小関係の公理 順序 >, =, > つ成立 >, > > 成立 順序と演算 > + > + >, > > 図形の公理 平行線の性質 錯角 同位角 三角形の合同条件 三角形の合同相似 量の公理 角の大きさ 線分の長さ < 空間における座漂とベクトル > ベクトルの演算 和 差 実数倍については 文字の計算と同様 ベクトルの成分表示 平面ベクトル
切片 ( 定数項 ) ダミー 以下の単回帰モデルを考えよう これは賃金と就業年数の関係を分析している : ( 賃金関数 ) ここで Y i = α + β X i + u i, i =1,, n, u i ~ i.i.d. N(0, σ 2 ) Y i : 賃金の対数値, X i : 就業年数. (
 統計学ダミー変数による分析 担当 : 長倉大輔 ( ながくらだいすけ ) 1 切片 ( 定数項 ) ダミー 以下の単回帰モデルを考えよう これは賃金と就業年数の関係を分析している : ( 賃金関数 ) ここで Y i = α + β X i + u i, i =1,, n, u i ~ i.i.d. N(0, σ 2 ) Y i : 賃金の対数値, X i : 就業年数. ( 実際は賃金を就業年数だけで説明するのは現実的はない
統計学ダミー変数による分析 担当 : 長倉大輔 ( ながくらだいすけ ) 1 切片 ( 定数項 ) ダミー 以下の単回帰モデルを考えよう これは賃金と就業年数の関係を分析している : ( 賃金関数 ) ここで Y i = α + β X i + u i, i =1,, n, u i ~ i.i.d. N(0, σ 2 ) Y i : 賃金の対数値, X i : 就業年数. ( 実際は賃金を就業年数だけで説明するのは現実的はない
Microsoft PowerPoint - 資料04 重回帰分析.ppt
 04. 重回帰分析 京都大学 加納学 Division of Process Control & Process Sstems Engineering Department of Chemical Engineering, Koto Universit manabu@cheme.koto-u.ac.jp http://www-pse.cheme.koto-u.ac.jp/~kano/ Outline
04. 重回帰分析 京都大学 加納学 Division of Process Control & Process Sstems Engineering Department of Chemical Engineering, Koto Universit manabu@cheme.koto-u.ac.jp http://www-pse.cheme.koto-u.ac.jp/~kano/ Outline
Microsoft PowerPoint - 小路田俊子 [互換モード]
![Microsoft PowerPoint - 小路田俊子 [互換モード] Microsoft PowerPoint - 小路田俊子 [互換モード]](/thumbs/86/94612425.jpg) Wining number in String fiel theory @ 名古屋大学 京大理小路田俊子 畑氏との共同研究 bae on arxiv:.89 内容 開弦の場の理論 Cubic SFT と Chern-Simon 理論の類似性に着目し 位相的不変量である Wining 数を CSFT において実現できるのか調べる S CS k M Wining 数 S N [ g] gg 4 M M
Wining number in String fiel theory @ 名古屋大学 京大理小路田俊子 畑氏との共同研究 bae on arxiv:.89 内容 開弦の場の理論 Cubic SFT と Chern-Simon 理論の類似性に着目し 位相的不変量である Wining 数を CSFT において実現できるのか調べる S CS k M Wining 数 S N [ g] gg 4 M M
DVIOUT-SS_Ma
 第 章 微分方程式 ニュートンはリンゴが落ちるのを見て万有引力を発見した という有名な逸話があります 無重力の宇宙船の中ではリンゴは落ちないで静止していることを考えると 重力が働くと始め静止しているものが動き出して そのスピードはどんどん大きくなる つまり速度の変化が現れることがわかります 速度は一般に時間と共に変化します 速度の瞬間的変化の割合を加速度といい で定義しましょう 速度が変化する, つまり加速度がでなくなるためにはその原因があり
第 章 微分方程式 ニュートンはリンゴが落ちるのを見て万有引力を発見した という有名な逸話があります 無重力の宇宙船の中ではリンゴは落ちないで静止していることを考えると 重力が働くと始め静止しているものが動き出して そのスピードはどんどん大きくなる つまり速度の変化が現れることがわかります 速度は一般に時間と共に変化します 速度の瞬間的変化の割合を加速度といい で定義しましょう 速度が変化する, つまり加速度がでなくなるためにはその原因があり
Chap2.key
 . f( ) V (V V ) V e + V e V V V V ( ) V V ( ) E. - () V (0 ) () V (0 ) () V (0 ) (4) V ( ) E. - () V (0 ) () V (0 ) O r θ ( ) ( ) : (r θ) : { r cos θ r sn θ { r + () V (0 ) (4) V ( ) θ θ arg( ) : π π
. f( ) V (V V ) V e + V e V V V V ( ) V V ( ) E. - () V (0 ) () V (0 ) () V (0 ) (4) V ( ) E. - () V (0 ) () V (0 ) O r θ ( ) ( ) : (r θ) : { r cos θ r sn θ { r + () V (0 ) (4) V ( ) θ θ arg( ) : π π
Microsoft PowerPoint - 9.pptx
 9. 線形写像 ここでは 行列の積によって 写像を定義できることをみていく また 行列の積によって定義される写像の性質を調べていく 行列演算と写像 ( 次変換 3 拡大とスカラー倍 p ' = ( ', ' = ( k, kk p = (, k 倍 k 倍 拡大後 k 倍拡大の関係は スカラー倍を用いて次のように表現できる ' = k ' 拡大前 拡大 4 拡大と行列の積 p ' = ( ', '
9. 線形写像 ここでは 行列の積によって 写像を定義できることをみていく また 行列の積によって定義される写像の性質を調べていく 行列演算と写像 ( 次変換 3 拡大とスカラー倍 p ' = ( ', ' = ( k, kk p = (, k 倍 k 倍 拡大後 k 倍拡大の関係は スカラー倍を用いて次のように表現できる ' = k ' 拡大前 拡大 4 拡大と行列の積 p ' = ( ', '
<4D F736F F F696E74202D2091E6824F82538FCD8CEB82E88C9F8F6F814592F990B382CC8CB4979D82BB82CC82505F D E95848D8682CC90B69
 第 章 誤り検出 訂正の原理 その ブロック符号とその復号 安達文幸 目次 誤り訂正符号化を用いる伝送系誤り検出符号誤り検出 訂正符号 7, ハミング符号, ハミング符号生成行列, パリティ検査行列の一般形符号の生成行列符号の生成行列とパリティ検査行列の関係符号の訂正能力符号多項式 安達 : コミュニケーション符号理論 安達 : コミュニケーション符号理論 誤り訂正符号化を用いる伝送系 伝送システム
第 章 誤り検出 訂正の原理 その ブロック符号とその復号 安達文幸 目次 誤り訂正符号化を用いる伝送系誤り検出符号誤り検出 訂正符号 7, ハミング符号, ハミング符号生成行列, パリティ検査行列の一般形符号の生成行列符号の生成行列とパリティ検査行列の関係符号の訂正能力符号多項式 安達 : コミュニケーション符号理論 安達 : コミュニケーション符号理論 誤り訂正符号化を用いる伝送系 伝送システム
PowerPoint プレゼンテーション
 有効理論を用いた vector like クォーク模型に対する B 中間子稀崩壊からの制限 (Work in progre) 広大院理 高橋隼也 共同研究者 : 広大院理, 広大 CORE-U 広大院理 島根大総合理工 両角卓也 清水勇介 梅枝宏之 導入 標準模型 (SM) のクォーク 標準模型は 6 種類のクォークの存在を仮定 アップタイプ ダウンタイプ u c t d 更にクォークが存在する可能性は?
有効理論を用いた vector like クォーク模型に対する B 中間子稀崩壊からの制限 (Work in progre) 広大院理 高橋隼也 共同研究者 : 広大院理, 広大 CORE-U 広大院理 島根大総合理工 両角卓也 清水勇介 梅枝宏之 導入 標準模型 (SM) のクォーク 標準模型は 6 種類のクォークの存在を仮定 アップタイプ ダウンタイプ u c t d 更にクォークが存在する可能性は?
Information Theory
 前回の復習 講義の概要 chapter 1: 情報を測る... エントロピーの定義 確率変数 X の ( 一次 ) エントロピー M H 1 (X) = p i log 2 p i (bit) i=1 M は実現値の個数,p i は i 番目の実現値が取られる確率 実現値 確率 表 裏 0.5 0.5 H 1 X = 0.5 log 2 0.5 0.5log 2 0.5 = 1bit 1 練習問題の解答
前回の復習 講義の概要 chapter 1: 情報を測る... エントロピーの定義 確率変数 X の ( 一次 ) エントロピー M H 1 (X) = p i log 2 p i (bit) i=1 M は実現値の個数,p i は i 番目の実現値が取られる確率 実現値 確率 表 裏 0.5 0.5 H 1 X = 0.5 log 2 0.5 0.5log 2 0.5 = 1bit 1 練習問題の解答
1/20 平成 29 年 3 月 25 日午前 11 時 7 分第 1 章 :U(N) 群 SU(N) 群 ( 学部 4 年次向 ) 第 1 章 :U(N) 群 SU(N) 群 Ⅰ. 標準模型の素粒子 素粒子の分類図 3 世代 素粒子の標準理論に含まれる素粒子は 素粒子の分類図 から R, G, B
 / 平成 9 年 3 月 5 日午前 時 7 分第 章 :U() 群 SU() 群 ( 学部 4 年次向 ) 第 章 :U() 群 SU() 群 Ⅰ. 標準模型の素粒子 素粒子の分類図 3 世代 素粒子の標準理論に含まれる素粒子は 素粒子の分類図 から R, G, B R, G, B R, G, B u : 5 c :, 6 t :75,e 3 クォーク( quark ) : R, G, B R,
/ 平成 9 年 3 月 5 日午前 時 7 分第 章 :U() 群 SU() 群 ( 学部 4 年次向 ) 第 章 :U() 群 SU() 群 Ⅰ. 標準模型の素粒子 素粒子の分類図 3 世代 素粒子の標準理論に含まれる素粒子は 素粒子の分類図 から R, G, B R, G, B R, G, B u : 5 c :, 6 t :75,e 3 クォーク( quark ) : R, G, B R,
FEM原理講座 (サンプルテキスト)
 サンプルテキスト FEM 原理講座 サイバネットシステム株式会社 8 年 月 9 日作成 サンプルテキストについて 各講師が 講義の内容が伝わりやすいページ を選びました テキストのページは必ずしも連続していません 一部を抜粋しています 幾何光学講座については 実物のテキストではなくガイダンスを掲載いたします 対象とする構造系 物理モデル 連続体 固体 弾性体 / 弾塑性体 / 粘弾性体 / 固体
サンプルテキスト FEM 原理講座 サイバネットシステム株式会社 8 年 月 9 日作成 サンプルテキストについて 各講師が 講義の内容が伝わりやすいページ を選びました テキストのページは必ずしも連続していません 一部を抜粋しています 幾何光学講座については 実物のテキストではなくガイダンスを掲載いたします 対象とする構造系 物理モデル 連続体 固体 弾性体 / 弾塑性体 / 粘弾性体 / 固体
: (a) ( ) A (b) B ( ) A B 11.: (a) x,y (b) r,θ (c) A (x) V A B (x + dx) ( ) ( 11.(a)) dv dt = 0 (11.6) r= θ =
 1 11 11.1 ψ e iα ψ, ψ ψe iα (11.1) *1) L = ψ(x)(γ µ i µ m)ψ(x) ) ( ) ψ e iα(x) ψ(x), ψ(x) ψ(x)e iα(x) (11.3) µ µ + iqa µ (x) (11.4) A µ (x) A µ(x) = A µ (x) + 1 q µα(x) (11.5) 11.1.1 ( ) ( 11.1 ) * 1)
1 11 11.1 ψ e iα ψ, ψ ψe iα (11.1) *1) L = ψ(x)(γ µ i µ m)ψ(x) ) ( ) ψ e iα(x) ψ(x), ψ(x) ψ(x)e iα(x) (11.3) µ µ + iqa µ (x) (11.4) A µ (x) A µ(x) = A µ (x) + 1 q µα(x) (11.5) 11.1.1 ( ) ( 11.1 ) * 1)
2011年度 大阪大・理系数学
 0 大阪大学 ( 理系 ) 前期日程問題 解答解説のページへ a a を自然数とする O を原点とする座標平面上で行列 A= a の表す 次変換 を f とする cosθ siθ () >0 および0θ
0 大阪大学 ( 理系 ) 前期日程問題 解答解説のページへ a a を自然数とする O を原点とする座標平面上で行列 A= a の表す 次変換 を f とする cosθ siθ () >0 および0θ
様々なミクロ計量モデル†
 担当 : 長倉大輔 ( ながくらだいすけ ) この資料は私の講義において使用するために作成した資料です WEB ページ上で公開しており 自由に参照して頂いて構いません ただし 内容について 一応検証してありますが もし間違いがあった場合でもそれによって生じるいかなる損害 不利益について責任を負いかねますのでご了承ください 間違いは発見次第 継続的に直していますが まだ存在する可能性があります 1 カウントデータモデル
担当 : 長倉大輔 ( ながくらだいすけ ) この資料は私の講義において使用するために作成した資料です WEB ページ上で公開しており 自由に参照して頂いて構いません ただし 内容について 一応検証してありますが もし間違いがあった場合でもそれによって生じるいかなる損害 不利益について責任を負いかねますのでご了承ください 間違いは発見次第 継続的に直していますが まだ存在する可能性があります 1 カウントデータモデル
<4D F736F F F696E74202D2091E688EA8CB4979D8C768E5A B8CDD8AB B83685D>
 第一原理計算法の基礎 固体物理からのアプローチを中心に 第一原理計算法とは 原子レベルやナノスケールレベルにおける物質の基本法則である量子力学 ( 第一原理 ) に基づいて, 原子番号だけを入力パラメーターとして, 非経験的に物理機構の解明や物性予測を行う計算手法である. 計算可能な物性値 第一原理計算により, 計算セル ( 原子番号と空間座標既知の原子を含むモデル ) の全エネルギーと電子のエネルギーバンド構造が求まる.
第一原理計算法の基礎 固体物理からのアプローチを中心に 第一原理計算法とは 原子レベルやナノスケールレベルにおける物質の基本法則である量子力学 ( 第一原理 ) に基づいて, 原子番号だけを入力パラメーターとして, 非経験的に物理機構の解明や物性予測を行う計算手法である. 計算可能な物性値 第一原理計算により, 計算セル ( 原子番号と空間座標既知の原子を含むモデル ) の全エネルギーと電子のエネルギーバンド構造が求まる.
Microsoft PowerPoint - e-stat(OLS).pptx
 経済統計学 ( 補足 ) 最小二乗法について 担当 : 小塚匡文 2015 年 11 月 19 日 ( 改訂版 ) 神戸大学経済学部 2015 年度後期開講授業 補足 : 最小二乗法 ( 単回帰分析 ) 1.( 単純 ) 回帰分析とは? 標本サイズTの2 変数 ( ここではXとY) のデータが存在 YをXで説明する回帰方程式を推定するための方法 Y: 被説明変数 ( または従属変数 ) X: 説明変数
経済統計学 ( 補足 ) 最小二乗法について 担当 : 小塚匡文 2015 年 11 月 19 日 ( 改訂版 ) 神戸大学経済学部 2015 年度後期開講授業 補足 : 最小二乗法 ( 単回帰分析 ) 1.( 単純 ) 回帰分析とは? 標本サイズTの2 変数 ( ここではXとY) のデータが存在 YをXで説明する回帰方程式を推定するための方法 Y: 被説明変数 ( または従属変数 ) X: 説明変数
2018年度 2次数学セレクション(微分と積分)
 08 次数学セレクション問題 [ 東京大 ] > 0 とし, f = x - x とおく () x で f ( x ) が単調に増加するための, についての条件を求めよ () 次の 条件を満たす点 (, b) の動きうる範囲を求め, 座標平面上に図示せよ 条件 : 方程式 f = bは相異なる 実数解をもつ 条件 : さらに, 方程式 f = bの解を < < とすると > である -- 08 次数学セレクション問題
08 次数学セレクション問題 [ 東京大 ] > 0 とし, f = x - x とおく () x で f ( x ) が単調に増加するための, についての条件を求めよ () 次の 条件を満たす点 (, b) の動きうる範囲を求め, 座標平面上に図示せよ 条件 : 方程式 f = bは相異なる 実数解をもつ 条件 : さらに, 方程式 f = bの解を < < とすると > である -- 08 次数学セレクション問題
Microsoft PowerPoint - qcomp.ppt [互換モード]
![Microsoft PowerPoint - qcomp.ppt [互換モード] Microsoft PowerPoint - qcomp.ppt [互換モード]](/thumbs/85/91243661.jpg) 量子計算基礎 東京工業大学 河内亮周 概要 計算って何? 数理科学的に 計算 を扱うには 量子力学を計算に使おう! 量子情報とは? 量子情報に対する演算 = 量子計算 一般的な量子回路の構成方法 計算って何? 計算とは? 計算 = 入力情報から出力情報への変換 入力 計算機構 ( デジタルコンピュータ,etc ) 出力 計算とは? 計算 = 入力情報から出力情報への変換 この関数はどれくらい計算が大変か??
量子計算基礎 東京工業大学 河内亮周 概要 計算って何? 数理科学的に 計算 を扱うには 量子力学を計算に使おう! 量子情報とは? 量子情報に対する演算 = 量子計算 一般的な量子回路の構成方法 計算って何? 計算とは? 計算 = 入力情報から出力情報への変換 入力 計算機構 ( デジタルコンピュータ,etc ) 出力 計算とは? 計算 = 入力情報から出力情報への変換 この関数はどれくらい計算が大変か??
Microsoft PowerPoint - 東大講義09-13.ppt [互換モード]
![Microsoft PowerPoint - 東大講義09-13.ppt [互換モード] Microsoft PowerPoint - 東大講義09-13.ppt [互換モード]](/thumbs/88/116773367.jpg) 物性物理学 IA 平成 21 年度前期東京大学大学院講義 東京大学物性研究所高田康民 2009 年 4 月 10 日 -7 月 17 日 (15 回 ) 金曜日 2 時限 (10:15-11:45) 15 11 理学部 1 号館 207 号室 講義は自己充足的 量子力学 ( 第 2 量子化を含む ) 統計力学 場の量子論のごく初歩を仮定 最後の約 10 分間は関連する最先端の研究テーマを雑談風に紹介する
物性物理学 IA 平成 21 年度前期東京大学大学院講義 東京大学物性研究所高田康民 2009 年 4 月 10 日 -7 月 17 日 (15 回 ) 金曜日 2 時限 (10:15-11:45) 15 11 理学部 1 号館 207 号室 講義は自己充足的 量子力学 ( 第 2 量子化を含む ) 統計力学 場の量子論のごく初歩を仮定 最後の約 10 分間は関連する最先端の研究テーマを雑談風に紹介する
ベクトル公式.rtf
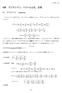 6 章ラプラシアン, ベクトル公式, 定理 6.1 ラプラシアン Laplacian φ はベクトル量である. そこでさらに発散をとると, φ はどういう形になるであろうか? φ = a + a + a φ a + a φ + a φ = φ + φ + φ = 2 φ + 2 φ 2 + 2 φ 2 2 φ = 2 φ 2 + 2 φ 2 + 2 φ 2 = 2 φ したがって,2 階の偏微分演算となる.
6 章ラプラシアン, ベクトル公式, 定理 6.1 ラプラシアン Laplacian φ はベクトル量である. そこでさらに発散をとると, φ はどういう形になるであろうか? φ = a + a + a φ a + a φ + a φ = φ + φ + φ = 2 φ + 2 φ 2 + 2 φ 2 2 φ = 2 φ 2 + 2 φ 2 + 2 φ 2 = 2 φ したがって,2 階の偏微分演算となる.
基礎から学ぶ光物性 第8回 物質と光の相互作用(3) 電子分極の量子論
 基礎から学ぶ光物性第 8 回物質と光の相互作用 (3-1) 第 1 部 : 光スペクトルを量子論で考える 東京農工大学特任教授 佐藤勝昭 第 8 回のはじめに これまでは 光学現象を古典力学の運動方程式で説明してきました この場合 束縛電子系の光学現象は古典的な振動子モデルで扱っていました しかし それでは 光吸収スペクトルの選択則などが説明できません また 半導体や金属のバンド間遷移も扱うことができません
基礎から学ぶ光物性第 8 回物質と光の相互作用 (3-1) 第 1 部 : 光スペクトルを量子論で考える 東京農工大学特任教授 佐藤勝昭 第 8 回のはじめに これまでは 光学現象を古典力学の運動方程式で説明してきました この場合 束縛電子系の光学現象は古典的な振動子モデルで扱っていました しかし それでは 光吸収スペクトルの選択則などが説明できません また 半導体や金属のバンド間遷移も扱うことができません
線積分.indd
 線積分 線積分 ( n, n, n ) (ξ n, η n, ζ n ) ( n-, n-, n- ) (ξ k, η k, ζ k ) ( k, k, k ) ( k-, k-, k- ) 物体に力 を作用させて位置ベクトル A の点 A から位置ベクトル の点 まで曲線 に沿って物体を移動させたときの仕事 W は 次式で計算された A, A, W : d 6 d+ d+ d@,,, d+ d+
線積分 線積分 ( n, n, n ) (ξ n, η n, ζ n ) ( n-, n-, n- ) (ξ k, η k, ζ k ) ( k, k, k ) ( k-, k-, k- ) 物体に力 を作用させて位置ベクトル A の点 A から位置ベクトル の点 まで曲線 に沿って物体を移動させたときの仕事 W は 次式で計算された A, A, W : d 6 d+ d+ d@,,, d+ d+
Microsoft PowerPoint - 卒業論文 pptx
 時間に依存するポテンシャルによる 量子状態の変化 龍谷大学理工学部数理情報学科 T966 二正寺章指導教員飯田晋司 目次 はじめに 次元のシュレーディンガー方程式 3 井戸型ポテンシャルの固有エネルギーと固有関数 4 4 中央に障壁のある井戸型ポテンシャルの固有エネルギーと固有関数 3 5 障壁が時間によって変化する場合 7 6 まとめ 5 一次元のシュレディンガー方程式量子力学の基本方程式 ψ (
時間に依存するポテンシャルによる 量子状態の変化 龍谷大学理工学部数理情報学科 T966 二正寺章指導教員飯田晋司 目次 はじめに 次元のシュレーディンガー方程式 3 井戸型ポテンシャルの固有エネルギーと固有関数 4 4 中央に障壁のある井戸型ポテンシャルの固有エネルギーと固有関数 3 5 障壁が時間によって変化する場合 7 6 まとめ 5 一次元のシュレディンガー方程式量子力学の基本方程式 ψ (
ディジタル信号処理
 ディジタルフィルタの設計法. 逆フィルター. 直線位相 FIR フィルタの設計. 窓関数法による FIR フィルタの設計.5 時間領域での FIR フィルタの設計 3. アナログフィルタを基にしたディジタル IIR フィルタの設計法 I 4. アナログフィルタを基にしたディジタル IIR フィルタの設計法 II 5. 双 次フィルタ LI 離散時間システムの基礎式の証明 [ ] 4. ] [ ]*
ディジタルフィルタの設計法. 逆フィルター. 直線位相 FIR フィルタの設計. 窓関数法による FIR フィルタの設計.5 時間領域での FIR フィルタの設計 3. アナログフィルタを基にしたディジタル IIR フィルタの設計法 I 4. アナログフィルタを基にしたディジタル IIR フィルタの設計法 II 5. 双 次フィルタ LI 離散時間システムの基礎式の証明 [ ] 4. ] [ ]*
PowerPoint Presentation
 応用数学 Ⅱ (7) 7 連立微分方程式の立て方と解法. 高階微分方程式による解法. ベクトル微分方程式による解法 3. 演算子による解法 連立微分方程式 未知数が複数個あり, 未知数の数だけ微分方程式が与えられている場合, これらを連立微分方程式という. d d 解法 () 高階微分方程式化による解法 つの方程式から つの未知数を消去して, 未知数が つの方程式に変換 のみの方程式にするために,
応用数学 Ⅱ (7) 7 連立微分方程式の立て方と解法. 高階微分方程式による解法. ベクトル微分方程式による解法 3. 演算子による解法 連立微分方程式 未知数が複数個あり, 未知数の数だけ微分方程式が与えられている場合, これらを連立微分方程式という. d d 解法 () 高階微分方程式化による解法 つの方程式から つの未知数を消去して, 未知数が つの方程式に変換 のみの方程式にするために,
Microsoft PowerPoint - mp11-06.pptx
 数理計画法第 6 回 塩浦昭義情報科学研究科准教授 shioura@dais.is.tohoku.ac.jp http://www.dais.is.tohoku.ac.jp/~shioura/teaching 第 5 章組合せ計画 5.2 分枝限定法 組合せ計画問題 組合せ計画問題とは : 有限個の もの の組合せの中から, 目的関数を最小または最大にする組合せを見つける問題 例 1: 整数計画問題全般
数理計画法第 6 回 塩浦昭義情報科学研究科准教授 shioura@dais.is.tohoku.ac.jp http://www.dais.is.tohoku.ac.jp/~shioura/teaching 第 5 章組合せ計画 5.2 分枝限定法 組合せ計画問題 組合せ計画問題とは : 有限個の もの の組合せの中から, 目的関数を最小または最大にする組合せを見つける問題 例 1: 整数計画問題全般
Microsoft PowerPoint - mp11-02.pptx
 数理計画法第 2 回 塩浦昭義情報科学研究科准教授 shioura@dais.is.tohoku.ac.jp http://www.dais.is.tohoku.ac.jp/~shioura/teaching 前回の復習 数理計画とは? 数理計画 ( 復習 ) 数理計画問題とは? 狭義には : 数理 ( 数学 ) を使って計画を立てるための問題 広義には : 与えられた評価尺度に関して最も良い解を求める問題
数理計画法第 2 回 塩浦昭義情報科学研究科准教授 shioura@dais.is.tohoku.ac.jp http://www.dais.is.tohoku.ac.jp/~shioura/teaching 前回の復習 数理計画とは? 数理計画 ( 復習 ) 数理計画問題とは? 狭義には : 数理 ( 数学 ) を使って計画を立てるための問題 広義には : 与えられた評価尺度に関して最も良い解を求める問題
航空機の運動方程式
 可制御性 可観測性. 可制御性システムの状態を, 適切な操作によって, 有限時間内に, 任意の状態から別の任意の状態に移動させることができるか否かという特性を可制御性という. 可制御性を有するシステムに対し, システムは可制御である, 可制御なシステム という言い方をする. 状態方程式, 出力方程式が以下で表されるn 次元 m 入力 r 出力線形時不変システム x Ax u y x Du () に対し,
可制御性 可観測性. 可制御性システムの状態を, 適切な操作によって, 有限時間内に, 任意の状態から別の任意の状態に移動させることができるか否かという特性を可制御性という. 可制御性を有するシステムに対し, システムは可制御である, 可制御なシステム という言い方をする. 状態方程式, 出力方程式が以下で表されるn 次元 m 入力 r 出力線形時不変システム x Ax u y x Du () に対し,
2019 年 6 月 4 日演習問題 I α, β > 0, A > 0 を定数として Cobb-Douglas 型関数 Y = F (K, L) = AK α L β (5) と定義します. (1) F KK, F KL, F LK, F LL を求めましょう. (2) 第 1 象限のすべての点
 09 年 6 月 4 日演習問題 I α, β > 0, A > 0 を定数として Cobb-Douglas 型関数 Y = F K, L) = AK α L β 5) と定義します. ) F KK, F KL, F LK, F LL を求めましょう. ) 第 象限のすべての点 K, L) R ++ に対して F KK K, L) < 0, かつ dethf )K, L) > 0 6) を満たす α,
09 年 6 月 4 日演習問題 I α, β > 0, A > 0 を定数として Cobb-Douglas 型関数 Y = F K, L) = AK α L β 5) と定義します. ) F KK, F KL, F LK, F LL を求めましょう. ) 第 象限のすべての点 K, L) R ++ に対して F KK K, L) < 0, かつ dethf )K, L) > 0 6) を満たす α,
0 部分的最小二乗回帰 Partial Least Squares Regression PLS 明治大学理 学部応用化学科 データ化学 学研究室 弘昌
 0 部分的最小二乗回帰 Parial Leas Squares Regressio PLS 明治大学理 学部応用化学科 データ化学 学研究室 弘昌 部分的最小二乗回帰 (PLS) とは? 部分的最小二乗回帰 (Parial Leas Squares Regressio, PLS) 線形の回帰分析手法の つ 説明変数 ( 記述 ) の数がサンプルの数より多くても計算可能 回帰式を作るときにノイズの影響を受けにくい
0 部分的最小二乗回帰 Parial Leas Squares Regressio PLS 明治大学理 学部応用化学科 データ化学 学研究室 弘昌 部分的最小二乗回帰 (PLS) とは? 部分的最小二乗回帰 (Parial Leas Squares Regressio, PLS) 線形の回帰分析手法の つ 説明変数 ( 記述 ) の数がサンプルの数より多くても計算可能 回帰式を作るときにノイズの影響を受けにくい
スライド 1
 基礎無機化学第 回 分子構造と結合 (IV) 原子価結合法 (II): 昇位と混成 本日のポイント 昇位と混成 s 軌道と p 軌道を混ぜて, 新しい軌道を作る sp 3 混成 : 正四面体型 sp 混成 : 三角形 (p 軌道が つ残る ) sp 混成 : 直線形 (p 軌道が つ残る ) 多重結合との関係炭素などでは以下が基本 ( たまに違う ) 二重結合 sp 混成三重結合 sp 混成 逆に,
基礎無機化学第 回 分子構造と結合 (IV) 原子価結合法 (II): 昇位と混成 本日のポイント 昇位と混成 s 軌道と p 軌道を混ぜて, 新しい軌道を作る sp 3 混成 : 正四面体型 sp 混成 : 三角形 (p 軌道が つ残る ) sp 混成 : 直線形 (p 軌道が つ残る ) 多重結合との関係炭素などでは以下が基本 ( たまに違う ) 二重結合 sp 混成三重結合 sp 混成 逆に,

